- Страницы работы
- Содержание работы
- Сущность и характеристика метода покоординатного спуска (метод Гаусса-Зейделя). Геометрическая интерпретация метода покоординатного спуска для целевой функции z=(x,y). Блок-схема и алгоритм для написания программы для оптимизации методом Хука-Дживса.
- Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
- Подобные документы
Классификация методов оптимизации
Совершенствование металлургических процессов чаще всего связано с определением экстремальных значений технико-экономических показателей.
Экстремум (от лат. extremum – край, конец) – наибольшее или наименьшее значение какой-либо функции.
Цель таких исследований – поиск оптимальных условий технологических процессов, составов сплавов, конструкций.
Оптимизация (от лат. optimus – наилучший) – математическая процедура отыскания наивыгоднейших характеристик какой-либо системы.
По количеству априорной (доопытной) информации об исследуемом процессе оптимизация бывает экспериментальная, когда неизвестна связь факторов с параметром оптимизации, и теоретическая, когда имеется математическая модель процесса. К экспериментальным методам относятся все шаговые методы (Бокса-Уилсона, ПСМ, Гаусса-Зейделя и др.), к теоретическим – математическое программирование (исследования функций, множителей Лагранжа и пр.).
По способу реализации пробных воздействий методы поиска экстремума делятся на детерминированные и случайные.
Детерминанта (от лат. determinans – определяющий) – причина, которая определяет возникновение явления.
При детерминированном поиске пробные движения осуществляются по определенному алгоритму, а направление и знаки приращений зависят от предыдущего движения, т.е. предыдущее определяет последующее.
Алгоритм (от лат. Algorithms – ал-Хорезми (узбекский математик 9 век)) – совокупность действий (правил) для решения данной задачи.
К детерминированным методам поиска экстремума относятся метод крутого восхождения, наискорейшего спуска, условного экстремума, последовательного симплексного (ПСМ) и др.
В случайных стратегиях поиска направления приращений управляющих воздействий задаются случайным образом, причем все направления равновероятны, а движение к экстремуму осуществляется в том случае, когда результат приводит к улучшению параметра оптимизации. К этим методам относятся случайный перебор всех возможных значений, чисто случайный поиск, Гаусса-Зейделя, статистический градиент и пр.
В качестве примера экспериментальной оптимизации рассмотрим самый простейший – метод Гаусса-Зейделя, а теоретической – метод исследования функций.
Оптимум процесса по этому методу определяется поочередным варьированием каждого фактора при фиксированном значении других. Последовательность операций следующая:
§ выбирают шаг варьирования каждого фактора (примерно 10% области определения фактора),
§ выбирается нулевая (стартовая) точка (нулевая точка выбирается таким образом, чтобы значения факторов были близки к обычным, чаще всего применяемым),
§ производятся пробные эксперименты с изменением значения каждого из факторов, сравниваются значения параметров оптимизации и по изменению его в лучшую сторону намечается фактор и направление последующих экспериментов,
§ производятся следующие эксперименты до тез пор, пока значение параметра не будет ухудшаться,
§ возвращаются к условиям опыта с лучшим значением параметра, изменяют второй фактор и проводят опыты до ухудшения.
Процедура повторяется до тех пор, пока не будет найден экстремум параметра оптимизации или последний будет ограничен границами факторного пространства.
Пример. Методом Гаусса-Зейделя выбрать оптимальные значения массы подачи (М) и количества прямых подач (А) для доменной печи полезным объёмом 2000 м 3 (см. пример п.п. 5.2, 5.3).
В качестве целевого параметра оптимизации выберем использование газового потока hсо = 100* СО2 /(СО2+СО). Количество прямых подач может меняться от 50 до 100%, поэтому шаг варьирования выбираем, в соответствии с рекомендацией (10-20% от области определения фактора), 10 %. Масса подачи для печей такого объёма изменяется, в зависимости от качества сырья, от 25 до 30 т, следовательно, шаг по этому фактору будет 1,0 т. Нулевая (стартовая) точка соответствует параметрам обычной работы печи, т.е. М = 26 т, А = 60%. Взаимно корреляционные функции (М, А ®hсо) показали, что время одного эксперимента на печи составляет не менее двух часов.
Итак, проводим двухчасовой эксперимент на печи с массой подачи 26 т и количеством прямых подач 60%, регистрируем использование газового потока hсо = 41% по анализу общего колошникового газа и заносим в табл.6.1.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9507 –  | 7341 –
| 7341 –  или читать все.
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Страницы работы


Содержание работы
Тема 7: Методы поисковой оптимизации
Главной целью большинства исследований является достижение наилучших показателей (при разработке рецептуры материала, технологии процесса и т. д.).
Оптимизацией называется процесс нахождения наилучших значений целевой функции y (критерия оптимизации).
Если критерий оптимизации у есть функция входных управляемых параметров x1, x2. xn :
где n- число факторов, то задача оптимизации сводится к отысканию таких значений факторов
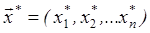 ,
,
при которых целевая функция у достигает экстремума (минимума или максимума).
Решение, т.е. отыскание вектора 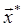 может быть аналитическим (1) и экспериментальным (2).
может быть аналитическим (1) и экспериментальным (2).
(1). В случае, когда целевая функция у задана используют известное свойство функций, имеющих экстремум, а именно, в точке экстремума первая производная этой функции обращается в ноль. Таким образом, для n-факторного пространства, чтобы найти вектор 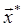 , находят n частных производных по каждому из n-факторов и решают систему уравнений:
, находят n частных производных по каждому из n-факторов и решают систему уравнений:
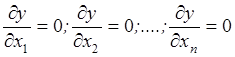
(2). В случае, когда целевая функция у неизвестна используют экспериментальные методы поисковой оптимизации, основными из которых являются:
а) метод Гаусса-Зайделя;
б) метод градиента;
в) метод крутого восхождения Бокса-Уилсона;
г) симплексный метод.
Каждый из методов включает в себя 2 процедуры:
(а) определение направления движения к экстремуму с помощью пробных опытов;
(б) «рабочее» движение в сторону экстремума.
Метод Гаусса-Зайделя предусматривает поочерёдное нахождение частных экстремумов целевой функции по каждому фактору xi ( i=1,2,…,n ). При этом на каждом i-м этапе стабилизируют n-1 факторов и варьируют только один i-й фактор.
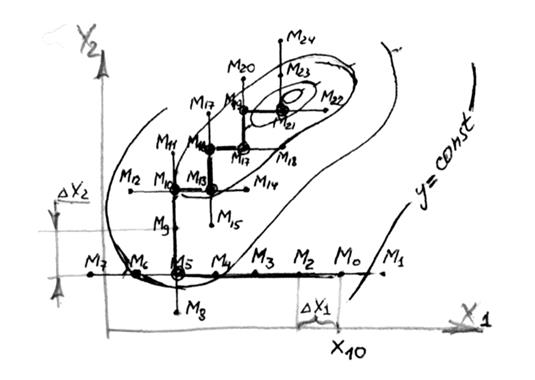
Рис. Метод Гаусса-Зайделя
Графическая интерпретация метода дана на рисунке на примере двух факторов x1 и x2 . Функция отклика у изображена топографическим способом с помощью замкнутых линий постоянного уровня у (у=const).
До начала исследований форма функции отклика, естественно, неизвестна, т. е. исследователь на момент планирования не видит этих линий. (Они видны на рисунке, чтобы понять как работает метод). Путь движения обозначен точками М. Задачу поиска максимума решают в несколько этапов:
Этап I: Поиск частного экстремума при движении по х1 со стабилизацией всех остальных факторов.
(чаще в центре области исследования)
1.2 Выбор интервала варьирования 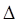 х1 по фактору х1. Размер
х1 по фактору х1. Размер 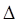 х1 определяет скорость движения к экстремуму.
х1 определяет скорость движения к экстремуму.
1.3 Определение координаты пробных точек М1 (х10+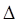 х1; х20;…; хn0) и М2(х10–
х1; х20;…; хn0) и М2(х10–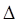 х1; х20;…;хn0).
х1; х20;…;хn0).
1.4 Определение у(М1) и у(М2) в результате проведения пробных опытов.
1.5 Определение направления движения в сторону большего у(Мi): например, если у(М2)> у(М1), то рабочее движение совершают на один шаг по направлению вектора 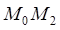 в точку М3.
в точку М3.
1.6 Продолжение движения аналогичным образом продолжается до реализации условия у(Мк) 1 2
Сущность и характеристика метода покоординатного спуска (метод Гаусса-Зейделя). Геометрическая интерпретация метода покоординатного спуска для целевой функции z=(x,y). Блок-схема и алгоритм для написания программы для оптимизации методом Хука-Дживса.
| Рубрика | Математика |
| Предмет | Методы оптимизации |
| Вид | контрольная работа |
| Язык | русский |
| Прислал(а) | incognito |
| Дата добавления | 26.12.2012 |
| Размер файла | 878,3 K |

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Подобные документы
Общая схема методов спуска. Метод покоординатного спуска. Минимизация целевой функции по выбранным переменным. Алгоритм метода Гаусса-Зейделя. Понятие градиента функции. Суть метода наискорейшего спуска. Программа решения задачи дискретной оптимизации.
курсовая работа [90,8 K], добавлен 30.04.2011
Поиск оптимального решения. Простейший способ исключения ограничений. Многомерные методы оптимизации, основанные на вычислении целевой функции. Метод покоординатного спуска. Модифицированный метод Хука-Дживса. Исследование на минимум функции Розенброка.
курсовая работа [697,6 K], добавлен 21.11.2012
Методы нахождения минимума функций градиентным методом наискорейшего спуска. Моделирование метода и нахождение минимума функции двух переменных с помощью ЭВМ. Алгоритм программы, отражение в ней этапов метода на языке программирования Borland Delphi 7.
лабораторная работа [533,9 K], добавлен 26.04.2014
Формирование функции Лагранжа, условия Куна и Таккера. Численные методы оптимизации и блок-схемы. Применение методов штрафных функций, внешней точки, покоординатного спуска, сопряженных градиентов для сведения задач условной оптимизации к безусловной.
курсовая работа [1,8 M], добавлен 27.11.2012
Численные методы поиска безусловного экстремума. Задачи безусловной минимизации. Расчет минимума функции методом покоординатного спуска. Решение задач линейного программирования графическим и симплексным методом. Работа с программой MathCAD.
курсовая работа [517,9 K], добавлен 30.04.2011
Методы нахождения минимума функции одной переменной и функции многих переменных. Разработка программного обеспечения вычисления локального минимума функции Химмельблау методом покоординатного спуска. Поиск минимума функции методом золотого сечения.
курсовая работа [95,1 K], добавлен 12.10.2009
Рассмотрение эффективности применения методов штрафов, безусловной оптимизации, сопряженных направлений и наискорейшего градиентного спуска для решения задачи поиска экстремума (максимума) функции нескольких переменных при наличии ограничения равенства.
контрольная работа [1,4 M], добавлен 16.08.2010
Понятие и специфические черты системы линейных алгебраических уравнений. Механизм и этапы решения системы линейных алгебраических уравнений. Сущность метода исключения Гаусса, примеры решения СЛАУ данным методом. Преимущества и недостатки метода Гаусса.
контрольная работа [397,2 K], добавлен 13.12.2010
Форма для ввода целевой функции и ограничений. Характеристика симплекс-метода. Процесс решения задачи линейного программирования. Математическое описание алгоритма симплекс-метода. Решение задачи ручным способом. Описание схемы алгоритма программы.
контрольная работа [66,3 K], добавлен 06.04.2012
Геометрическая интерпретация методов Ньютона, итерации и спуска. Определение корня уравнения с заданной степенью точности. Решение систем нелинейных алгебраических уравнений. Нахождение эквивалентного преобразования для выполнения условия сходимости.
курсовая работа [371,6 K], добавлен 14.01.2015
