Доброго времени суток! В этой статье мы поговорим о решении систем нелинейных алгебраических уравнений в Matlab. Вслед за решением нелинейных уравнений, переходим к их системам, рассмотрим несколько методов реализации в Matlab.
Общая информация
Итак, в прошлой статье мы рассмотрели нелинейные уравнения и теперь необходимо решить системы таких уравнений. Система представляет собой набор нелинейных уравнений (их может быть два или более), для которых иногда возможно найти решение, которое будет подходить ко всем уравнениям в системе.

В стандартном виде, количество неизвестных переменных равно количеству уравнений в системе. Необходимо найти набор неизвестных переменных, которые при подставлении в уравнения будут приближать значение уравнения к 0. Иногда таких наборов может быть несколько, даже бесконечно много, а иногда решений не существует.
Чтобы решить СНАУ, необходимо воспользоваться итеративными методами. Это методы, которые за определенное количество шагов получают решение с определенной точностью. Также очень важно при решении задать достаточно близкое начальное приближение, то есть такой набор переменных, которые близки к решению. Если решается система из 2 уравнений, то приближение находится с помощью построение графика двух функций.
Далее, мы рассмотрим стандартный оператор Matlab для решения систем нелинейных алгебраических уравнений, а также напишем метод простых итераций и метод Ньютона.
Оператор Matlab для решения СНАУ
В среде Matlab существует оператор fsolve, который позволяет решить систему нелинейных уравнений. Сразу рассмотрим задачу, которую, забегая вперед, решим и другими методами для проверки.
Решить систему нелинейных уравнений с точность 10 -2 :
cos(x-1) + y = 0.5
x-cos(y) = 3
Нам дана система из 2 нелинейных уравнений и сначала лучше всего построить график. Воспользуемся командой ezplot в Matlab, только не забудем преобразовать уравнения к стандартному виду, где правая часть равна 0:
Функция ezplot строит график, принимая символьную запись уравнения, а для задания цвета и толщины линии воспользуемся функцией set. Посмотрим на вывод:

Как видно из графика, есть одно пересечение функций — то есть одно единственное решение данной системы нелинейных уравнений. И, как было сказано, по графику найдем приближение. Возьмем его как (3.0, 1.0). Теперь найдем решение с его помощью:
Создадим функцию m-файлом fun.m и поместим туда следующий код:
Заметьте, что эта функция принимает вектор приближений и возвращает вектор значений функции. То есть, вместо x здесь x(1), а вместо y — x(2). Это необходимо, потому что fsolve работает с векторами, а не с отдельными переменными.
И наконец, допишем функцию fsolve к коду построения графика таким образом:
Таким образом у нас образуется два m-файла. Первый строит график и вызывает функцию fsolve, а второй необходим для расчета самих значений функций. Если вы что-то не поняли, то в конце статьи будут исходники.
И в конце, приведем результаты:
xr (это вектор решений) =
3.3559 1.2069
fr (это значения функций при таких xr, они должны быть близки к 0) =
1.0e-09 *
0.5420 0.6829
ex (параметр сходимости, если он равен 1, то все сошлось) =
1
И, как же без графика с ответом:

Метод простых итераций в Matlab для решения СНАУ
Теперь переходим к методам, которые запрограммируем сами. Первый из них — метод простых итераций. Он заключается в том, что итеративно приближается к решению, конечно же, с заданной точностью. Алгоритм метода достаточно прост:
- Если возможно, строим график.
- Из каждого уравнения выражаем неизвестную переменную след. образом: из 1 уравнения выражаем x1, из второго — x2, и т.д.
- Выбираем начальное приближение X0, например (3.0 1.0)
- Рассчитываем значение x1, x2. xn, которые получили на шаге 2, подставив значения из приближения X0.
- Проверяем условие сходимости, (X-X0) должно быть меньше точности
- Если 5 пункт не выполнился, то повторяем 4 пункт.
И перейдем к практике, тут станет все понятнее.
Решить систему нелинейных уравнений методом простых итераций с точность 10 -2 :
cos(x-1) + y = 0.5
x-cos(y) = 3
График мы уже строили в предыдущем пункте, поэтому переходим к преобразованию. Увидим, что x из первого уравнения выразить сложно, поэтому поменяем местами уравнения, это не повлияет на решение:
x-cos(y) = 3
cos(x-1) + y = 0.5
Далее приведем код в Matlab:
В этой части мы выразили x1 и x2 (у нас это ‘x’ и ‘y’) и задали точность.
В этой части в цикле выполняются пункты 4-6. То есть итеративно меняются значения x и y, пока отличия от предыдущего значения не станет меньше заданной точности.
k = 10
x = 3.3587
y = 1.2088
Как видно, результаты немного отличаются от предыдущего пункта. Это связано с заданной точностью, можете попробовать поменять точность и увидите, что результаты станут такими же, как и при решении стандартным методом Matlab.
Метод Ньютона в Matlab для решения СНАУ
Решение систем нелинейных уравнений в Matlab методом Ньютона является более эффективным, чем использование метода простых итераций. Сразу же представим алгоритм, а затем перейдем к реализации.
- Если возможно, строим график.
- Выбираем начальное приближение X0, например (3.0 1.0)
- Рассчитываем матрицу Якоби w, это матрица частных производных каждого уравнения, считаем ее определитель для X0.
- Находим вектор приращений, который рассчитывается как dx = -w -1 * f(X0)
- Находим вектор решения X = X0 + dx
- Проверяем условие сходимости, (X-X0) должно быть меньше точности
Далее, решим тот же пример, что и в предыдущих пунктах. Его график мы уже строили и начальное приближение останется таким же.
Решить систему нелинейных уравнений методом Ньютона с точность 10 -2 :
cos(x-1) + y = 0.5
x-cos(y) = 3
Перейдем к коду:
Сначала зададим начальное приближение. Затем необходимо просчитать матрицу Якоби, то есть частные производные по всем переменным. Воспользуемся символьным дифференцированием в Matlab, а именно командой diff с использованием символьных переменных.
Далее, сделаем первую итерацию метода, чтобы получить вектор выходных значений X, а потом уже сравнивать его с приближением в цикле.
В этой части кода выполняем первую итерацию, чтобы получить вектор решения и сравнивать его с вектором начального приближения. Отметим, чтобы посчитать значение символьной функции в Matlab, необходимо воспользоваться функцией subs. Эта функция заменяет переменную на числовое значение. Затем функция double рассчитает это числовое значение.
Все действия, которые были выполнены для расчета производных, на самом деле можно было не производить, а сразу же задать производные. Именно так мы и поступим в цикле.
В этой части кода выполняется цикл по расчету решения с заданной точностью. Еще раз отметим, что если в первой итерации до цикла были использованы функции diff, double и subs для вычисления производной в Matlab, то в самом цикле матрица якоби была явно задана этими частными производными. Это сделано, чтобы показать возможности среды Matlab.
За 3 итерации достигнут правильный результат. Также важно сказать, что иногда такие методы могут зацикливаться и не закончить расчеты. Чтобы такого не было, мы прописали проверку на количество итераций и запретили выполнение более 100 итераций.
Заключение
В этой статье мы познакомились с основными понятиями систем нелинейных алгебраических уравнений в Matlab. Рассмотрели несколько вариантов их решения, как стандартными операторами Matlab, так и запрограммированными методами простых итераций и Ньютона.
В математическом пакете MatLab имеются как программные средства для реализации алгоритмов уточнения корней уравнений, приведенных в п.6.2.2, так и встроенные функции для численного и аналитического вычисления корней уравнений.
Рассмотрим программные средства MatLabна примерах.
Пример 6.2.4-10. Локализовать корни уравнения f(x)=x 3 –cos(x)+1 средствами пакета MatLab.
 Пример 6.2.4-10 Пример 6.2.4-10 |
>> f = inline(‘x.^3 – cos(x) + 1’); >> x = linspace(-10,10,100); >> figure(‘Name’, ‘[-10,10]’); >> axes(‘NextPlot’, ‘Add’); >> grid on >> plot(x, f(x));  >> figure(‘Name’, ‘[-1,1]’); >> axes(‘NextPlot’, ‘Add’); >> grid on >> x = linspace(-1,1,100); >> plot(x, f(x)); >> figure(‘Name’, ‘[-1,1]’); >> axes(‘NextPlot’, ‘Add’); >> grid on >> x = linspace(-1,1,100); >> plot(x, f(x));  >> figure(‘Name’, ‘[-0.6,-0.4]’); >> axes(‘NextPlot’, ‘Add’); >> grid on >> x = linspace(-0.6,-0.4,100); >> plot(x, f(x)); >> figure(‘Name’, ‘[-0.6,-0.4]’); >> axes(‘NextPlot’, ‘Add’); >> grid on >> x = linspace(-0.6,-0.4,100); >> plot(x, f(x)); 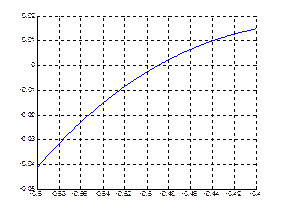 >> figure(‘Name’, ‘[-0.2,0.2]’); >> axes(‘NextPlot’, ‘Add’); >> grid on >> x = linspace(-0.2,0.2,100); >> plot(x, f(x)); >> figure(‘Name’, ‘[-0.2,0.2]’); >> axes(‘NextPlot’, ‘Add’); >> grid on >> x = linspace(-0.2,0.2,100); >> plot(x, f(x));  >> >> |
Решение алгебраических и трансцендентных уравнений в среде MatLAB проще реализовать с помощью встроенных функций: solve(), fzero(), roors().
Для нахождения вещественных корней уравнений вида f(х)=0 используется функция fzero(). Алгоритм, реализованный этой функцией, представляет собой комбинацию хорошо известного метода дихотомии (деления пополам), метода секущих и метода обратной квадратичной интерполяции. В простейшем варианте обращения кроме указателя на функцию, корень которой ищется, задается окрестность х0, с которой начинается поиск: х = fzero(f, x0).
Аргументf может быть задан одним из способов:
· как формула с неизвестным х, заключенная в апострофы;
· как имя m-файла (в апострофах и без расширения m);
· как указатель на функцию (например, @f_name);
· как указатель на анонимную функцию (например, f_handie).
Необходимо обратить внимание на то, что формула, заключенная в апострофы, в качестве независимой переменной может содержать только х. Использование независимой переменной с другим именем вызовет сообщение об ошибке.
Аргумент х0 может быть задан одним из двух способов:
· как вектор [a;b], представляющий интервал (а
Пример 6.2.4-11. Построить график функции f(x)= x∙e – x + sin(x) для локализации корня.
 Пример 6.2.4-11 Пример 6.2.4-11 |
| x = 0 : 0.1 : 2* pi; y = x.*exp(-x)+sin(x); plot(x, y) gr /> |
Из графика видно, что один из корней находится на интервале [3;4]. И этой информацией естественно воспользоваться при обращении к функции fzero( ):
 Пример 6.2.4-11 Пример 6.2.4-11 |
| >> x=fzero(‘x.*exp(-x)+sin(x)’,[3,4]) x= 3.2665 >> |
Вместо явного задания формулы для функции f мы могли бы объявить соответствующую функцию, запомнив ее в виде автономного m-файла или включив ее в качестве подфункции в файл нашей программы.
 Пример 6.2.4-11 Пример 6.2.4-11 |
| function fzerol x=fzero(@f1, [3;4]) function y=f1(z) y= z*exp(-z)+sin(z); |
Если мы хотим получить не только значение корня, но и узнать значение функции в найденной точке, то к функции fzero( ) можно обратиться с двумя выходными параметрами.
В ряде задач такая точность может оказаться излишней. MatLab предоставляет пользователю возможность формировать различные условия прекращения итерационного процесса – по точности вычисления координаты х, по модулю значения функции f(), по количеству обращений к функции f( ) и т. д.
В некоторых случаях применение функции fzero() может дать парадоксальные результаты.
Пример 6.2.4-12. Найти решения tg(x) = 0 на интервале [1;2].
 Пример 6.2.4-12 Пример 6.2.4-12 |
| >> [x,f]=fzero(‘tan(x) ‘, [1,2]) х = 1.5708 f = -1.2093e+015 >> |
Якобы «корень», соответствующий приближенному значению /2, на самом деле является точкой разрыва, при переходе через которую функция меняет знак. Выведенное значение функции в найденной точке убеждает нас в том, что найден не корень.
Функцияfzero() может возвратить еще два выходных параметра.
 Пример 6.2.4-12 Пример 6.2.4-12 |
| >> [x,f,e_flag,inform] = fzero> |
Положительное значение e_fiag (обычно, это 1) означает, что удалось найти интервал, на концах которого функция f( ) меняет знак (пример с tg(x) не должен притупить вашу бдительность). Если такой интервал не обнаружен, то e_fiag=-1. Структура inform содержит три поля с именами iterations, funcCount и algorithm. В первом из них находится количество итераций, выполненных при поиске корня, во втором – количество обращений к функции f( ), в третьем – наименование алгоритма, использованного для нахождения корня.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9622 –  | 7515 –
| 7515 –  или читать все.
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
предназначена функция fsolve.
Здесь x – вектор и F(x) – функция, которая возвращает значение вектора.
Наиболее полная информация о функции fsolve приведена в справочной системе MATLAB. Здесь приводится только краткое описание.
x = fsolve(fun,x0)
x = fsolve(fun,x0,options)
[x,fval,exitflag] = fsolve(. )
[x,fval,exitflag,output] = fsolve(. )
[x,fval,exitflag,output,jacobian] = fsolve(. )
fsolve находит корни (нули) системы нелинейных уравнений.
Таблица 4-1, Входные аргументы, содержит общее описание аргументов, передаваемых в fsolve. Данный подраздел приводит функционально-специфические детали для fun и options:
Подлежащая решению система уравнений.
fun есть такая функция, которая принимает вектор х и возвращает вектор F, нелинейные уравнения х. Функция fun может задаваться с помощью описателя функций
x = fsolve(@myfun,x0)
где myfun есть такая функция MATLAB, что
function F = myfun(x)
F = . % Расчет значений функции от x
fun так же может быть внутренним объектом.
Если к тому же может быть рассчитан Якобиан и установленная с помощью options = optimset(‘Jacobian’,’on’) опция options.Jacobian равна ‘on’, то функция fun во втором выходном аргументе должна возвращать значение Якобиана J, как матрицы от х.
Опции обеспечивают учет специфических деталей функции виде параметров options.
Таблица ниже содержат общее описание возвращаемых fsolve. аргументов. В этом разделе приводятся общие специфические детали для величин exitflag и output:
Описывает выходные условия.
- > 0 Данная функция сходится к решению по х.
- 0 Максимальное число оценки функции или итерации было превышено
- LargeScale , поскольку она устанавливает преимущественное право, какой алгоритм использовать. Это только преимущественное право, поскольку должны быть выполнены определенные условия для того, что бы можно было использовать крупно-масштабный алгоритм. Для fsolve, поскольку система нелинейных уравнений не может быть недоопределенной, число уравнений (или иначе число возвращаемых fun элементовF) должно быть, по крайней мере, длины х, в противном следует использоваться средне-масштабный алгоритм.
LargeScale. В случае установки ‘on’ используется, если это возможно, крупно-масштабный алгоритм. Для использования средне-масштабного алгоритма устанавливается значение ‘off’.
Medium-Scale и Large-Scale Algorithms . Эти параметры используются как для средне-масштабного, так и крупно-масштабного алгоритмов:
Проводится печать диагностической информации о минимизируемой функции.
Уровень отображения. ‘off’ отображение не производится, ‘iter’ отображение проводится на каждой итерации, ‘final’ (принимается по умолчанию) отображение только конечной информации.
При установке ‘on’, fsolve использует заданный пользователем Якобиан (определенный в fun), или информацию об Якобиане (при использовании JacobMult) для целевой функции. При установке ‘off’, fsolve аппроксимирует Якобиан с помощью конечных разностей.
Максимально число допустимых расчетов функции.
Максимальное число допустимых итераций.
Конечное допустимое отклонение по значению функции.
Конечное допустимое отклонение по значению х.
Large-Scale Algorithm Only . Эти параметры используются только для крупно-масштабного алгоритма
Указатель функции для функции множителей Якобиана.
В случае крупно-масштабной задачи данная функция вычисляет произведение матриц Якобиана J*Y, J’*Y или J’*(J*Y) без действительного формирования J. Такая функция имеет форму
где Jinfo и дополнительные параметры p1,p2. включают в себя используемые для расчета J*Y (или J’*Y или J’*(J*Y)) матрицы. Первый аргумент Jinfo должен быть таким же, как и возвращаемый целевой функцией fun второй аргумент.
Переменные p1,p2. есть дополнительные параметры, передаваемые в fsolve (и в fun).
fsolve (fun. options,p1,p2. )
Y есть матрица с тем же самым числом строк, что и размерность данной задачи.
flag определяет какое произведение нужно вычислять.
If flag == 0 then W = J’*(J*Y).
If flag > 0 then W = J*Y.
If flag
Примечание. ‘Jacobian’ должен быть установлен как ‘on’ для того, чтобы передать Jinfo из fun в jmfun.
В каждом случае J явно не формируется.
fsolve использует Jinfo для расчета предварительных данных.
В качестве примера смотри Нелинейную Оптимизацию с Компактной, но Структурированной Матрицей Гессе и Ограничениями Типа Равенств.
Разреженные шаблоны Якобиана для конечного дифференцирования. В случае, если в fun неразумно вычислять матрицу Якобиана J, то lsqnonlin может аппроксимировать J через заданные разреженные конечные разности и структура J — т.е. расположение не нулей – обеспечиваются как значения для JacobPattern. В наихудшем случае, когда эта структура неизвестна, можно установить JacobPattern, что бы плотная матрица и полные конечно-разностные аппроксимации вычислялись на каждой итерации (что принимается по умолчанию в случае неустановки JacobPattern). Это может быть чрезвычайно затратным для больших задач, поэтому обычно заслуживает внимания усилие по определению разреженной структуры.
Максимальное число PCG (предварительно сопряженный градиент) итераций (Смотри ниже раздел Алгоритм).
Верхняя полоса предварительной обработки для PCG. По умолчанию используется диагональная начальная подготовка (верхняя полоса из 0). Для некоторых задач увеличение полосы снижает число итераций PCG.
Конечное допустимое число итераций PCG.
Типичные значения х.
Medium-Scale Algorithm Only. Эти параметры используются только для средне-масштабного алгоритма.
Сравнение вводимых пользователем производных (Якобиана) с конечноразностными производными.
Максимальное изменение в переменных для конечных-разностей.
Минимальное изменение в переменных для конечных-разностей.
Выбор алгоритма Левенберга-Макуарда вместо Гаусса-Ньютона.
Выбор алгоритма линейного поиска.
Пример 1. В данном примере находятся нули для системы из двух уравнений и двух неизвестных

Таким образом, необходимо решить следующую систему уравнений от х

Начнем с точки x0 = [-5 -5].
Сперва запишем М-файл для расчета F или значений уравнений от х
function F = myfun(x)
F = [2*x(1) – x(2) – exp(-x(1));
-x(1) + 2*x(2) – exp(-x(2))];
Далее вызовем подпрограмму оптимизации
x0 = [-5; -5]; % примем начальное приближение за решение
options=optimset(‘Display’,’iter’); %Опция выходного отображения
[x,fval] = fsolve(@myfun,x0,options) % вызов оптимизатора
после 28 обращений к функциям нули будут найдены.
Оптимальность первого порядка
Оптимизация завершена успешно:
Относительное изменение значений функции меньше, чем в OPTIONS.TolFun
fval =
1.0e-008 *
-0.5320
-0.5320
Оптимизация завершена успешно:
Пример 2. Найти матрицу x, которая удовлетворяет уравнению

начнем с точки x= [1,1; 1,1].
Сперва запишем М-файл, необходимый для расчета решаемых уравнений.
function F = myfun(x)
F = x*x*x-[1,2;3,4];
Далее запустим подпрограмму оптимизации
x0 = ones(2,2); % примем начальное приближение за решение
options = optimset(‘Display’,’off’); % Выключим отображение
[x,Fval,exitflag] = fsolve(@myfun,x0,options)
x =
-0.1291 0.8602
1.2903 1.1612
Fval =
1.0e-03 *
0.1541 -0.1163
0.0109 -0.0243
и остаток будет близок к нулю.
sum(sum(Fval.*Fval))
ans =
3.7974e-008
Данный метод основан на алгоритме метода нелинейных среднеквадратичных отклонений, используемого в lsqnonlin. Достоинство используемого метода среднеквадратичных отклонений состоит в том, что данная система уравнений не равна нулю вследствие малых погрешностей и поэтому алгоритм приходит в точку с малым остатком. Однако, если Якобиан системы является вырожденным, то алгоритм может сходиться в точку, не являющуюся решением системы уравнений (Смотри ниже Ограничения и Диагностика).
Крупно-масштабная оптимизация. По умолчанию fsolve выберет крупно-масштабный алгоритм. Данный алгоритм является реализацией метода доверительных подпространств и основан на методе внутренних отражений Ньютона, описанного в [1], [2]. Каждая итерация включает в себя приближенное решение крупной линейной системы с помощью метода предварительно сопряженных градиентов(PCG).
Средне-масштабная оптимизация. fsolve при установке options.LargeScale как ‘off’ использует метод Гаусса-Ньютона [3] с линейным поиском. В качестве альтернативы может быть выбран метод Левенберга-Макуарда [4], [5], [6] с линейным поиском. Выбор алгоритма проводится при помощи установки опции options.LevenbergMarquardt. Установка options.LevenbergMarquardt как ‘on’ (и опции options.LargeScale как ‘off’) выбирается метод Левенберга-Макуарда.
Принимаемый по умолчанию алгоритм линейного поиска, т.е. опция options.LineSearchType установлена как ‘quadcubic’, обеспечивается методом смешанной квадратичной и кубической полиноминальной интерполяции и экстраполяции. Защищенный кубической полиномиальный метод может быть выбран установкой опции LineSearchType как ‘cubicpoly’. В общем случае, данный метод требует меньшего расчета функций, но большего обращения к расчету градиента. Таким образом, если градиенты приведены и могут быть вычислены без больших затрат, то метод с кубическим полиномиальным линейным поиском является предпочтительным.
fsolve может сходиться к ненулевой точке и давать следующие сообщения:
Оптимизатор затормозился в точке, которая не является минимумом.
Повторите расчет с новой начальной точки.
В этом случае снова выполните fsolve но с другой начальной точки.
- Разрешаемая функция должна быть непрерывной. В случае успеха fsolve дает только один корень. fsolve может сходиться к ненулевой точке, то в этом случае необходимо пытаться стартовать с другой точки.
- fsolve оперирует только с реальными переменными. Если х имеет комплексные значения, то эти переменные должны быть разделены на мнимую и реальные части.
