 Средние линии треугольника Средние линии треугольника |
 Средняя линия трапеции Средняя линия трапеции |
 Средние линии четырехугольников. Теорема Вариньона Средние линии четырехугольников. Теорема Вариньона |
 Средние линии тетраэдра Средние линии тетраэдра |

Средние линии треугольника
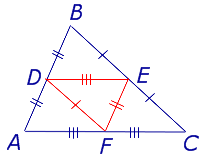
Определение . Средней линией треугольника называют отрезок, соединяющий середины двух сторон треугольника (рис. 1).
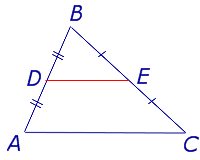
На рисунке 1 средней линией является отрезок DE .
Утверждение 1 . Средняя линия треугольника параллельна не пересекающейся с ней стороне треугольника и равна половине этой стороны.
Доказательство . Рассмотрим произвольный треугольник ABC и обозначим буквой D середину стороны AB (рис. 2). Проведем через точку D до пересечения с прямой BC прямую, параллельную прямой AC . Обозначим буквой E точку пересечения прямых DE и BC .
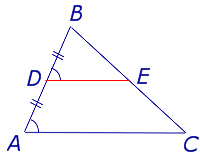
Поскольку AD = DB , а прямые AC и DE параллельны, то выполнены все условия теоремы Фалеса, и можно заключить, что выполнено равенство: CE = EB . Отсюда вытекает, что точка E является серединой стороны CB , а отрезок DE является средней линией треугольника.
Первую часть утверждения 1 мы доказали.
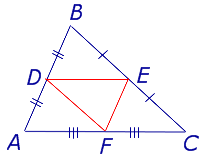
Для того, чтобы доказать вторую часть утверждения 1, заметим, что в любом треугольнике можно провести три средних линии – отрезки DE , EF и FD (рис.3).
Но поскольку AF = FC , то отсюда вытекает равенство
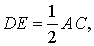
что и требуется доказать.
Доказательство утверждения 1 закончено.
- Три средних линии делят треугольник на 4 равных треугольника ADF , DBE , ECF , DEF (рис. 4).
- Каждый из четырёх треугольников ADF , DBE , ECF , DEF подобен треугольнику ABC с коэффициентом подобия 0,5 .
Средняя линия трапеции
Напомним, что трапецией трапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны.
Параллельные стороны трапеции называют основаниями , а непараллельные стороны – боковыми сторонами трапеции.
Отрезки, соединяющие противоположные вершины трапеции, называют диагоналями трапеции.
Определение . Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции (рис. 5).
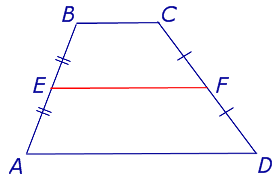
На рисунке 5 средней линией трапеции является отрезок EF .
Утверждение 2 . Средняя линия трапеции параллельна основаниям трапеции и равна половине суммы этих оснований.
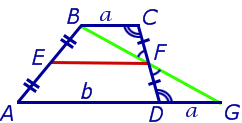
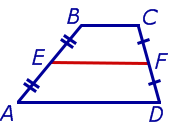
Доказательство . Проведем через вершину B и середину боковой стороны F трапеции прямую линию (рис. 6). Обозначим точку пересечения прямых BF и AD буквой G . Рассмотрим треугольники BCF и FDG . У этих треугольников стороны CF и FD равны, поскольку точка F – середина стороны CD . Углы BCF и FDG равны, поскольку они являются внутренними накрест лежащими углами, образованными при пересечении параллельных прямых BC и AD с секущей CD . Углы BFC и DFG равны, поскольку они являются вертикальными. Тем самым выполнены все условия признака равенства треугольников «По стороне и прилежащим к ней углам», и можно заключить, что треугольники BCF и FDG равны. Из равенства треугольников BCF и FDG следует равенство отрезков BF и FG , откуда вытекает, что отрезок EF является средней линией треугольника ABG . Поэтому
что и требовалось доказать.
Задача 1 . Доказать, что средняя линия трапеции делит пополам любой отрезок с концами на основаниях трапеции.
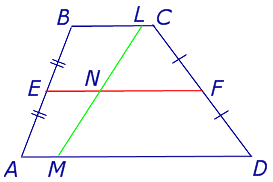
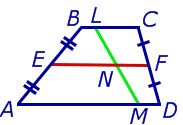
Решение . Пусть ABCD – трапеция, EF – её средняя линия, LM – указанный отрезок (рис.7). Поскольку AE = EB , то, в силу теоремы Фалеса, выполнено равенство: LN = NM , что и требовалось доказать.
Задача 2 . Доказать, что отрезок, который диагонали трапеции высекают на средней линии трапеции, равен половине разности оснований трапеции.
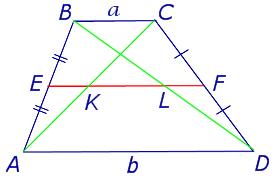
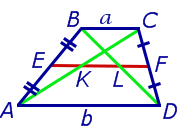
Решение . Пусть ABCD – трапеция, EF – её средняя линия, KL – указанный отрезок (рис.8). В соответствии с задачей 1 можем заключить, что точка K – середина отрезка AC , а точка L – середина отрезка BD . Поэтому отрезок EK – средняя линия треугольника BAC , а отрезок EL – средняя линия треугольника ABD . В силу утверждения 1 выполнены равенства:
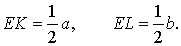
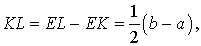
что и требовалось доказать.
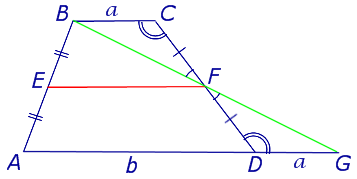
Утверждение 3 . Прямая, проходящая через середины оснований трапеции, проходит через точку пересечения боковых сторон трапеции.
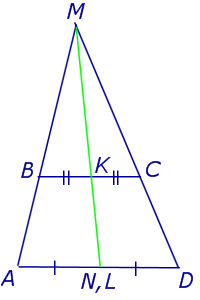
Доказательство . Пусть K и L – середины оснований BC и AD трапеции ABCD соответственно (рис.9). Обозначим буквой M точку пересечения боковых сторон AB и CD . Проведем через точки M и K прямую и обозначим точку пересечения этой прямой с основанием AD символом N . Докажем, что точки N и L совпадают. Для этого заметим, что треугольник BMK подобен треугольнику AMN . Следовательно, выполнено равенство:
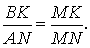
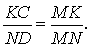
Из этих соотношений получаем:
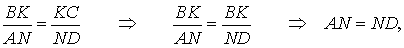
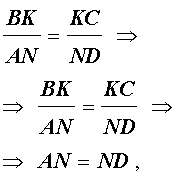
откуда вытекает, что точки N и L совпадают. Доказательство завершено.
Почти те же рассуждения позволяют доказать следующий факт, который мы предоставляем читателю в качестве упражнения.
Утверждение 4 . Прямая, проходящая через точку пересечения диагоналей и середину одного из оснований трапеции, проходит через середину другого основания трапеции.
Следствие . Точка пересечения диагоналей, середины оснований и точка пересечения боковых сторон трапеции лежат на одной прямой.
Средние линии четырехугольника. Теорема Вариньона
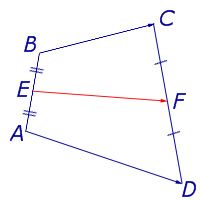
Определение . Средней линией четырехугольника называют отрезок, соединяющий середины непересекающихся сторон четырёхугольника.
Поскольку у каждого четырехугольника имеются две пары непересекающихся сторон, то у каждого четырехугольника имеются две средних линии (рис.10).
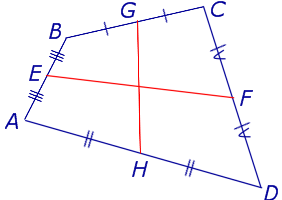
На рисунке 10 средние линии – это отрезки EF и GH .
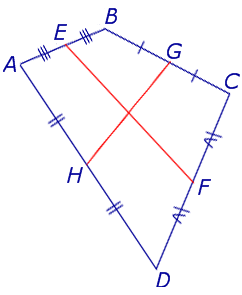
Замечание 1 . Приведенное определение средней линии относится не только к плоским четырехугольникам, но и к «пространственным четырехугольникам» (рис.11). «Пространственным четырехугольником» мы называем замкнутую ломаную линию из 4 звеньев без самопересечений, не лежащую в одной плоскости.
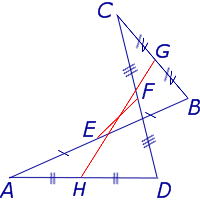
На рисунке 11 изображен «пространственный четырёхугольник» ABCD , средними линиями которого являются отрезки EF и GH .
Замечание 2 . Несмотря на то, что трапеция является четырехугольником, принято средней линией трапеции называть только отрезок, соединяющий середины её боковых сторон.
Замечание 3 . В данном разделе справочника не рассматриваются невыпуклые четырёхугольники и четырёхугольники с самопересечениями.
Теорема Вариньона . Середины сторон произвольного плоского или «пространственного» четырёхугольника являются вершинами параллелограмма параллелограмма .
Доказательство . Рассмотрим плоский четырёхугольник ABCD , изображенный на рисунке 12. Точки E, G, F, H – середины сторон, отрезок AC – диагональ четырёхугольника.
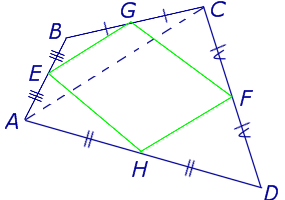
Поскольку отрезок EG – средняя линия треугольника ABC , то отрезок EG параллелен диагонали AC и равен её половине. Поскольку отрезок FH – средняя линия треугольника CDA , то отрезок FH параллелен диагонали AC и равен её половине. Таким образом, в четырёхугольнике EGFH противоположные стороны EG и FH равны и параллельны. В силу признака параллелограмма признака параллелограмма признака параллелограмма отсюда вытекает, что четырёхугольник EGFH – параллелограмм, что и требовалось доказать.
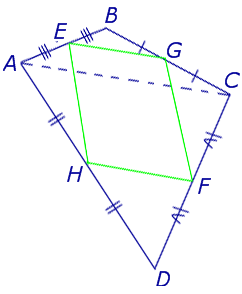
Замечание 4 . В случае «пространственного четырёхугольника» ABCD доказательство остаётся тем же (рис. 13).
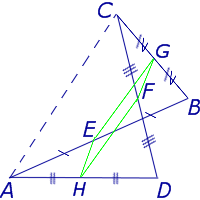
Утверждение 5 . Средние линии произвольного четырёхугольника пересекаются и в точке пересечения делятся пополам (рис. 14).
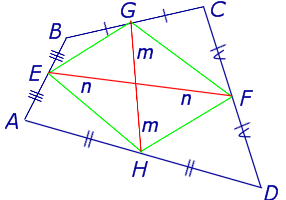
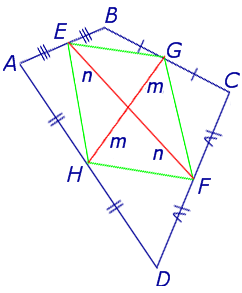
Утверждение 6 . Рассмотрим произвольный плоский или «пространственный» четырёхугольник ABCD , у которого отрезок EF является одной из средних линий (рис. 15). Тогда будет выполнено векторное равенство:
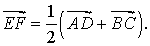
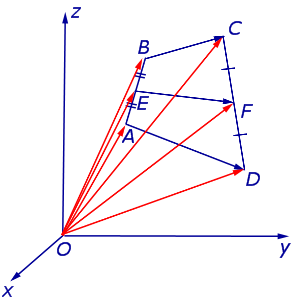
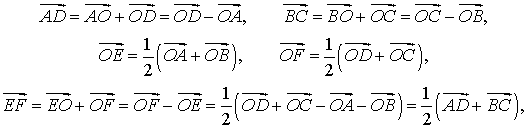
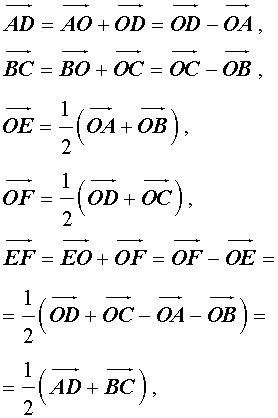
что и требовалось доказать.
Следствие . Средняя линия четырёхугольника меньше или равна половине суммы не пересекающих её сторон четырёхугольника, причём равенство достигается лишь в том случае, когда указанные стороны четырёхугольника параллельны.
Другими словами, средняя линия четырёхугольника равна половине суммы не пересекающих её сторон четырёхугольника лишь в том случае, когда этот четырехугольник является трапецией трапецией , а не пересекающие среднюю линию стороны четырёхугольника – основания трапеции.
Средние линии тетраэдра
Тетраэдром называют произвольную треугольную пирамиду (рис.17).
У каждого тетраэдра имеется 4 вершины, 4 грани и 6 рёбер, причем все рёбра делятся на 3 пары непересекающихся рёбер . На рисунке 17 каждая пара непересекающихся рёбер выделена отдельным цветом. Каждые два непересекающихся ребра тетраэдра лежат на скрещивающихся прямых скрещивающихся прямых .
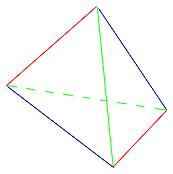
Определение . Средней линией (бимедианой) тетраэдра называют отрезок, соединяющий середины двух непересекающихся рёбер тетраэдра.
У каждого тетраэдра имеется 3 средних линии. Изображённый на рисунке 18 отрезок EF является одной из средних линий тетраэдра.
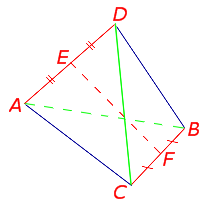
Утверждение 7 . Все средние линии тетраэдра пересекаются в одной точке и делятся этой точкой пополам.
Доказательство . Выберем какую-нибудь среднюю линию тетраэдра, например, EF и докажем, что любая другая средняя линия тетраэдра проходит через середину отрезка EF . Для этого рассмотрим, например, среднюю линию GH , соединяющую середины рёбер AC и BD , и соединим отрезками точки E, H, F, G (рис.19).
Заметим, что отрезок EH является средней линией треугольника ADB , поэтому
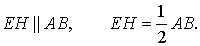
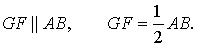
Определение . Точку пересечения средних линий тетраэдра называют центроидом тетраэдра .
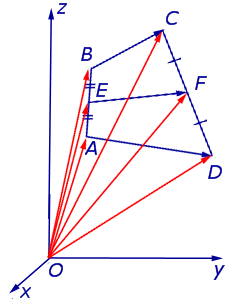
Утверждение 8 . Рассмотрим в пространстве декартову систему координат с началом в точке O и произвольный тетраэдр ABCD . Если обозначить буквой M центроид этого тетраэдра (рис. 20), то будет выполнено векторное равенство:
Что ты хочешь узнать?
Ответ
Проверено экспертом

КМ – средняя линия основания.
SAKM – отсеченная пирамида.
Vsabc = 1/3 Sabc · h
Vsakm = 1/3 Sakm · h, так как эти пирамиды имеют общую высоту.
Рассмотрим треугольники АВС и АКМ:
угол при вершине А общий, значит треугольники подобны по двум пропорциональным сторонам и углу между ними.
Площади подобных треугольников относятся как квадрат коэффициента подобия:
Sakm : S abc = 1 : 4
Vsakm = 1/3 · 1/4 Sabc · h = 1/4 (1/3 Sabc · h) = 1/4 Vsabc
Vsakm = 1/4 · 12 = 3
Определение
Пирамида – это многогранник, составленный из многоугольника (A_1A_2. A_n) и (n) треугольников с общей вершиной (P) (не лежащей в плоскости многоугольника) и противолежащими ей сторонами, совпадающими со сторонами многоугольника.
Обозначение: (PA_1A_2. A_n) .
Пример: пятиугольная пирамида (PA_1A_2A_3A_4A_5) .
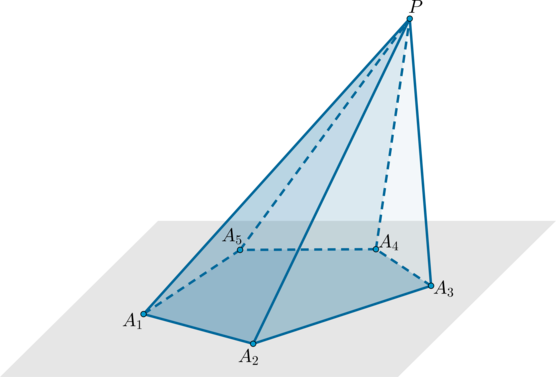
Треугольники (PA_1A_2, PA_2A_3) и т.д. называются боковыми гранями пирамиды, отрезки (PA_1, PA_2) и т.д. – боковыми ребрами, многоугольник (A_1A_2A_3A_4A_5) – основанием, точка (P) – вершиной.
Высота пирамиды – это перпендикуляр, опущенный из вершины пирамиды на плоскость основания.
Пирамида, в основании которой лежит треугольник, называется тетраэдром.
Пирамида называется правильной, если в ее основании лежит правильный многоугольник и выполнено одно из условий:
((a)) боковые ребра пирамиды равны;
((b)) высота пирамиды проходит через центр описанной около основания окружности;
((c)) боковые ребра наклонены к плоскости основания под одинаковым углом.
((d)) боковые грани наклонены к плоскости основания под одинаковым углом.
Правильный тетраэдр – это треугольная пирамида, все грани которой – равные равносторонние треугольники.
Теорема
Условия ((a), (b), (c), (d)) эквивалентны.
Доказательство
Проведем высоту пирамиды (PH) . Пусть (alpha) – плоскость основания пирамиды.
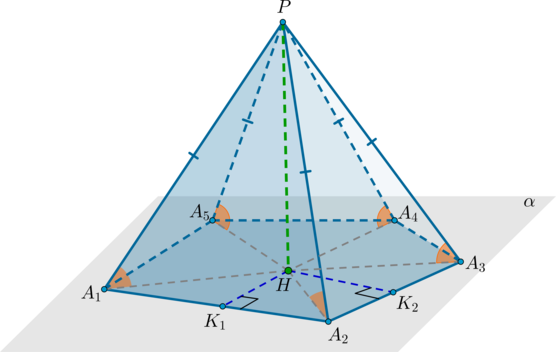
1) Докажем, что из ((a)) следует ((b)) . Пусть (PA_1=PA_2=PA_3=. =PA_n) .
Т.к. (PHperp alpha) , то (PH) перпендикулярна любой прямой, лежащей в этой плоскости, значит, треугольники (PA_1H, PA_2H, PA_3H. PA_nH) – прямоугольные. Значит, эти треугольники равны по общему катету (PH) и гипотенузам (PA_1=PA_2=PA_3=. =PA_n) . Значит, (A_1H=A_2H=. =A_nH) . Значит, точки (A_1, A_2, . A_n) находятся на одинаковом расстоянии от точки (H) , следовательно, лежат на одной окружности с радиусом (A_1H) . Эта окружность по определению и есть описанная около многоугольника (A_1A_2. A_n) .
2) Докажем, что из ((b)) следует ((c)) .
Аналогично первому пункту треугольники (PA_1H, PA_2H, PA_3H. PA_nH) прямоугольные и равны по двум катетам. Значит, равны и их углы, следовательно, (angle PA_1H=angle PA_2H=. =angle PA_nH) .
3) Докажем, что из ((c)) следует ((a)) .
Аналогично первому пункту треугольники (PA_1H, PA_2H, PA_3H. PA_nH) прямоугольные и по катету и острому углу. Значит, равны и их гипотенузы, то есть (PA_1=PA_2=PA_3=. =PA_n) .
4) Докажем, что из ((b)) следует ((d)) .
Т.к. в правильном многоугольнике совпадают центры описанной и вписанной окружности (вообще говоря, эта точка называется центром правильного многоугольника), то (H) – центр вписанной окружности. Проведем перпендикуляры из точки (H) на стороны основания: (HK_1, HK_2) и т.д. Это – радиусы вписанной окружности (по определению). Тогда по ТТП ( (PH) – перпендикуляр на плоскость, (HK_1, HK_2) и т.д. – проекции, перпендикулярные сторонам) наклонные (PK_1, PK_2) и т.д. перпендикулярны сторонам (A_1A_2, A_2A_3) и т.д. соответственно. Значит, по определению (angle PK_1H, angle PK_2H) равны углам между боковыми гранями и основанием. Т.к. треугольники (PK_1H, PK_2H, . ) равны (как прямоугольные по двум катетам), то и углы (angle PK_1H, angle PK_2H, . ) равны.
5) Докажем, что из ((d)) следует ((b)) .
Аналогично четвертому пункту треугольники (PK_1H, PK_2H, . ) равны (как прямоугольные по катету и острому углу), значит, равны отрезки (HK_1=HK_2=. =HK_n) . Значит, по определению, (H) – центр вписанной в основание окружности. Но т.к. у правильных многоугольников центры вписанной и описанной окружности совпадают, то (H) – центр описанной окружности. Чтд.
Следствие
Боковые грани правильной пирамиды – равные равнобедренные треугольники.
Определение
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой.
Апофемы всех боковых граней правильной пирамиды равны между собой и являются также медианами и биссектрисами.
Важные замечания
1. Высота правильной треугольной пирамиды падает в точку пересечения высот (или биссектрис, или медиан) основания (основание – правильный треугольник).
2. Высота правильной четырехугольной пирамиды падает в точку пересечения диагоналей основания (основание – квадрат).
3. Высота правильной шестиугольной пирамиды падает в точку пересечения диагоналей основания (основание – правильный шестиугольник).
4. Высота пирамиды перпендикулярна любой прямой, лежащей в основании.
Определение
Пирамида называется прямоугольной, если одно ее боковое ребро перпендикулярно плоскости основания.
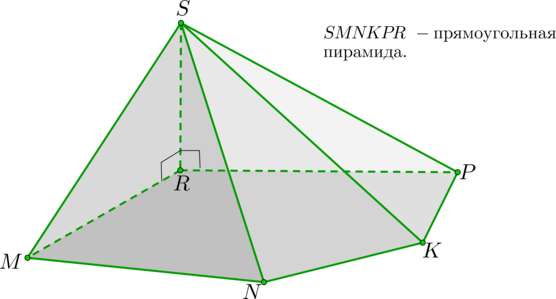
Важные замечания
1. У прямоугольной пирамиды ребро, перпендикулярное основанию, является высотой пирамиды. То есть (SR) – высота.
2. Т.к. (SR) перпендикулярно любой прямой из основания, то ( riangle SRM, riangle SRP) – прямоугольные треугольники.
3. Треугольники ( riangle SRN, riangle SRK) – тоже прямоугольные.
То есть любой треугольник, образованный этим ребром и диагональю, выходящей из вершины этого ребра, лежащей в основании, будет прямоугольным.
Теорема
Объем пирамиды равен трети произведения площади основания на высоту пирамиды: [V_< ext<пирамиды>>=dfrac13 S_< ext<осн>>cdot h]
Следствия
Пусть (a) – сторона основания, (h) – высота пирамиды.
1. Объем правильной треугольной пирамиды равен (V_< ext<прав.треуг.пир.>>=dfrac
2. Объем правильной четырехугольной пирамиды равен (V_< ext<прав.четыр.пир.>>=dfrac13a^2h) .
3. Объем правильной шестиугольной пирамиды равен (V_< ext<прав.шест.пир.>>=dfrac
4. Объем правильного тетраэдра равен (V_< ext<прав.тетр.>>=dfrac
Теорема
Площадь боковой поверхности правильной пирамиды равна полупроизведению периметра основания на апофему.
Определение
Рассмотрим произвольную пирамиду (PA_1A_2A_3. A_n) . Проведем через некоторую точку, лежащую на боковом ребре пирамиды, плоскость параллельно основанию пирамиды. Данная плоскость разобьет пирамиду на два многогранника, один из которых – пирамида ( (PB_1B_2. B_n) ), а другой называется усеченная пирамида ( (A_1A_2. A_nB_1B_2. B_n) ).
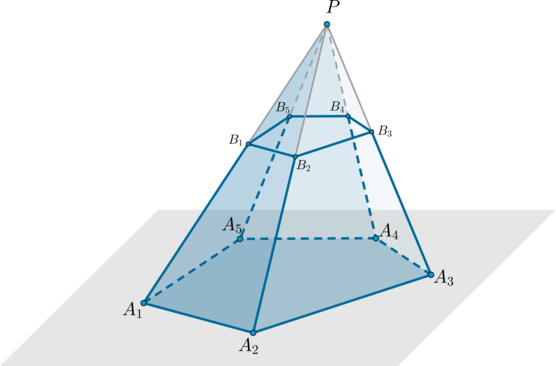
Усеченная пирамида имеет два основания – многоугольники (A_1A_2. A_n) и (B_1B_2. B_n) , которые подобны друг другу.
Высота усеченной пирамиды – это перпендикуляр, проведенный из какой-нибудь точки верхнего основания к плоскости нижнего основания.
Важные замечания
1. Все боковые грани усеченной пирамиды – трапеции.
2. Отрезок, соединяющий центры оснований правильной усеченной пирамиды (то есть пирамиды, полученной сечением правильной пирамиды), является высотой.
