Разложить в ряд фурье по синусам примеры

Ряд Фурье. Разложение функции в ряд Фурье. Разложение функции в ряд синусов и косинусов.

Ряд Фурье периодических функций с периодом 2π.	Ряд Фурье непериодических функций с периодом 2π.
Четные и нечетные функции.	Разложение в ряд Фурье по косинусам.
Разложение в ряд Фурье по синусам.	Ряд Фурье на полупериоде.
Ряд Фурье для произвольного интервала.	Ряд Фурье на полупериоде для функций, заданных на интервале L≠2π.

Ряд Фурье периодических функций с периодом 2π.

Ряд Фурье позволяет изучать периодические (непериодические) функции, разлагая их на компоненты. Переменные токи и напряжения, смещения, скорость и ускорение кривошипно-шатунных механизмов и акустические волны – это типичные практические примеры применения периодических функций в инженерных расчетах.

Разложение в ряд Фурье основывается на предположении, что все имеющие практическое значение функции в интервале -π ≤x≤ π можно выразить в виде сходящихся тригонометрических рядов (ряд считается сходящимся, если сходится последовательность частичных сумм, составленных из его членов):

Стандартная (=обычная) запись через сумму sinx и cosx

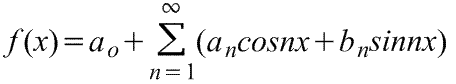(1)

Где для диапазона от -π до π коэффициенты ряда Фурье рассчитываются по формулам:

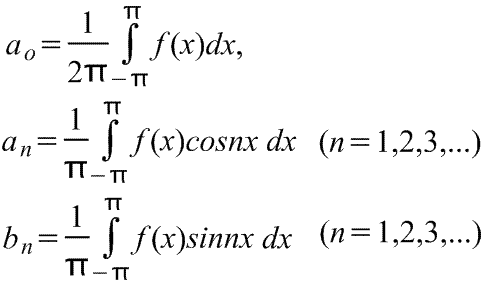
Коэффициенты a_o,a_n и b_n называются коэффициентами Фурье, и если их можно найти, то ряд (1) называется рядом Фурье, соответствующим функции f(x). Для ряда (1) член (a₁cosx+b₁sinx) называется первой или основной гармоникой,

Другой способ записи ряда – использование соотношения acosx+bsinx=csin(x+α)

Для ряда (1) член (a₁cosx+b₁sinx) или c₁sin(x+α₁) называется первой или основной гармоникой, (a₂cos2x+b₂sin2x) или c₂sin(2x+α₂) называется второй гармоникой и так далее.

Для точного представления сложного сигнала обычно требуется бесконечное количество членов. Однако во многих практических задачах достаточно рассмотреть только несколько первых членов.

Ряд Фурье непериодических функций с периодом 2π.

Разложение непериодических функций.

Если функция f(x) непериодическая, значит, она не может быть разложена в ряд Фурье для всех значений х. Однако можно определить ряд Фурье, представляющий функцию в любом диапазоне шириной 2π.

Если задана непериодическая функция, можно составить новую функцию, выбирая значения f(x) в определенном диапазоне и повторяя их вне этого диапазона с интервалом 2π. Поскольку новая функция является периодической с периодом 2π, ее можно разложить в ряд Фурье для всех значений х. Например, функция f(x)=x не является периодической. Однако, если необходимо разложить ее в ряд Фурье на интервале от о до 2π, тогда вне этого интервала строится периодическая функция с периодом 2π (как показано на рис. ниже) .

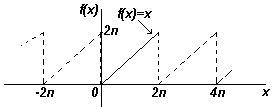
Для непериодических функций, таких как f(x)=х, сумма ряда Фурье равна значению f(x) во всех точках заданного диапазона, но она не равна f(x) для точек вне диапазона. Для нахождения ряда Фурье непериодической функции в диапазоне 2π используется все таже формула коэффициентов Фурье.

Четные и нечетные функции.

Говорят, функция y=f(x) четная, если f(-x)=f(x) для всех значений х. Графики четных функций всегда симметричны относительно оси у (т.е. являются зеркально отраженными). Два примера четных функций: у=х 2 и у=cosx.

Говорят, что функция y=f(x) нечетная, если f(-x)=-f(x) для всех значений х. Графики нечетных функций всегда симметричны относительно начала координат.

Многие функции не являются ни четными, ни нечетными.

Разложение в ряд Фурье по косинусам.

Ряд Фурье четной периодической функции f(x) с периодом 2π содержит только члены с косинусами (т.е. не содержит членов с синусами) и может включать постоянный член. Следовательно,

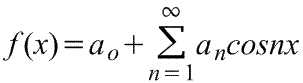
где коэффициенты ряда Фурье,

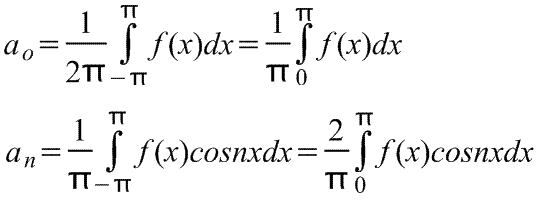
Разложение в ряд Фурье по синусам.

Ряд Фурье нечетной периодической функции f(x) с периодом 2π содержит только члены с синусами (т.е. не содержит членов с косинусами).

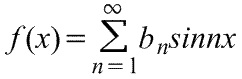
где коэффициенты ряда Фурье,

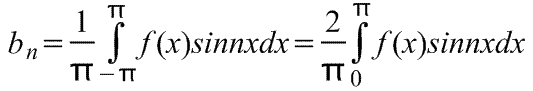
Ряд Фурье на полупериоде.

Если функция определена для диапазона, скажем от 0 до π, а не только от 0 до 2π, ее можно разложить в ряд только по синусам или тольо по косинусам. Полученный ряд Фурье называется рядом Фурье на полупериоде.

Если требуется получить разложение Фурье на полупериоде по косинусам функции f(x) в диапазоне от 0 до π, то необходимо составить четную периодическую функцию. На рис. ниже показана функция f(x)=х, построенная на интервале от х=0 до х=π. Поскольку четная функция симметрична относительно оси f(x), проводим линию АВ, как показано на рис. ниже. Если предположить, что за пределами рассмотренного интервала полученная треугольная форма является периодической с периодом 2π, то итоговый график имеет вид, показ. на рис. ниже. Поскольку требуется получить разложение Фурье по косинусам, как и ранее, вычисляем коэффициенты Фурье a_o и a_n

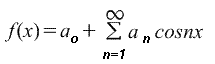
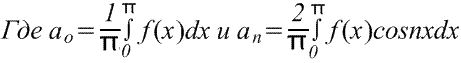
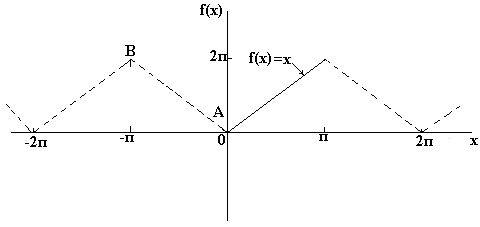
Если требуется получить разложение Фурье на полупериоде по синусам функции f(x) в диапазоне от 0 до π, то необходимо составить нечетную периодическую функцию. На рис. ниже показана функция f(x)=x, построенная на интервале от от х=0 до х=π. Поскольку нечетная функция симметрична относительно начала координат, строим линию CD, как показано на рис. Если предположить, что за пределами рассмотренного интервала полученный пилообразный сигнал является периодическим с периодом 2π, то итоговый график имеет вид, показанный на рис. Поскольку требуется получить разложение Фурие на полупериоде по синусам, как и ранее, вычисляем коэффициент Фурье. b

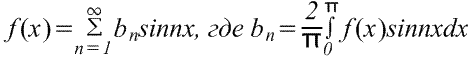
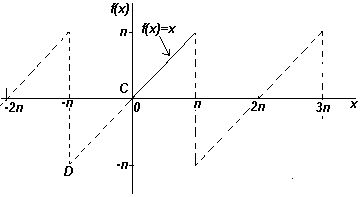
Ряд Фурье для произвольного интервала.

Разложение периодической функции с периодом L.

Периодическая функция f(x) повторяется при увеличении х на L, т.е. f(x+L)=f(x). Переход от рассмотренных ранее функций с периодом 2π к функциям с периодом L довольно прост, поскольку его можно осуществить с помощью замены переменной.

Чтобы найти ряд Фурье функции f(x) в диапазоне -L/2≤x≤L/2, введем новую переменную u таким образом, чтобы функция f(x) имела период 2π относительно u. Если u=2πх/L, то х=-L/2 при u=-π и х=L/2 при u=π. Также пусть f(x)=f(Lu/2π)=F(u). Ряд Фурье F(u) имеет вид

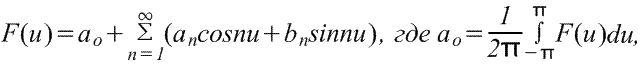
Где коэффициенты ряда Фурье,

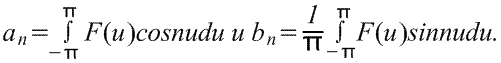
Однако чаще приведенную выше формулу приводят к зависимости от х. Поскольку u=2πх/L, значит, du=(2π/L)dx, а пределы интегрирования – от -L/2 до L/2 вместо – π до π. Следовательно, ряд Фурье для зависимости от х имеет вид

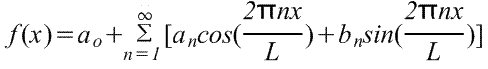
где в диапазоне от -L/2 до L/2 коэффициенты ряда Фурье,

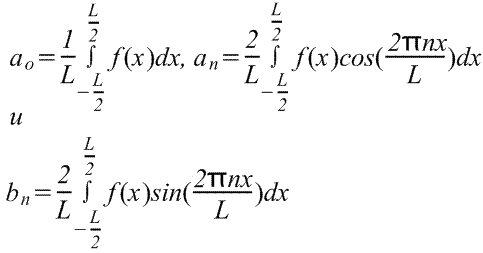
(Пределы интегрирования могут быть заменены на любой интервал длиной L, например, от 0 до L)

Ряд Фурье на полупериоде для функций, заданных в интервале L≠2π.

Для подстановки u=πх/L интервал от х=0 до х=L соответствует интервалу от u=0 до u=π. Следовательно, функцию можно разложить в ряд только по косинусам или только по синусам, т.е. в ряд Фурье на полупериоде.

Разложение по косинусам в диапазоне от 0 до L имеет вид

Понятие ряда Фурье

Тригонометрическим рядом Фурье называется ряд вида

где числа a 0 , a 1 , b 1 , a 2 , b 2 , . a n , b n , . – коэффициенты Фурье.

Более сжатая запись ряда Фурье с символом "сигма":

.

Как мы только что установили, в отличие от степенного ряда, в ряде Фурье вместо простейших функций взяты тригонометрические функции

Коэффициенты Фурье вычисляются по следующим формулам:

,

,

.

Все вышеперечисленные функции в ряде Фурье являются периодическими функциями с периодом 2π . Каждый член тригонометрического ряда Фурье является периодической функцией с периодом 2π .

Поэтому и любая частичная сумма ряда Фурье имеет период 2π . Отсюда следует, что если ряд Фурье сходится на отрезке [-π, π] , то он сходится на всей числовой прямой и его сумма, будучи пределом последовательности периодических частичных сумм, является периодической функцией с периодом 2π .

Вышеупомянутое свойство видно на графике внизу: здесь график суммы ряда для функции f(x) = x . Вне отрезка [-π, π] сумма ряда является периодическим продолжением данной функции: график функции бесконечно повторяется справа и слева.

Сходимость ряда Фурье и сумма ряда

Пусть функция F(x) , определённая на всей числовой прямой и периодическая с периодом 2π , является периодическим продолжением функции f(x) , если на отрезке [-π, π] имеет место F(x) = f(x)

Если на отрезке [-π, π] ряд Фурье сходится к функции f(x) , то он сходится на всей числовой прямой к её периодическому продолжению.

Ответ на вопрос о том, при каких условиях ряд Фурье функции f(x) сходится к этой функции, даёт следующая теорема.

Теорема. Пусть функция f(x) и её производная f ‘ (x) – непрерывные на отрезке [-π, π] или же имеют на нём конечное число точек разрыва 1-го рода. Тогда ряд Фурье функции f(x) сходится на всей числовой прямой, причём в каждой точке x , принадлежащей отрезку [-π, π] , в которой f(x) непрерывна, сумма ряда равна f(x) , а в каждой точке x 0 разрыва функции сумма ряда равна среднему арифметическому пределов функции f(x) справа и слева:

,

где и .

На концах отрезка [-π, π] сумма ряда равна среднему арифметическому значений функции в крайней левой и крайней правой точках периода разложения:

.

В любой точке x , принадлежащей отрезку [-π, π] , сумма ряда Фурье равна F(x) , если x – точка непрерывности F(x) , и равна среднему арифметическому пределов F(x) слева и справа:

,

Пример 1. Периодическая функция f(x) с периодом 2π определена следующим образом:

Проще эта функция записывается как f(x) = |x| . Разложить функцию в ряд Фурье, определить сходимость ряда и сумму ряда.

Решение. Определим коэффициенты Фурье этой функции:

Теперь у нас есть всё, чтобы получить ряд Фурье данной функции:

Этот ряд сходится во всех точках, и его сумма равна данной функции.

Решить задачу на ряды Фурье самостоятельно, а затем посмотреть решение

Пример 2. Дана периодическая функция с периодом 2π :

Определить коэффициенты Фурье.

Ряды Фурье для чётных и нечётных функций

Пусть функция f(x) определена на отрезке [-π, π] и является чётной, т. е. f(- x) = f(x) . Тогда её коэффициенты b n равны нулю. А для коэффициентов a n верны следующие формулы:

,

.

Пусть теперь функция f(x) , определённая на отрезке [-π, π] , нечётная, т.е. f(x) = – f( – x) . Тогда коэффициенты Фурье a n равны нулю, а коэффициенты b n определяется формулой

.

Как видно из формул, выведенных выше, если функция f(x) чётная, то ряд Фурье содержит только косинусы, а если нечётная, то только синусы.

Пример 3. Разложить в ряд Фурье функцию .

Решение. Это нечётная функция, поэтому её коэффициенты Фурье , а чтобы найти , нужно вычислить определённый интеграл:

Получаем ряд Фурье данной функции:

.

Это равенство справедливо для любого . В точках сумма ряда Фурье по приведённой во втором параграфе теореме не совпадает со значениями функции , а равна . Вне отрезка сумма ряда является периодическим продолжением функции , её график приводился выше в качестве иллюстрации суммы ряда.

Пример 4. Разложить в ряд Фурье функцию .

Решение. Это чётная функция, поэтому её коэффициенты Фурье , а чтобы найти , нужно вычислить определённые интегралы:

Получаем ряд Фурье данной функции:

.

Это равенство справедливо для любого , так как в точках сумма ряда Фурье в данном случае совпадает со значениями функции , поскольку .

Ряды Фурье с периодом 2l

Пусть функция f(x) определена на отрезке [– l, l] ( l – произвольное положительное число). Тогда формула ряда Фурье этой функции принимает вид

,

где коэффициенты Фурье определяются по следующим формулам:

,

,

.

Пример 5. Разложить в ряд Фурье с периодом 2l функцию f(x) , которая на отрезке [– l, l] задаётся формулой .

Решение. Это чётная функция, поэтому её коэффициент Фурье , а чтобы найти , нужно вычислить определённые интегралы:

Ряд Фурье данной функции:

.

Это равенство справедливо для любого , а это значит, что ряд сходится на всей числовой прямой.

Решить задачу на ряды Фурье самостоятельно, а затем посмотреть решение

Пример 6. Разложить в ряд Фурье с периодом 4 периодическую функцию , .

Так как функция заданана отрезке 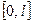,то ее можно доопределить на отрезок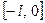четным или нечетным образом.

Если функция доопределена четным образом, то она, как четная функция может быть разложена по формулам для четной функции

, , .

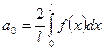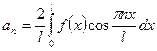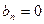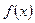
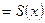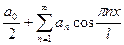= (в точках непрерывности функции).

Это – разложение в ряд Фурье по косинусам кратных дуг.

Если функция доопределена нечетным образом, то она, как нечетная функция может быть разложена по формулам для нечетной функции

, ,..

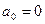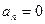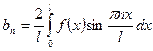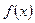
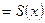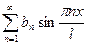= (в точках непрерывности функции).

Это – разложение в ряд Фурье по синусам кратных дуг.

Одну и ту же функцию, заданную на отрезке 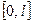,можно разложить и по синусам, и по косинусам кратных дуг.

Пример. Разложить по косинусам и синусам кратных дуг функцию 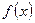, заданную на отрезке .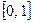

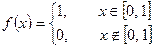Так как мы доопределяем функцию на отрезок 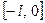при разложении по косинусам и синусам кратных дуг, то .

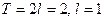Разложим функцию по косинусам кратных дуг.

, , .

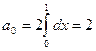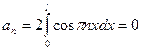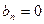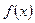
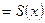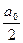==1.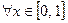

Разложим функцию по синусам кратных дуг.

, ,..

== ,

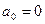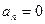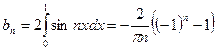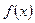
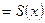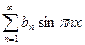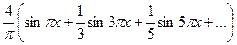
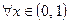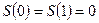(теорема Дирихле).

|	следующая лекция ==>
Свойства четных и нечетных функций	|	Комплексные числа, 3 формы записи, основные операции

Дата добавления: 2014-01-06 ; Просмотров: 5306 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет