Архимедова спираль – это кривая описываемая точкой, совершающей одновременно два равномерных движения, одно из которых, совершается вдоль радиус-вектора ρ, вращающегося вокруг полюса О, а другое – по окружности. Уравнение спирали имеет вид ρ=aφ где: R – радиус вектор; a – коэффициент пропорциональности; φ – угол поворота радиус вектора (полярный угол).
Архимедова спираль может быть построена: по уравнению ρ=aφ для чего необходимо: – определить коэффициент пропорциональности; a = ρ/φ = Rφ/(2π), где R – расстояние между двумя последовательными витками (шаг спирали); – задаться для каждой искомой точки соответственным значением угла φ; – решить уравнение ρ=aφ для принятого значения φ. Архимедова спираль имеет две ветви, одна из которых раскручивается против хода часовой стрелки и соответствует положительному значению φ, другая – по ходу часовой стрелки и соответствует отрицательному значению φ. графическим способом если заданы шаг спирали R: – из центра О описываем радиусом R окружность; – делим отрезок О-VIII, равный R и окружность на одинаковое равное число частей, например на 8. Получим на отрезке О-VIII точки 1; 2; 3 и т. д., а на окружности – I, II, III и т. д.; – из центра О прводим через точки деления окружности пучок лучей ОI, ОII, ОIII и т. д.; – из центра О описываем дуги окружностей О1, О2, О3 и т. д. до пересечения с соответствующими лучами ОI, ОII, ОIII и т. д.; – полученные точки K1; K2; K3 и т. д. соединяем плавной кривой.
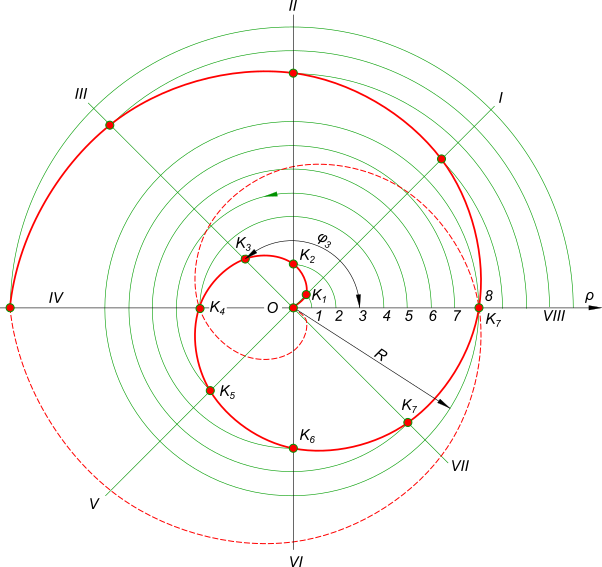
На представленном рисунке построен один виток. Если потребуется несколько удлинить виток или увеличить число витков, то для их построения необходимо использовать точки K1; K2; K3 и т. д. основного витка, отложив от каждой из этих точек на лучах ОI, ОII, ОIII и т. д. отрезок, равный шагу спирали R.
Архимедова спираль широко применяется в технике: – при конструировании фрез,
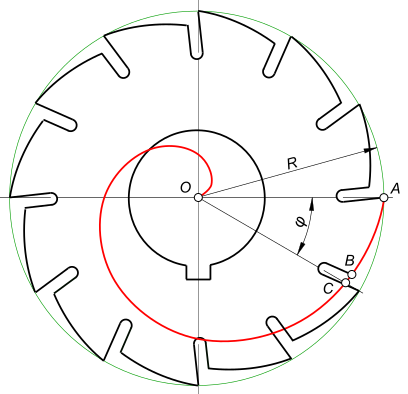
по ней выполняют затылование зубьев; – при конструировании самоцентрирующихся патронов, кулачковых механизмов,
Спиралью называется плоская кривая, описываемая точкой, удаляющейся от центра при совершении кругового движения в плоскости чертежа вокруг центра спирали. На практике различают спирали с постоянным и постепенно возрастающим расстоянием между завитками. Обычно спирали строят по точкам и вычерчивают с помощью лекала.
Для того чтобы расчертить спираль, необходимо наметить не менее двух ее центров. Если вычерчивают спираль из трех или более центров, то обычно центрами спирали являются вершины правильного треугольника или правильного многоугольника. Каждую дугу проводят из последующей вершины до пересечения с лучом из угла треугольника или многоугольника. Радиус при этом каждый раз увеличивается на длину, равную длине стороны треугольника или многоугольника.
Рассмотрим, например, как начертить так называемую «архимедову спираль» (рис. 17, а ). Для этого нужно провести горизонтальную линию и отметить на ней две точки О 1 и О 2, отстоящие одна от другой примерно на 3 мм. Поставив ножку циркуля в одну из этих точек (О 1), проведите дугу радиусом 3 мм (R 1), равную половине окружности. Концы этой дуги должны опираться на горизонтальную ось (в данном примере – сверху).
Затем перенесите ножку циркуля во вторую из отмеченных точек и увеличьте его раствор так, чтобы карандаш попал в конец первой дуги. Снова проведите половину окружности радиусом R 2, опирающуюся на горизонтальную линию, но уже с противоположной стороны (снизу). Таким же образом, переставляя ножку циркуля то в первую, то во вторую точку и каждый раз увеличивая его раствор, продолжайте разворачивать спираль. На рис. 17, а , изображено четыре полных оборота.
Для построения спирали, имеющей три центра (рис. 17, б), находящихся на равных расстояниях один от другого, необходимо предварительно построить равносторонний треугольник 1–2–3 (заштрихован) и продолжить его стороны так, как это показано на рисунке (линии 1–1’, 2–2’ и 3–3’ ).
Из центра 1 проводим дугу 3–1’ радиусом R 1, равным длине стороны треугольника, до пересечения с продолжением стороны 1–1’ . Затем из центра 2 описываем дугу радиусом R 2 = 2R 1 до пересечения с продолжением стороны 2 (линия 2–2’ ). После этого из центра 3 проводим дугу радиусом R 3 = 3R 1 до пересечения с продолжением стороны 3 (линия 3–3’ ) в точке 3’ . После этого возвращаемся в центр 1 и продолжаем построение в такой же последовательности, каждый раз увеличивая радиус дуги на величину стороны треугольника.
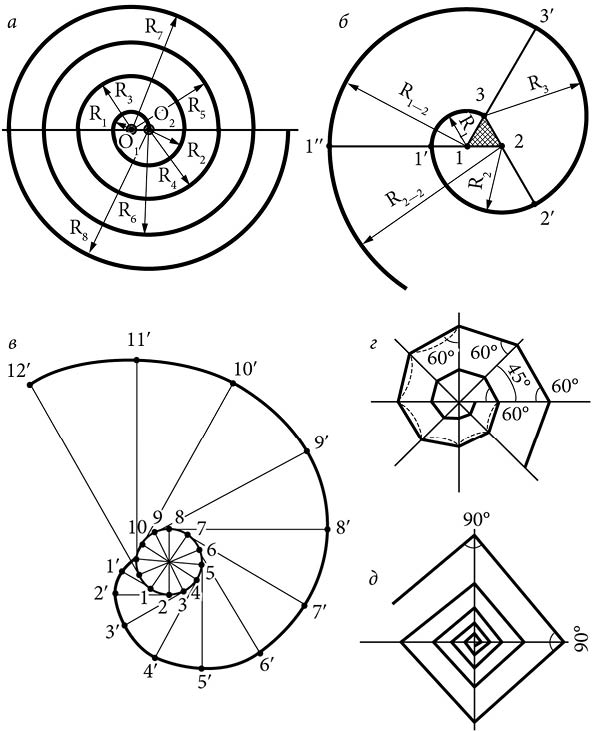
Рис. 17. Построение спиралей: а – «архимедова спираль» с двумя центрами; б – трехцентровая спираль; в – эвольвента круга; г, д – ломаные (хордовые) спирали.
Аналогично выполняют спирали с четырьмя, пятью и т. д. центрами.
Эвольвента круга (рис. 17, в ) – это плоская кривая, образуемая точкой на прямой, которая перемещается без скольжения по неподвижной окружности заданного радиуса. Эта кривая иногда называется разверткой окружности. Построение эвольвенты начинается с деления заданной окружности на произвольное число равных частей, например 12. В каждой точке деления проводим касательные к окружности. На каждой из этих касательных последовательно откладываем длину окружности, равную πd /12: в точке 1 – πd /12, в точке 2 – 2πd /12, в точке 3 – 3πd /12 и т. д. На касательной к точке 12 откладываем длину окружности, равную πd . Соединяя последовательно плавной кривой по лекалу полученные на касательных точки 1’, 2’, 3’ и т. д., получим кривую, называемую эвольвентой.
Схема построения ломаных спиралей показана на рис. 17, г, д . Они строятся так же, как и циркульные, но дуги заменяются соответствующими хордами.
Построение спирали Архимеда
Заданный шаг t спирали Архимеда делят на несколько, например на восемь, равных частей. Из конца О отрезка проводят окружность R = t и делят ее на столько же равных частей, на сколько был разделен шаг t.
На первом луче путем проведения дуги радиусом O1 из центра О получают точку I, на втором луче путем проведения дуги радиусом O2 получают точку II и т. д.
После того как на всех лучах будут получены точки I, II, III, IV, V, VI, VII и VIII, проводят через них кривую – спираль Архимеда.

Распределительный кулачок. Очертания боковых сторон его выполняют по спирали Архимеда
Уравнение Архимедовой спирали в полярной системе координат записывается так:
где k – смещение точки M по лучу r, при повороте на угол, равный одному радиану. Повороту прямой на 2 соответствует смещение a = |BM| = |MA| = 2 k. Число a – называется шагом спирали. Уравнение Архимедовой спирали можно переписать так:

При вращении луча против часовой стрелки получается правая спираль, при вращении – по часовой стрелке – левая спираль.
Обе ветви спирали (правая и левая) описываются одним уравнением:
Положительным значениям соответствует правая спираль, отрицательным – левая спираль. Если точка M будет двигаться по прямой UV из отрицательных значений через центр вращения O и далее в положительные значения, вдоль прямой UV, то точка M опишет обе ветви спирали.
Луч OV, проведенный из начальной точки O, пересекает спираль бесконечное число раз – точки B, M, A и т.д. Расстояния между точками B и M, M и A равны шагу спирали ? = 2k?. При раскручивании спирали, расстояние от точки O до точки M стремится к бесконечности, при этом шаг спирали остается постоянным (конечным), то есть чем дальше от центра, тем ближе витки спирали, по форме, приближаются к окружности.
Закон семи, или «закон октав» – закон изменения вибраций в учении Г.И. Гурджиева, изложенный П.Д. Успенским.
В своей книге Успенский говорит, что вся Вселенная состоит из вибраций. Обычно мы считаем, что они бесконечны и непрерывны, то есть начавшись, они длятся долго по восходящей или нисходящей. Но это не так. Астрология считает день – отдельной сущностью. Так и вибрации не непрерывны. Первоначальная сила вибрации действует не непрерывно, а как бы попеременно, изменяя свое качество. «Сила импульса действует, не изменяя своей природы, и вибрация развивается правильно лишь в течение некоторого времени, которое определяется природой импульса, средой, условиями и т.д. Но в известный момент в этом процессе происходит особого рода перемена, и вибрации перестают, так сказать, повиноваться импульсу, на короткое время замедляются и до известной степени меняют свою природу и направление. После этого замедления как в процессе возрастания, так и в процессе затухания вибрации возвращаются в свое прежнее русло и в течение некоторого времени возрастают или затухают однообразно – до известного момента, когда в их развитии вновь происходит задержка. В этой связи знаменательно, что периоды однообразных колебаний не равны. А периоды замедления вибраций не симметричны: один из них короче, другой длиннее».
Закон октав получил свое название за стройную организацию по нотам музыкальной октавы. Между нотами октавы первой тональности – до мажор – интервалы выстраиваются неравномерно. «До»-«ре» (большая секунда, 1 тон), «ре»-«ми» (большая секунда, 1 тон), «ми»-«фа» (малая секунда, 0,5 тона), «фа»-«соль» (большая секунда, 1 тон), «соль»-«ля» (большая секунда, 1 тон), «ля»-«си» (большая секунда, 1 тон), «си»-«до» (малая секунда, 0,5 тона).

Клавиатура, отражение «закона октав»
Беннетт формулирует это так: «Закон октав утверждает принцип, при помощи которого можно определить, будет ли тот или иной процесс завершен с сохранением изначального напряжения или нет. При этом нет никакой гарантии, что под воздействием всегда присутствующих разнообразных внешних сил удастся сохранить направление этого процесса. Нельзя так же заранее предсказать, удастся ли довести процесс до завершения, без потери формы или содержания».
