- Что такое иррациональные уравнения
- Так избавься от корней, вот и все дела!
- Решение иррациональных уравнений
- Уравнение №1
- Уравнение №2
- Уравнение №3
- А если взять не квадрат, а третью степень:
- А если показатель степени нечетный:
- Метод уединенного радикала
- Решение иррациональных уравнений включает в себя 3 шага:
- Примеры для самостоятельной работы:
- Решения примеров для самостоятельной работы:
- СРЕДНИЙ УРОВЕНЬ
- Простейшие иррациональные уравнения
- Два примера:
- Итак, общее правило:
- Реши сам:
- Ответы:
- Учет ОДЗ
- Пример №1:
- Пример №2
- Иррациональные уравнения вида √A = √B
- Как решить такое уравнение?
- Примеры (реши сам):
- Ответы:
- Иррациональные уравнения вида A√B = 0
- Примеры (реши сам):
- Ответы:
- Иррациональные уравнения вида √A=B
- Примеры:
- Ответы:
- Корни степени больше 2
- I. Корни четной степени.
- II. Корни нечетной степени.
- Где можно решить уравнение с корнями онлайн решателем?
Уравнения, в которых под знаком корня содержится переменная, называт иррациональными.
Методы решения иррациональных уравнений, как правило, основаны на возможности замены (с помощью некоторых преобразований) иррационального уравнения рациональным уравнением, которое либо эквивалентно исходному иррациональному уравнению, либо является его следствием. Чаще всего обе части уравнения возводят в одну и ту же степень. При этом получается уравнение, являющееся следствием исходного.
При решении иррациональных уравнений необходимо учитывать следующее:
1) если показатель корня – четное число, то подкоренное выражение должно быть неотрицательно; при этом значение корня также является неотрицательным (опредедение корня с четным показателем степени);
2) если показатель корня – нечетное число, то подкоренное выражение может быть любым действительным числом; в этом случае знак корня совпадает со знаком подкоренного выражения.
Пример 1. Решить уравнение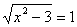
Возведем обе части уравнения в квадрат.
x 2 – 3 = 1;
Перенесем -3 из левой части уравнения в правую и выполним приведение подобных слагаемых.
x 2 = 4;
Полученное неполное квадратное уравнение имеет два корня -2 и 2.
Произведем проверку полученных корней, для этого произведем подстановку значений переменной x в исходное уравнение.
Проверка.
При x1 = -2 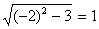 – истинно:
– истинно:
При x2 = -2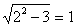 – истинно.
– истинно.
Отсюда следует, что исходное иррациональное уравнение имеет два корня -2 и 2.
Пример 2. Решить уравнение  .
.
Это уравнение можно решить по такой же методике как и в первом примере, но мы поступим иначе.
Найдем ОДЗ данного уравнения. Из определения квадратного корня следует, что в данном уравнении одновременно должны выполнятся два условия:
а) x – 9 0;
0;
x 9;
9;
б) 1 – x 0;
0;
-x -1 ;
-1 ;
x 1.
1.
ОДЗ данного уранения: x
 .
.
Ответ: корней нет.
Пример 3. Решить уравнение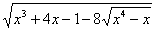 =
=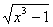 + 2
+ 2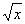 .
.
Нахождение ОДЗ в этом уравнении представляет собой достаточно трудную задачу. Возведем обе части уравнения в квадрат:
x 3 + 4x – 1 – 8 = x 3 – 1 + 4
= x 3 – 1 + 4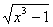

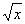 + 4x;
+ 4x;


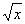 =0;
=0;
x1=1; x2=0.
Произведя проверку устанавливаем, что x2=0 лишний корень.
Ответ: x1=1.
Пример 4. Решить уравнение x =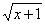 .
.
В этом примере ОДЗ найти легко. ОДЗ этого уравнения: x [-1;
[-1; ).
).
Возведем обе части этого уравнения в квадрат, в результате получим уравнение x 2 = x + 1. Корни этого уравнения:
x1 =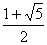
x2 =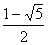
Произвести проверку найденных корней трудно. Но, несмотря на то, что оба корня принадлежат ОДЗ утверждать, что оба корня являются корнями исходного уравнения нельзя. Это приведет к ошибке. В данном случае иррациональное уравнение равносильно совокупности двух неравенств и одного уравнения:
x + 1 0 и x
0 и x 0 и x 2 = x + 1, из которой следует, что отрицательный корень для иррационального уравнения является посторонним и его нужно отбросить.
0 и x 2 = x + 1, из которой следует, что отрицательный корень для иррационального уравнения является посторонним и его нужно отбросить.
Ответ: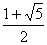
Пример 5 . Решить уравнение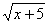 +
+ = 7.
= 7.
Возведем обе части уравнения в квадрат и выполним приведение подобных членов, перенес слагаемых из одной части равенства в другую и умножение обеих частей на 0,5. В результате мы получим уравнение
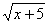

 = 12, (*) являющееся следствием исходного. Снова возведем обе части уравнения в квадрат. Получим уравнение (х + 5)(20 – х) = 144, являющееся следствием исходного. Полученное уравнение приводится к виду x 2 – 15x + 44 =0.
= 12, (*) являющееся следствием исходного. Снова возведем обе части уравнения в квадрат. Получим уравнение (х + 5)(20 – х) = 144, являющееся следствием исходного. Полученное уравнение приводится к виду x 2 – 15x + 44 =0.
Это уравнение (также являющееся следствием исходного) имеет корни x1 = 4, х2 = 11. Оба корня, как показывает проверка, удовлетворяют исходному уравнению.
Замечание. При возведении уравнений в квадрат учащиеся нередко в уравнениях типа (*) производят перемножение подкоренных выражений, т. е. вместо уравнения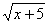 •
• = 12, пишут уравнение
= 12, пишут уравнение 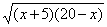 = 12. Это не приводит к ошибкам, поскольку уравнения являются следствиями уравнений. Следует, однако, иметь в виду, что в общем случае такое перемножение подкоренных выражений дает неравносильные уравнения.
= 12. Это не приводит к ошибкам, поскольку уравнения являются следствиями уравнений. Следует, однако, иметь в виду, что в общем случае такое перемножение подкоренных выражений дает неравносильные уравнения.
В рассмотренных выше примерах можно было сначала перенести один из радикалов в правую часть уравнения. Тогда в левой части уравнения останется один радикал и после возведения обеих частей уравнения в квадрат в левой части уравнения получится рациональная функция. Такой прием (уединение радикала) довольно часто применяется при решении иррациональных уравнений.
Пример 6. Решить уравнение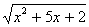 –
– = 3.
= 3.
Уединив первый радикал, получаем уравнение
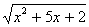 =
= + 3, равносильное исходному.
+ 3, равносильное исходному.
Возводя обе части этого уравнения в квадрат, получаем уравнение
x 2 + 5x + 2 = x 2 – 3x + 3 + 6 , равносильное уравнению
, равносильное уравнению
4x – 5 = 3 (*). Это уравнение является следствием исходного уравнения. Возводя обе части уравнения в квадрат, приходим к уравнению
(*). Это уравнение является следствием исходного уравнения. Возводя обе части уравнения в квадрат, приходим к уравнению
16x 2 – 40x + 25 = 9(x 2 – Зх + 3), или
7x 2 – 13x – 2 = 0.
Это уравнение является следствием уравнения (*) (а значит, и исходного уравнения) и имеет корни. Первый корень x1 = 2 удовлетворяет исходному уравнению, а второй x2 =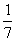 – не удовлетворяет.
– не удовлетворяет.
Заметим, что если бы мы сразу, не уединив один из радикалов, возводили обе части исходного уравнения в квадрат нам бы пришлось выполнить довольно громозкие преобразования.
При решении иррациональных уравнений, кроме уединения радикалов используют и другие методы. Рассмотрим пример использования метода замены неизвестного (метод введения вспомогательной переменной).
Пример 7. Решить уравнение 2x 2 – 6x +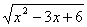 + 2 = 0.
+ 2 = 0.
Введем вспомогательную переменную. Пусть y =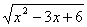 , где y
, где y 0, тогда получим уравнение 2y 2 + y – 10 = 0;
0, тогда получим уравнение 2y 2 + y – 10 = 0;
y1 = 2; y2 = –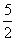 . Второй корень не удовлетворяет условию y
. Второй корень не удовлетворяет условию y 0.
0.
Возвращаемся к x:
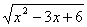 = 2;
= 2;
x 2 – 3x + 6 = 4;
x 2 -3x + 2 = 0;
x1 = 1; x2 = 2. Проверкой устанавливаем, что оба корня являются корнями иисходного уравнения.
Ответ: x1 = 1; x2 = 2.
Пример 8. Решить уравнение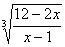 +
+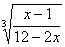 =
=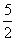
Положим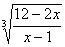 = t, Тогда уравнение примет вид t +
= t, Тогда уравнение примет вид t +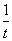 =
=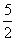 откуда получаем следствие: 2t 2 – 5t + 2 = 0 Решая это квадратное уравнение, находим два корня: t1 = 2 t2 =
откуда получаем следствие: 2t 2 – 5t + 2 = 0 Решая это квадратное уравнение, находим два корня: t1 = 2 t2 =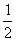 . Задача сводится теперь к решению следующих двух уравнений:
. Задача сводится теперь к решению следующих двух уравнений:
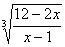 = 2,(*)
= 2,(*)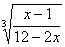 =
=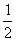 (**)
(**)
Возводя обе части уравнения (*) в куб, получаем 12 – 2x = 8x – 8; x1 = 2.
Аналогично, решив (**), находим x2 =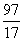 .
.
Оба найденных корня удовлетворяют исходному уравнению, так как в процессе решения мы использовали (кроме замены неизвестного) только преобразование вида [f(x) = g(x)] [f n (x) = g n (x)], а при таком преобразовании, как было отмечено выше, получается равносильное уравнение.
[f n (x) = g n (x)], а при таком преобразовании, как было отмечено выше, получается равносильное уравнение.
Ответ: х1 = 2, x2 =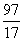 .
.
Хочешь подготовиться к ОГЭ или ЕГЭ по математике на отлично?
Хочешь проверить свои силы и узнать результат насколько ты готов к ЕГЭ или ОГЭ?
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Что такое иррациональные уравнения
Сначала разберемся что такое рациональные уравнения, а потом поймем что же из себя представляет решение иррациональных уравнений .
Итак, что такое рациональные уравнения , а что – иррациональные:
как думаешь, какое это? Тут сложение, умножение, нет корней, и степеней никаких – рациональное!
– вот тебе и корень из переменной, значит уравнение НЕ рациональное (или иррациональное);
а это – рациональное;
тут вот степень, но она с целым показателем степени ( – целое число) – значит это тоже рациональное уравнение;
даже уравнение с отрицательным показателем степени тоже является рациональным, ведь по сути – это ;
– тоже рациональное, т.к. ;
– а с ним поосторожнее, степень-то дробная, а по свойству корней , как ты помнишь корня в рациональных уравнениях не бывает. Надеюсь, теперь ты сможешь различать, к какому виду относится уравнение.
Иррациональными уравнениями называются уравнения, в которых переменная содержится под знаком корня или знаком возведения в дробную степень. А вот как это выглядит: ; .
Но только отличать рациональное от иррационального недостаточно, тебе же решать их надо! Вся сложность в корнях, так?
Так избавься от корней, вот и все дела!
Если еще не догадался как, то я подскажу – просто возведи в нужную степень обе части уравнения, а потом решай его как простое рациональное уравнение, но проверяй все корни, позже поймешь почему.
Как рациональные уравнения решать помнишь? Если забыл, то советую почитать («Рациональные уравнения»).
Если читать лень, напомню вкратце. Для верного решения рациональных уравнений, ты должен придерживаться следующего руководства:
- Понять, точно ли перед тобой рациональное уравнение (убедись, что в нем нет корней);
- Определить ОДЗ;
- Найти общий знаменатель дробей и умножить на него обе части уравнения;
- Решить получившееся целое уравнение;
- Исключить из его корней те, которые обращают в ноль знаменатель дробей.
Вроде все объяснил, давай решать, математика слов не любит.
Решение иррациональных уравнений
Уравнение №1
Вот такое вот уравнение: ,
Корень из икса видишь? Значит, какое уравнение?
Верно, оно иррациональное! Что дальше?
Избавляемся от корней, поскольку корень второй степени, то обе части уравнения возводим в квадрат и упрощаем:
Вот и все, почти все, что осталось сделать?
Правильно, решая иррациональное уравнение, обязательно надо проводить проверку полученных корней!
Подставим в исходное уравнение, именно в исходное уравнение, потому, что нам нужно найти его корни, а возведя в квадрат, мы могли получить посторонние корни (об этом позже).
Уравнение №2
О том, что это иррациональное уравнение, думаю, ты и сам знаешь. Как и раньше возводим в квадрат обе части:
Проверка, подставим в исходное уравнение:
– вот это да, ничего тебя тут не смущает? Под квадратным корнем у нас отрицательное число!
Как же так вышло?
А это говорит о том, что это посторонний корень для исходного уравнения, да, это корень уравнения , но оно-то не исходное, его мы получили после преобразований!
В ответе пишем «нет решения».
Уравнение №3
Чтобы разобраться в ситуации мы сделаем что? Будем еще решать, вот уравнение .
После возведения обеих частей в квадрат имеем:
, упрощаем и решаем квадратное уравнение по теореме Виета
У нас два корня, пробуем их подставить в исходное для проверки: подставляем , ,
Что же получается, – посторонний корень?
Думаю, интрига затянулась, настало время объяснить, почему получаются какие-то посторонние корни.
Опять объяснять буду на примере:
, но если мы возведем в квадрат обе части, , .
То же самое получается и в нашем примере с иррациональным уравнением.
В результате преобразования мы можем найти все корни, но могут примешаться и посторонние, которые и надо отфильтровать проверкой, проверив, будет ли соблюдаться равенство исходного уравнения при их подстановке.
А если взять не квадрат, а третью степень:
Какой же отсюда вывод?
Ну, вообще это в свойствах корней почитаешь («Корень степени n > 1 и его свойства»), а так я напомню только основные принципы:
- Если показатель степени четный, т.е. мы берем корень квадратный или корень степени и т.д.,
- Если подкоренное выражение отрицательно , то корень не имеет смысла (не существует);
- Если подкоренное выражение равно нулю, то корень тоже равен нулю;
- Если подкоренное выражение положительно, то значение корня существует и положительно.
Примеры:
– не существует,
А если показатель степени нечетный:
( ), то корни определены при любом значении подкоренного выражения.
корень отрицателен, если подкоренное выражение отрицательно;
равен нулю, если подкоренное выражение равно нулю;
положителен, если покоренное выражение положительно.
Примеры:
Но не все так просто как хотелось бы, и опять пример:
В этом примере есть два подкоренных выражения и число .
Чтобы избавиться от корня нужно обе части возвести в квадрат, но прежде чем это сделать перенесем в правую часть.
«Зачем?» – спросишь ты.
Дело в том, что если возводить в квадрат в таком виде то упрощать придется дольше, не веришь – попробуй сам, я, пожалуй, избавлю себя от расписывания этого.
Теперь возводим в квадрат обе части и упрощаем.
Понял в чем сложность?
Да, этот метод решения (математики называют его «метод уединения радикала».
Метод уединенного радикала
Радикал, а попросту выражение с корнем надо уединить в одной стороне уравнения) предусматривает возможность того, что уединять и возводить в степень придется не один раз.
Какие замысловатые махинации по уединению одного из выражений с корнем в одной стороне и возведении всего выражения в степень нужно делать пока от корней не избавимся вовсе, чтоб получилось нормальное такое, рациональное уравнение (без корней в смысле).
Но с другой стороны, можно заметить, что на определенной стадии решения становится без дальнейших упрощений понятно, что в уравнении, например, нет решений.
На этапе, когда мы получили вместо того, чтобы тупо возводить все очередной раз в квадрат можно прикинуть, что квадратный корень берется только из неотрицательных чисел, значит, икс в данном случае будет больше либо равен нолю.
А что из этого следует?
А то, что икс не может быть равен , т.к. и икс и корень из икс неотрицательны. В то время, как равенство говорит, будто неотрицательное умноженное на отрицательное равно неотрицательному, но все ведь знают, что минус на плюс дает минус.
Значит это равенство возможно лишь в случае, когда икс равен нолю. Я бы назвал решение методом уединения радикала решением «в лоб», а изложенный сейчас способ более рациональным с точки зрения лишней писанины и подсчетов. Е
сли ты понял то, что я сейчас объяснял, то тебе, возможно, стоит ознакомиться с этой темой в изложении для среднего уровня (см. далее).
Вернемся к нашему несчастному примеру,
Опять возводим в квадрат обе части.
Дальше, как ты уже запомнил нужно подставить корни и в исходное уравнение для проверки, скажу лишь, что тут будет побочным корнем, а ты давай, давай, подставляй, проверь на всякий случай.
А ответ, соответственно будет .
Решать тебе, применять до последнего метод уединения радикала или на определенной стадии решить, что выражение можно не упрощать больше и решение очевидно и сейчас.
Давай сделаем выжимку из сказанного выше.
Решение иррациональных уравнений включает в себя 3 шага:
- Уединить одно из выражений с корнем в одной части и избавиться от знака корня (возвести в соответствующую степень обе части уравнения и упростить его) – повторять эту процедуру пока все корни не уйдут или пока решение не станет очевидным;
- Решить получившееся рациональное уравнение;
- Для проверки подставить получившиеся корни уравнения в исходное уравнение.
Вот, собственно, и все, а чтоб слова которые ты тут прочел не остались просто словами и ты на собственном опыте понял, что здесь к чему, вот порешай:
Примеры для самостоятельной работы:
Решения примеров для самостоятельной работы:
но не проходит проверку
2. реши самостоятельно. Подсказка: Ответ :
3.
, но не проходит проверку.
Так же можно на второй строке решения понять, что равенство не имеет смысла, т.к. , только в случае, когда , но в данном случае не подходит.
СРЕДНИЙ УРОВЕНЬ
Иррациональным называется уравнение, содержащее переменную под знаком радикала (корня).
Чтобы хорошо понять, о чем здесь пойдет речь, повтори темы:
Простейшие иррациональные уравнения
Два примера:
Начнем с самого простого: уравнения вида .
Например: . Как его решить? Как избавиться от корня? Правильно, квадратный корень убирается возведением в квадрат:
А как решить такое: ?
И снова вспомним определение корня степени : – это такое число, которое нужно возвести в степень , чтобы получить . В данном случае эта степень равна :
Итак, общее правило:
Хорошо, а что с этим: ? Все просто: квадрат и корень уничтожаются, и получаем , верно?
Когда мы проходили корни, на это обращали особое внимание: здесь два корня – и , ведь .
Не забываем правило:
Реши сам:
Ответы:
Учет ОДЗ
Помнишь, что такое ОДЗ? ОДЗ (область допустимых значений) уравнения или неравенства – это множество значений переменной, при которых обе части данного уравнения (или неравенства) имеют смысл.
Например, в уравнении присутствует квадратный корень. А квадратный корень не имеет смысла, если подкоренное выражение отрицательно. То есть, в данном случае ОДЗ – это решения неравенства .
Нет необходимости искать ОДЗ в каждой задаче, содержащей корень.
Взять, например, задачу из предыдущей главы: . При возведении в квадрат получаем , то есть подкоренное выражение автоматически неотрицательно! Так зачем лишняя писанина?
Но в некоторых случаях это может быть очень полезно.
Более того, иногда можно решить пример просто найдя ОДЗ.
Пример №1:
Но при таких правая часть уравнения неположительна, а левая, как и любой приличный квадратный корень, неотрицательна.
Тогда равенство возможно только если обе части уравнения равны нулю, то есть при : .
Ответ: .
Пример №2
Решение:
Итак, уравнение имеет смысл только при одном значении переменной. Проверим его – подставим в уравнение. Что получилось? Если получилось , все верно: корень подходит.
Ответ: .
Большинство стандартных иррациональных уравнений не требуют нахождения ОДЗ – как и в приведенном в начале примере, ОДЗ оказывается автоматически учтенной после равносильного преобразования.
Иррациональные уравнения вида √A = √B
Здесь и далее большими буквами , , , и т.д. я буду обозначать не переменные или параметры, а целые выражения, содержащие переменную. Так, общая запись соответствует, например, уравнению : здесь и .
Как решить такое уравнение?
Во-первых, корни равны только когда подкоренные выражения равны: .
Но недаром мы недавно вспоминали про ОДЗ. Есть ли какие-нибудь ограничения в этом уравнении?
Действительно, чтобы уравнение имело смысл, необходимо, чтобы оба подкоренных выражения были неотрицательны:
Но поскольку эти выражения равны друг другу, достаточно потребовать неотрицательности только одного из них:
Примеры (реши сам):
Ответы:
1. Какое из выражений будем проверять на неотрицательность? Конечно же то, которое проще, то есть :
Все понятно в этих решениях? Если нет, значит ты скорее всего не повторил тему «Квадратные неравенства».
Иррациональные уравнения вида A√B = 0
Что написано в левой части? Правильно, произведение выражений. А при каких условиях произведение равно нулю? Конечно, если один из множителей равен нулю, то есть верна совокупность
Но, как ты догадался, это еще не все. Что нужно добавить? ОДЗ. Причем в той части, где , все хорошо.
Но если мы выбираем , придется кое-что сказать и про :
Примеры (реши сам):
Ответы:
Иррациональные уравнения вида √A=B
Наиболее распространённый тип иррациональных уравнений.
Возводим обе части в квадрат:
Все верно? Это ответ?
– все и правда верно, – подходящий корень.
– а вот здесь ошибка. Значит, корень – сторонний.
И правда, мы ведь помним, что результат извлечения квадратного корня всегда неотрицателен! Значит, прежде чем возводить в квадрат, нужно убедиться, что правая часть неотрицательна. Тоже своего рода ОДЗ.
Проверять же ОДЗ корня ( ) здесь снова не нужно (почему?).
Примеры:
Ответы:
Корни степени больше 2
Ты спросишь: а что всё про квадратные корни? Как же быть с остальными степенями?
Спрошу в ответ: а чем они отличаются?
Отличие, на самом деле, есть. Но важна не конкретная степень корня, а четность этой степени.
I. Корни четной степени.
Корни , , , и т.д. степеней очень похожи друг на друга, и принцип решения уравнений с ними абсолютно одинаковый. Дело в том, что корень четной степени можно всегда привести к квадратному (вспоминаем тему «Корень и его свойства»!):
II. Корни нечетной степени.
С нечетными степенями ( , , …) все намного проще!
Дело в том, что корень нечетной степени можно извлекать из любого числа! (И снова, если ты этого не знал, вспомни тему «Корень и его свойства»!)
Теперь никаких дополнительных условий, никаких ограничений – просто возводим все в нужную степень и решаем:
Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Довольно часто в уравнениях встречается знак корня и многие ошибочно считают, что такие уравнения сложные в решении. Для таких уравнений в математике существует специальный термин, которым и именуют уравнения с корнем – иррациональные уравнения.
Главным отличием в решении уравнений с корнем от других уравнений, например, квадратных, логарифмических, линейных, является то, что они не имеют стандартного алгоритма решения. Поэтому чтобы решить иррациональное уравнение необходимо проанализировать исходные данные и выбрать более подходящий вариант решения.

В большинстве случаев для решения данного рода уравнений используют метод возведения обеих частей уравнения в одну и ту же степень
Допустим, дано следующее уравнение:
Возводим обе части уравнения в квадрат:
[sqrt<(5х-16))>^2 =(x-2)^2], откуда последовательно получаем:
Получив квадратное уравнение, находим его корни:
Если выполнить подстановку данных значений в уравнение, то получим верное равенство, что говорит о правильности полученных данных.
Где можно решить уравнение с корнями онлайн решателем?
Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать – это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Наш искусственный интеллект решает сложные математические задания за секунды.
Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!
