Число компонентов связности графа

Две вершины графа называют связанными, если между ними существует путь. Любая вершина по определению связана сама с собой.

Неорграф называется связным, если любая пара вершин в нем связана. Орграф называется связным, если соответствующий ему неорграф связен. Орграф называется сильно-связным, если для любой пары несовпадающих вершин v_i и v_j существуют оба маршрута (v_i‑v_j) и (v_j‑v_i).

Бинарное отношение связности в неорграфе (сильной связности в орграфе) является отношением эквивалентности на множестве вершин, поскольку оно рефлексивно, симметрично и транзитивно. И по теореме о разбиении множества на классы эквивалентности, множество вершин графа можно разбить на такие непересекающиеся подмножества, что в каждом из этих подмножеств вершины будут попарно связаны между собой и не связаны с вершинами никаких других подмножеств. Вершинно-порожденные подграфы каждого из подмножеств в этом разбиении называются компонентами графа (сильными компонентами в орграфе). Таким образом, справедливо следующее утверждение: любой неорграф разбивается единственным образом на попарно непересекающиеся компоненты (или, как говорят, в прямую сумму своих компонент, а орграф – в прямую сумму сильных компонент).

На рисунке 26 изображены два графа: неорграф (слева) связным не является и состоит из четырех компонент – <1,2,3>, <4,5>, <6,7,8>и <9>. Орграф (справа) связен, но не сильно-связен, имеет три сильные компоненты – <1,2,3>, <4>и <5>.

Свойства связных графов

1) Связный граф состоит из одной компоненты, а число компонент в несвязном графе всегда больше единицы.

2) Изолированная вершина является компонентой.

3) В связном графе любые два пути максимальной длины имеют общую вершину.

4) Удаление циклического ребра не нарушает связности графа.

Связный граф без циклов называется деревом. Граф, каждая компонента которого является деревом, называется лесом. На рисунке 27 изображен лес, состоящий из двух деревьев.

Теорема 3.9.1. (Оценка числа ребер в простых графах)

Пусть G=(V, E) – простой граф с в вершинами и k компонентами. Тогда число его ребер р удовлетворяет неравенству:

Доказательство: 1) рассмотрим левую часть неравенства. Если граф связен, то число его компонент k равно 1. Удалим из графа все циклические ребра, в результате этого будет получено дерево. Дальнейшее удаление ребер из дерева будет нарушать связность. Поэтому среди всех связных простых графов дерево имеет наименьшее число ребер. Но число ребер в дереве равно максимальной длине пути, построенного на в вершинах, и по свойствам путей равно (в‑1). Тем самым, в связном графе число ребер р ³ в‑1, что совпадает с оценкой снизу при k=1. Пусть теперь G несвязный граф. Тогда он разбивается на k связных компонент, для каждой из которых число ребер р_i ³ в_i‑1, где i=1,2,¼,k и р_i, в_i – это число ребер и вершин в i‑ой компоненте. Но и , а 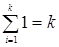. Поэтому р ³ в‑k, и левая часть неравенства доказана.

2) Теперь рассмотрим правую часть неравенства (оценку сверху). Если граф связен, то добавим к нему новые ребра, соединяя все пары несмежных вершин. В результате этого будет получен полный граф. Дальнейшее добавление ребер к полному графу будет нарушать его простоту. Поэтому среди всех связных простых графов полный граф имеет наибольшее число ребер. Для подсчета этого числа воспользуемся теоремой о степенях вершин в графе. Поскольку каждая вершина полного графа смежна со всеми остальными его вершинами, то степень каждой вершины равна (в‑1), а сумма степеней всех вершин равна в×(в‑1). По теореме о степенях вершин это число равно удвоенному числу ребер, поэтому число ребер в полном графе равно . И число ребер в связном графе р £, что совпадает с оценкой сверху при k=1. Пусть теперь G – несвязный граф. Тогда число ребер в каждой i‑ой компоненте р_i £. Однако, простое суммирование этого неравенства по числу компонент, как это было сделано в первом пункте доказательства, ничего не даст, поэтому выполним над графом следующую процедуру. Выберем произвольно две компоненты: i‑ую и j‑ую. Можно считать, что число вершин выбранных компонент в_i ³ в_j > 1. Заменим i‑ую компоненту на полный граф с числом вершин (в_i +1), а j‑ую компоненту – на полный граф с числом вершин (в_j ‑1). Общее число вершин в выбранных компонентах при этом не изменится, а число ребер изменится на величину, равную

Таким образом, выполненная процедура только увеличивает число ребер. Будем выполнять её над выбранными компонентами до тех пор, пока от j‑ой компоненты не останется одна изолированная вершина. Затем выберем другую пару компонент с числом вершин больше единицы в каждой. И выполним над этой парой такую же процедуру. И т.д. до тех пор, пока не будет получен граф, в котором с (k‑1) компонента являются изолированными вершинами и одна компонента – полный граф на (в‑k+1) вершинах. Число ребер в полученном графе равно 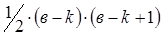, и оценка сверху доказана.

Следствие. Любой простой граф с в вершинами и числом ребер, большим, чем связен.

Не нашли то, что искали? Воспользуйтесь поиском:

Компонента сильной связности графа — Орграф называется сильно связным (strongly connected), если любые две его вершины сильно связаны. Две пары вершин s и t любого графа сильно связаны, если существует ориентированный путь из s в t и ориентированный путь из t в s. Сильно связными… … Википедия

Компонента — Компонент (от лат. componens, родительный падеж componentis составляющий) составная часть, элемент чего либо. В разных отраслях науки и техники может иметь дополнительное, более специфическое значение. В математике сложилось употребление в… … Википедия

ГРАФА СВЯЗНОСТЬ — одна из топологических характеристик графа. Граф наз. связным, если для любых его вершин и н vсуществует цепь, соединяющая эти вершины. Числом вершинной связности графа G [обозначение ] наз. наименьшее число вершин, удаление к рых (вместе с… … Математическая энциклопедия

ГРАФА АВТОМОРФИЗМ — изоморфное отображение графа на себя (см. Графов изоморфизм). Множество всех автоморфизмов данного графа образует группу относительно операции композиции автоморфизмов. Автоморфизмы графа Gпорождают группу подстановок вершин Г(G), наз. группой… … Математическая энциклопедия

Компонента сильной связности в орграфе — Орграф называется сильно связным (англ. strongly connected), если любые две его вершины сильно связаны. Две вершины s и t любого графа сильно связаны, если существует ориентированный путь из s в t и ориентированный путь из t в s.… … Википедия

Связность графа — Связный граф граф, содержащий ровно одну компоненту связности. Это означает, что между любой парой вершин этого графа существует по крайней мере один путь. Содержание 1 Примеры применения 2 Связность для орграфов … Википедия

Компонент — Компонента составная часть чего либо целого. В разных отраслях науки и техники может иметь дополнительное, более специфическое значение. В математике Компонента связности Компонента связности графа Компонента вектора или тензора, см.… … Википедия

КС — Компонента связности графа Конституционный суд Контактная сеть Counter Strike Кубок Стэнли Корреспондентский счёт (к/с) Качугин, Солодовников (по другим данным Керосиновая смесь) Координационный совет Кран Самоходный (см. также Подъёмный кран#По… … Википедия

Словарь терминов теории графов — Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице). # А Б В Г Д Е Ё Ж З И К Л М Н О П Р С … Википедия

Глоссарий теории графов — Эта страница глоссарий. См. также основную статью: Теория графов Здесь собраны определения терминов из теории графов. Курсивом выделены ссылки на термины в этом словаре (на этой странице) … Википедия

вторник, 28 августа 2012 г.

Нахождение количества компонент связности

Рассмотрим базовую задачу.
Условие:
Дан неориентированный граф G, имеющий N вершин и M ребер. Чтобы все рассмотренные подходы имели практических смысл, ограничим N

Компонента связности неориентированного графа является подграф, в котором для любой пары вершин v и u существует путь. Между двумя различными компонентами связности не существует пути.

Задача стара, как мир. Но тем не менее сегодня покажу несколько подходов по ее решению.

1. Поиск в глубину(DFS)
Самое классическое решение. Даже комментировать особо нечего.

Граф храним в виде списка смежности(строка 2). Общая сложность решения $latex O(N + M)$.
Решение

2. DSU подобная структура(ленивый подход)
Будем делать конденсацию компоненты в одну вершину. Идея следующая: будем последовательно обрабатывать ребра. Каждая компонента связности будет представлена одной своей вершиной(титульная). При этом неважно какой. По ходу обработки ребер титульная вершина компонент может меняться.
В итоге для нахождения количества компонент связности нужно найти количество титульных вершин.

1. const int SIZE = 1e3 + 10;
2. int p[SIZE];
3. bool usd[SIZE];
4. .
5. int connected_components_amount_dsu() <
6. scanf( "%d %d" , &n, &m);
7. for ( int i=1;i for ( int i=0;i "%d %d" , &f, &s);
8. int par = p[f];
9. for ( int j=1;j if (p[j] == par)
10. p[j] = p[s];
11. >
12. >
13. for ( int i=1;i true ;
14. int cnt = 0;
15. for ( int i=1;i if (usd[i]) ++cnt;
16. >
17. return cnt;
18. >

* This source code was highlighted with Source Code Highlighter .

Заметим, что сам граф непосредственно вообще никак не хранится. Общая сложность $latex O(M*N)$
Решение

3. Система непересекающихся множеств (DSU)
Реализацию, представленную выше можно существенно усовершенствовать. При добавлении нового ребра будем “мерджить меньшее подмножество к большему” + сжимать пути. У emaxx’а рассматривается доказательство того, что ассимптотика обработки одного ребра равна $latex O(alpha (N))$, где $latex alpha (N)$ – обратная функция Аккермана.

1. const int SIZE = 1e3 + 10;
2. int p[SIZE];
3. int size[SIZE];
4. int par( int x) <
5. return p[x] == x ? x : p[x] = par(p[x]);
6. >
7. int connected_components_amount_dsu() <
8. scanf( "%d %d" , &n, &m);
9. for ( int i=1;i for ( int i=0;i "%d %d" , &f, &s);
10. f = par(f); s = par(s);
11. if (f != s) <
12. if (size[f] > size[s])
13. swap(f,s);
14. p[f] = s;
15. size[s] += size[f];
16. >
17. >
18. bool usd[SIZE];
19. memset(usd, 0, sizeof (usd));
20. for ( int i=1;i true ;
21. int cnt = 0;
22. for ( int i=1;i if (usd[i]) ++cnt;
23. >
24. return cnt;
25. >

* This source code was highlighted with Source Code Highlighter .

Как и прежде сам граф не хранится в виде матрицы смежности. Общая сложность $latex O(M * alpha (N))$

4. Алгоритм Флойда.
Этот подход для самых ленивых, правда он требует хранить граф явно в виде матрицы смежности.
Запускаем алгоритм Флойда и строим матрицу достижимости для каждой пары вершин. В результате если первоначально adj[u][v] указывало на наличие ребра между u и v, то после работы алгоритма adj[u][v] будет указывать на наличие пути между u и v. После чего можно написать DFS двумя вложенными циклами.

1. const int SIZE = 1e3 + 10;
2. int adj[SIZE][SIZE];
3. bool usd[SIZE];
4. .
5. int connected_components_amount_floyd() <
6. for ( int k=1;k for ( int i=1;i for ( int j=1;j if (adj[i][k] + adj[k][j] == 2)
7. adj[i][j] = 1;
8. >
9. >
10. >
11. int cnt = 0;
12. for ( int i=1;i if (!usd[i]) <
13. ++cnt;
14. usd[i] = true ;
15. for ( int j=1;j if (adj[i][j] && !usd[j])
16. usd[j] = true ;
17. >
18. >
19. >
20. return cnt;
21. >

* This source code was highlighted with Source Code Highlighter .

Алгоритм ужасно долгий, но зато пишется довольно просто. Общая сложность $latex O(< N >^< 3 >) $
Решение

Собственно пока и все. Мы рассмотрели 3 принципиально разных подхода. На маленьких ограничениях можно выбрать тот из них, что больше по душе.