Чему равен гиперболический синус

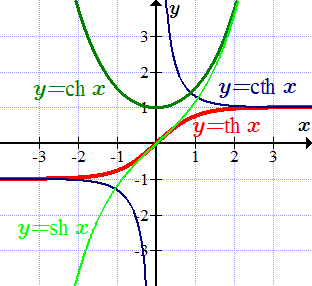
Определения гиперболических функций, их области определений и значений

Графики гиперболических функций

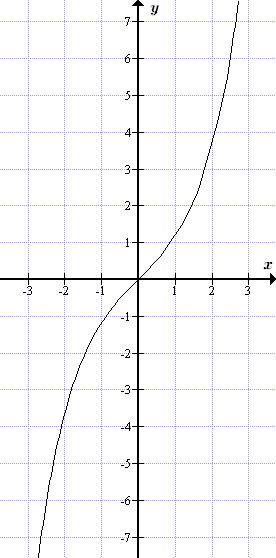
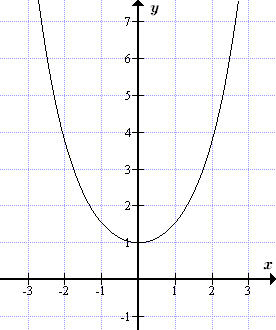
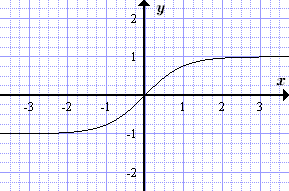
Формулы с гиперболическими функциями

Связь с тригонометрическими функциями

sin iz = i sh z ; cos iz = ch z
sh iz = i sin z ; ch iz = cos z
tg iz = i th z ; ctg iz = – i cth z
th iz = i tg z ; cth iz = – i ctg z
Здесь i – мнимая единица, i 2 = – 1 .

Применяя эти формулы к тригонометрическим функциям, получаем формулы, связывающие гиперболические функции.

Четность

sh( –x ) = – sh x ; ch( –x ) = ch x .
th( –x ) = – th x ; cth( –x ) = – cth x .

Функция ch( x ) – четная. Функции sh( x ) , th( x ) , cth( x ) – нечетные.

Разность квадратов

ch 2 x – sh 2 x = 1 .

Формулы суммы и разности аргументов

sh( x ± y ) = sh x ch y ± ch x sh y ,
ch( x ± y ) = ch x ch y ± sh x sh y ,
,
,

sh 2 x = 2 sh x ch x ,
ch 2 x = ch 2 x + sh 2 x = 2 ch 2 x – 1 = 1 + 2 sh 2 x ,
.

ОПРЕДЕЛЕНИЕ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ

Гиперболический синус
sh x = (e x – e -x )/2

Гиперболический косинус
ch x = (e x + e -x )/2

Гиперболический тангенс
th x = (e x – e -x )/(e x + e -x )

Гиперболический котангенс
cth x = (e x + e -x )/(e x – e -x )

Гиперболический секанс
sech x = 2/(e x + e -x )

Гиперболический косеканс
csch x = 2/(e x – e -x )

ОТНОШЕНИЯ МЕЖДУ ГИПЕРБОЛИЧЕСКИМИ ФУНКЦИЯМИ

cth x = 1/th x = ch x/sh x

ch 2 x – sh 2 x = 1

sech 2 x + th 2 x = 1

cth 2 x – csch 2 x = 1

ФУНКЦИИ ОТРИЦАТЕЛЬНЫХ АРГУМЕНТОВ

ФОРМУЛЫ СЛОЖЕНИЯ

ch (x ± y) = ch x ch y ± sh x sh y

th(x ± y) = (th x ± th y)/(1 ± th x.th y)

cth(x ± y) = (cth x cth y ± l)/(cth y ± cth x)

ФОРМУЛЫ ДВОЙНЫХ УГЛОВ

sh 2x = 2 sh x ch x

ch 2x = ch 2 x + sh 2 x = 2 ch 2 x – 1 = 1 + 2 sh 2 x

th 2x = (2th x)/(1 + th 2 x)

ФОРМУЛЫ ПОЛОВИННЫХ УГЛОВ

$ ext frac <2>= pm sqrt <2>>$ [+ если x > 0, – если x 0, – если x 3 x

ch 3x = 4 ch 3 x – 3 ch x

th 3x = (3 th x + th 3 x)/(1 + 3 th 2 x)

sh 4x = 8 sh 3 x ch x + 4 sh x ch x

ch 4x = 8 ch 4 x – 8 ch 2 x + 1

th 4x = (4 th x + 4 th 3 x)/(1 + 6 th 2 x + th 4 x)

СТЕПЕНИ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ

sh 3 x = ¼sh 3x – ¾sh x

ch 3 x = ¼ch 3x + ¾ch x

sh 4 x = 3/8 – ½ch 2x + 1/8ch 4x

ch 4 x = 3/8 + ½ch 2x + 1/8ch 4x

СУММА, РАЗНИЦА И УМНОЖЕНИЕ ГИПЕРБОЛИЧЕСКИХ ФУНКЦИЙ

sh x + sh y = 2 sh ½(x + y) ch ½(x – y)

sh x – sh y = 2 ch ½(x + y) sh ½(x – y)

ch x + ch y = 2 ch ½(x + y) ch ½(x – y)

ch x – ch y = 2 sh ½(x + y) sh ½(x – y)

sh x sh y = ½(ch (x + y) – ch (x – y))

ch x ch y = ½(ch (x + y) + ch (x – y))

sh x ch y = ½(sh (x + y) + sh (x – y))

ВЫРАЖЕНИЕ ГИПЕРБОЛТЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ДРУГИЕ

В следующем мы принимаем, что x > 0. Если x -1 a называется обратным гиперболическим синусом of x. Аналогично определяются и другие обратные гиперболические функции. Обратные гиперболические функции являются многозначными, но в случае обратных тригонометрических функций мы ограничимся основными значениями, при которых их можно рассматривать как однозначные.

Ниже приведен список основных значений [если не указано иное] обратных гиперболических функций, выраженных через логарифмические функции, которые принимаются в качестве вещественных.

Расчет гиперболических функций.

Решил тут разобраться с решением кубических уравнений. Это конечно отдельная тема, однако решение там выражается через гиперболические функции, точнее, обратные гиперболические функции. Статья и калькулятор Тригонометрические функции у нас есть, и даже есть статья и калькулятор Обратные тригонометрические функции, а вот про гиперболические функции ничего еще нет. Исправляем эту досадную оплошность. Калькулятор ниже, описание гиперболических функций — под ним.

Гиперболические функции

Функции sh, ch, th, sech определены и непрерывны на всей числовой оси. Функции cth, csch не определены в точке x=0.
Гиперболический синус является нечетной функцией, возрастающей на всей числовой оси и проходящей через нуль — . Гиперболический косинус является четной функцией, убывающей на промежутке от минус бесконечности до нуля, и возрастающей на промежутке от нуля до плюс бесконечности При этом — минимум этой функции.