Записать множество изображенное с помощью кругов эйлера

Круги Эйлера фигуры, условно изображающие множества

кругами Эйлера называют фигуры, условно изображающие множества и наглядно иллюстрирующие некоторые свойства операций над множествами. В литературе круги Эйлера иногда называют диаграммами Вен на (или диаграммами Эйлера — Венна). Круги Эйлера, иллюстрирующие основные операции над множествами, представлены на рис. 1.2 (множества, полученные в результате этих операций, отмечены штриховкой). АПВ 00 АЬВ Рис. 1.2 Пример 1.8. При помощи кругов Эйлера установим сначаг ла справедливость первого соотношения, выражающего свойство дистрибутивности операций объединения и пересечения множеств,

• На рис. 1.3,а вертикально заштрихован круг, изображающий множество А) а горизонтально — область, отвечающая пересечению множеств В и С. В итоге тем или иным способом заштрихована область, изображающая множество A U (БПС). На рис. 1.3,5 вертикально заштрихована область, соответствующая объединению множеств Л и Б, а горизонтально — объединению множеств Л и С, так что обоими способами заштрихована область, изображающая множество (A U В) П (A U С) и совпадающая с областью, заштрихованной каким-либо способом на рис. 1.3,а. Таким образом, круги Эйлера позволяют установить справедливость (1.10).
• Теперь рассмотрим второй закон де Моргана (1.7) Заштрихованная на рис. 1.4,а область изображает множество ЛИВ, а незаштрихованная часть прямоугольника Q (внешняя по отношению к заштрихованной) соответствует множеству ЛПВ. На рис. 1.4,5 части прямоугольника 12, заштрихованные вертикально и горизонтально, отвечают соответственно А и В. Тогда множеству Ли В отвечает область, заштрихованная хотя бы одним из указанных способов. Она совпадает с областью, не заштрихованной на рис. 1.4,а и отвечающей множеству ЛПБ, что устанавливает справедливость (1.11). Вопросы и задачи 1.1.

Запись m|n, где m,n € Z, означает, что число m нацело делит число п (то – делитель п). Описать заданные множества при условии, что х € N: 1.2. Доказать следующие соотношения и проиллюстрировать их кругами Эйлера: . 1.3. Установить, в каком отношении (X С Y, X Э У или X = Y) находятся множества X и У, если: а Использовать для иллюстрации круги Эйлера. 1.4. Пусть Aj – множество точек, образующих стороны некоторого треугольника, вписанного в заданную окружность. Описать объединение и пересечение всех таких множеств, если треугольники: а) произвольные; б) правильные; в) прямоугольные. Найти IK и flAi ieN i en для заданных семейств множеств: 1.6. Указать, какие из представленных ниже соотношений неверны, и объяснить, почему: 1.7.

Примеры решения в задачах

Методические указания и учебники	решения и формулы
задачи и методички	теория

Указать, какие из множеств равны между собой: . 1.8. Найти множества Ли В, АГВ, АВ, ВА и изобразить их на числовой прямой, если А = ( 1.0. Считая отрезок [0, 1] универсальным множеством, найти и изобразить на числовой прямой дополнения множеств: . 1.10. По приведенным ниже описаниям множеств людей подберите для каждой записи высказывания на языке множеств подходящую пословицу или поговорку. Надеемся, что это позволит лишний раз проанализировать смысл народных изречений. Например, если Z —множество людей, которые сами как следует не знают того, о чем говорят, то запись х £ Z можно отнести к пословице „Слышал звон, да не знает, где он, поскольку именно так говорят о человеке, наделенном указанным свойством (в данном случае — характеристическим свойством множества Z, см. 1.1).

Множества людей ft – универсальное множество всех людей, Л – добрые, 5е В – незаурядные, с большими способностями, С – глупые, D – умные, Е – поступающие по своему, не слушающие советов, F – связанные корыстными отношениями, G – много обещающие, Я – не выполняющие своих обещаний, J – злоупотребляющие своим служебным положением, К – слишком важничающие, задающиеся, L – вмешивающиеся не в свое дело, М – предприимчивые, ловкие, умеющие устраиваться, Р – берущиеся за несколько дел сразу, Q – плодотворно работающие, S – ошибающиеся, Т – чувствующие вину и возможность расплаты, U – не добивающиеся результатов, V – выдающие себя своим поведением, W- недальновидные, X – действующие заодно, не предающие друг друга, У – бывалые, опытные люди. Запись высказываний на языке множеств хеК; xeGnH; xCBCiQ; x£jrU; xeJ; хеМ; хеСПЕ; xCTnV; xEPDU; xGE; x € FnX; xeYnS; xeDOW. Пословицы и поговорки – Бодливой корове бог рог не дает. – Большому кораблю — большое плавание. – Вольному воля. – Ворон ворону глаз не выклюет. – Дуракам закон не писан. – За двумя зайцами погонишься, ни одного не поймаешь. –

• Знает кошка, чье мясо съела. – Знай сверчок свой шесток. – И на старуху бывает проруха. – Курице не тетка, свинье не сестра. – Кто смел, тот и съел. – На всякого мудреца довольно простоты. – Наделала синица славы, а море не зажгла. – Свет не без добрых людей. 1.11.
• Доказать справедливость соотношений (1.2). 1.12.
• Доказать справедливость второго из соотношений свойства дистрибутивности операций объединения и пересечения непосредственно и методом от противного. 1.13. Применив метод математической индукции, докаг -эать, что для любого натурального числа п справедливы неравенства п^2п

1 и (l + :r)n ^ 1 + ns, Vs>-1 (неравенство Бернулли). 1.14.

• Доказать, что среднее арифметическое п положительных действительных чисел не меньше их среднего геометрического, т.е. п 1.15. Брауну, Джонсу и Смиту решение задач по высшей математике предъявлено обвинение в соучастии в ограблении банка. Похитители скрылись на поджидавшем их автомобиле. На следствии Браун показал, что это был синий „Бьюик", Джонс — голубой „Крайслер", а Смит — „Форд Мустанг", но не синий.

Какого цвета был автомобиль и какой марки, если известно, что, желая запутать следствие, каждый из них указал правильно либо только марку машины, либо только ее цвет? 1.1в. Для полярной экспедиции из восьми претендентов А, В, С, Д J5, F, G и Я надо отобрать шесть специалистов: биолога, гидролога, синоптика, радиста, механика и врача. Обязанности биолога могут выполнять Е и G, гидролога — В и F, синоптика — F и G, радиста — С и Д механика — С и Я, врача — А и Д но каждый из них, если будет в экспедиции, сможет выполнять лишь одну обязанность. Кого и кем следует взять в экспедицию, если F не может ехать без D — без Я и без С, С не может ехать с G, а Д — с В?

Информация расположенная на данном сайте несет информационный характер и используется для учебных целей.
© Брильёнова Наталья Валерьевна

Разделы: Математика

Современный математический язык более краток и заменяет разговорный язык специальными буквенными и символьными выражениями. Понятия и обозначения языка теории множеств составляет фундамент современного математического языка. Всякий объект, входящий во множество, называют его элементом. Например, если множество – дни недели, то понедельник элемент этого множества.

Блок 1. Множества и операции над ними.

Презентация. (Слайд 2) Вопросы к слайду 2:

1. Перечислите элементы множеств:
   а) арабских цифр; (0; 1; 2; 3; 4; 5; 6; 7; 8; 9)
   б) натуральных чисел; (1; 2; 3; 4;…)
   в) целых чисел (…-2; -1; 0; 1; 2;…).
2. Как называется множество цветов, стоящих в вазе? (букет).
3. Перечислите элементы множества планет солнечной системы. (Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун).
4. Как называется множество фруктовых деревьев и кустарников растущих у дома? (сад).
5. Приведите примеры множеств, элементами которого являются геометрические фигуры.
6. Какие названия применяют для обозначения множеств животных? (млекопитающие, земноводные, хладнокровные и т.п.).
7. Перечислите элементы множества видов спорта (футбол, теннис, волейбол и т. п.).
8. Какие названия применяют для обозначения множеств кораблей? (флотилия, эскадра).

Задайте сами множество описанием.

(Слайд 3) Множества обычно обозначают большими буквами латинского алфавита: А, В, С, Д, и т. д. Некоторые числовые множества столь часто встречающиеся в различных разделах математики, что для них ввели специальные обозначения:

N – множество натуральных чисел;

Z – множество целых чисел;

Q – множество рациональных чисел;

I – множество иррациональных чисел;

R – множество действительных чисел.

(Слайд 4) Чтобы не забыть, что перечисляемые элементы объединены вместе в некоторое множество, такое перечисление производят внутри фигурных скобок .

Например, цифры десятичной системы счисления задаются множеством

Если множество состоит из чисел, то при их перечислении иногда удобнее использовать не запятую, а знак препинания “ ; ” – точку с запятой. Так как “перечислительную” запятую можно спутать с “десятичной” запятой.

Элементы множества можно перечислять в произвольном порядке. От изменения порядка перечисления элементов само множество не меняется. Например, множество гласных букв русского алфавита задается <А, Е, Ё, И, О, У, Ы, Э, Ю, Я>или <Э, Е, А, Ё, Я, О, Ы, И, У, Ю>.

Эти множества состоят из одних и тех же элементов, их называют равными, а для записи равенства двух множеств употребляют знак “ = ”.

Чтобы задать конечное множество, можно просто перечислить все его элементы.

Например, запись А = <2; 3; 5; 7; 11; 13>означает, что множество А состоит из первых шести простых чисел.

Однако задавать множество путем перечисления его элементов удобно только в том случае, когда их число невелико. Если число элементов множества достаточно велико или множество бесконечно, то явное перечисление элементов такого множества невозможно.

Способы задания, описания множеств весьма разнообразны. Например, множество всех квадратов натуральных чисел можно записать <1; 4; 9; 16; 25; …>, а множество всех чисел, которые больше 5 и меньше 12 записать <х | 5 2 – 1 2 + 16х ? – 64>?

(Слайд 8) Возьмем множество А = <2; 4; 6>и В = <1; 2; 3; 4; 5; 6; 7>. Каждый элемент множества А принадлежит также и множеству В. В таких случаях говорят, что множество А является подмножеством множества В, и пишут: А В.

Знак “” называют знаком включения.

Соотношения между множествами А и В можно проиллюстрировать на рисунке с помощью так называемых кругов Эйлера ( Леонард Эйлер российский ученый — математик, механик, физик и астроном.). Множество изображается в виде некоторого круга, а его элементы изображаются точками этого круга (рис 1).

Пустое множество считают подмножеством любого множества. А В. Будем считать, что все элементы рассматриваемых множеств взяты из некоторого одного и того же “универсального” множества К. Это множество будем изображать квадратом, а рассматриваемые множества А, В, С, … – подмножества множества К – кругами (или другими полученными из них фигурами, которые выделим штриховкой).

(Слайд 9) Задание 3. [3; 1]

Поставьте вместо … знак включения ( или ) так, чтобы получилось верное утверждение: а) А… D; б) А…В; в) С…А; г) С…В.

Верно ли, что: а) А В; б) В С; в) С А; г) С В?

(Слайд 10) Из данных множеств с помощью специальных операций можно образовывать новые множества:

1) Пересечением множества А и В называют множество, состоящие из всех общих 11элементов множеств А и В, т. е. из всех элементов, которые принадлежат и множеству А, и множеству В (рис. 2). Пересечение множеств А и В обозначают так: АВ. Это определение можно записать и так: АВ = <х | х А и х В>. Иными словами, пересечение двух множеств – это их общая часть. Например, если А = <3; 9; 12>и В = <1; 3; 5; 7; 9; 11>, то АВ = <3; 9>. Если А = <10; 20; …90; 100>и В = <6; 12; 18;…>, то АВ = <30; 60; 90>. Можно рассматривать пересечение не только двух, но трех, четырех и т. д. множеств. Пересечение множеств В, С и D обозначают так: ВСD.

(Слайд 11) Задание 4. [3; 1]

Найдите: а) АВ; б) АС; в) СВ.

2. Даны множества: А – множества всех натуральных чисел, кратных 10, В = <1; 2; 3;…, 41>.

Найдите АВ.

Найдите (АВ) С.

2) Объединением множеств А и В называют множество, состоящее из всех элементов, которые принадлежат хотя бы одному из этих множеств – или множеству А, или множеству В (рис. 3). Объединение множеств А и В обозначают так: АUВ.

Это определение можно записать и так: АUВ = <х | х А или х В>. Например, если А = <3; 9; 12>и В = <1; 3; 5; 7; 9; 11>, то АUВ = <1; 3; 5; 7; 9; 11; 12>. Можно рассматривать объединение не только двух, но трех, четырех и т.д. множеств. Объединение множеств В, С и D обозначают так: ВUСUD.

(Слайд 13) Задание 5. [3; 1]

Найдите: а) АUВ; б) АUС; в) СUВ.

3. Даны три числовых промежутка: А = (7,7; 11), В = [; ], С = (; 13].

Круги Эйлера, на самом деле, достаточно часто встречаются в нашей жизни. Еще в младшей школе ученики начинают работать со схематическими фигурами, которые наглядно объясняют соотношения предметов и понятий.

Описание схемы кругов Эйлера

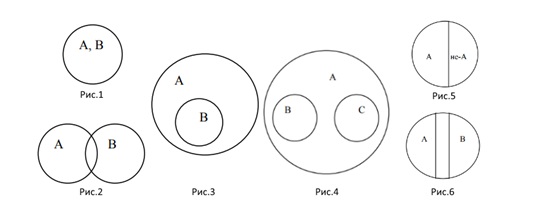
Круги Эйлера – геометрические конструкции, применяемые для упрощения восприятия логических связей между предметами, понятиями и явлениями.

Делятся на группы, в зависимости от типа отношений между множествами:

• равнозначные (рис.1);
• пересекающиеся (рис.2);
• подчиненные (рис.3);
• соподчиненные (рис.4);
• противоречащие (рис.5);
• противоположные (рис.6).

Типовой пример такой диаграммы:

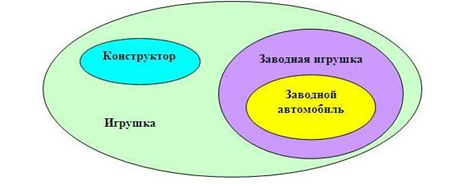
Наибольшее множество, отмеченное зеленым цветом, представляет собой все варианты игрушек.

Одним из вариантов игрушек являются конструкторы. Они выделены голубым овалом. Конструкторы являются отдельным множеством, и, одновременно, частью множества «Игрушки».

Заводные игрушки также являются частью множества «Игрушки», но не относятся к множеству «Конструкторы». Поэтому, они выделяются фиолетовым овалом. А вот множество «Заводных автомобилей» является самостоятельным, но при этом, является подмножеством «Заводных игрушек».

При помощи этого метода ученый решал сложнейшие математические задачи. Применение простых фигур позволяло свести решение любой, даже самой сложной задачи, к символической логике – максимальному упрощению рассуждений.

Позже, данный способ был доработан англичанином Джоном Венном, который ввел понятие пересечения нескольких множеств.

Методика очень проста в использовании — круги Эйлера для дошкольников от 4-5 лет начинают преподавать уже в детском саду. При этом, она же на столько удобна, что применяется даже в высшей академической среде.

Применение кругов Эйлера

Основная цель использования диаграмм – практическое решение задач по объединению или пересечению множеств.

Области применения: математика, логика, менеджмент, статистика, информатика и др. На самом деле, их значительно больше, но перечислить все попросту невозможно.

Диаграммы делятся на два вида.

Первый описывает объединение понятий, вложенность одного в другое. Пример приведен в статье выше.

Второй описывает пересечения двух разных множеств некоторыми общими признаками. Один из примеров

Примеры задач и решения

Рассмотрим задачи, в которых помогают разбираться круги Эйлера, примеры решения задач по логике и математике.

Задачи для дошкольников

Первые в очереди: круги Эйлера для дошкольников, задания с ответами на которые помогут понять, как малыши впервые знакомятся с методикой упрощения сложных математических и логических задач.

Задание №1 – начальный уровень.

Цель: научить ребенка определять предмет, наиболее соответствующий одновременно двум свойствам.

Правильный ответ: кубик Рубика.

Задание №2

Правильный ответ: лягушка.

Задание №3

Правильный ответ: груша.

Задание №4 – средний уровень.

Задания усложняются тем, что используется больше множеств.

Правильный ответ: Солнце.

Задание №5

Правильный ответ: платье.

Задание №6

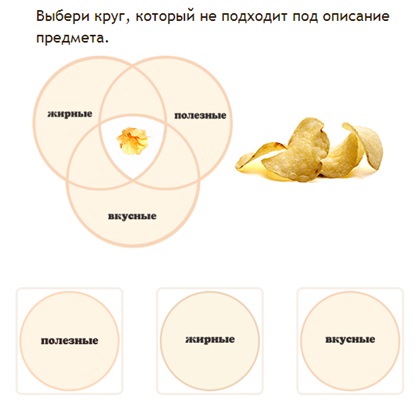
Правильный ответ: полезные.

Задания для школьников

Следующие задачи по логике с ответами, круги Эйлера в которых являются основой для решения, касаются младших школьников. Подобные задания обучают детей разбирать логические пересечения по определенным признакам.

Задание №1

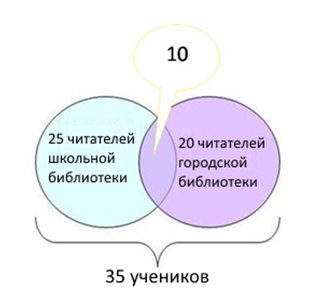
35 учеников зарегистрированы в школьной или городской библиотеках. Из них 25 регулярно посещают школьную библиотеку, а 20 – городскую.

• Посещают обе библиотеки?
• Не посещают городскую библиотеку?
• Не посещают школьную библиотеку?
• Ходят только в городскую библиотеку?
• Ходят только в школьную библиотеку?

Ответ:

• Определим количество посетителей двух библиотек – общая часть на диаграмме:

• Ученики, не посещающие городскую библиотеку:

35 – 20 = 15 – левая сектор голубой зоны.

• Ученики, не посещающие школьную библиотеку:

35 – 25 = 10 – правый сектор фиолетовой.

• Посетители только городской библиотеки:

35 – 25 = 10 – также, правый сектор фиолетовой.

• Посетители только школьной библиотеки:

35 – 20 = 15 – также, левый сектор голубой.

Задание №2 – также предназначено для младших классов, но является более сложным.

В 7-А учится 38 человек. Ученики увлекаются разными спортивными играми: 16 – баскетболом, 17 – хоккеем, 18 – футболом. Одновременно баскетбол и хоккей любят 4 человека, баскетбол и футбол – 3, хоккей и футбол – 5, а 3 ученика не интересуются спортом.

1. Есть ли ученики, увлекающиеся всеми спортивными играми?
2. Какое количество школьников интересуется только одной из спортивных игр?

Ответ:

Все ученики класса – наибольшая окружность.

Круг «Б» — баскетболисты, «Х» — хоккеисты, «Ф» — футболисты, «Z» — универсальные спортсмены. Трое неспортивных учеников просто находятся в общем круге.

Баскетболисты, входящие в множество «Б», но не входящие в зоны пересечения со множествами «Х» и «Ф».

16 – (4 + Z + 3) = 9 – Z.

По аналогии, находим количество хоккеистов.

17 – (4 + Z + 5) = 8 – Z.

18 – (3 + Z + 5) = 10 – Z.

Чтобы пределить значение Z, нужно суммировать множества учеников.

3 + (9 – Z) + (8 – Z) + (10 – Z) + 3 + 4 + 5 + Z = 38;

Соответственно, Б = 7, Ф = 8, Х = 6.

Применение круговых диаграмм позволяет наглядно продемонстрировать все взаимоотношения разных групп учеников.

Метод схематического изображения взаимоотношений множеств – не просто увлекательная вещь. Круги Эйлера, примеры решения задач, логика которых неочевидна, показывают, что метод может использоваться не только при развязывании математических заданий, но и находить выход из житейских ситуаций.