Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
Задачи по теме: «Момент инерции. Закон сохранения момента инерции и момента импульса».
На барабан радиусом R=0,5 м и с горизонтальной осью вращения намотан шнур, к концу которого привязан груз массой m = 10 кг. Найдите момент инерции барабана, если известно, что его угловое ускорение равно  . Тернием пренебречь.
. Тернием пренебречь.
m = 10 кг 

Вращение барабана происходит под
действием силы F. Из второго закона Ньютона

 = ∆ω/∆t = ∆υ/R∆t = a/R → a = εR
= ∆ω/∆t = ∆υ/R∆t = a/R → a = εR
M = Jε – момент силы через момент инерции для вращающегося тела.
M = Fd = FR – момент силы вращающей барабан.
По закону сохранения момента сил
J = (m ( g – εR) R)/ ε = 22,5 (кг м²)
Ответ: 22, 5 кг м 2
К ободу однородного диска радиусом R=0,2м массой m=1,2 кг приложена постоянная сила 100 Н, при вращении на диск действует момент силы трения, равный 5 нм. Чему равно угловое ускорение диска?
R = 0, 2 м Из оснавного управления динамики вращательного
m = 1, 2 кг движения M=Jε
F = 100 Н Сила действующая на обод F`= F – Fтр. Из M = 5 нм момента силы трения Fтр = MR = 25 Н
ε = ? Момент силы F`- M=F`R по закону сохранения
J = mR² –момент инерции обруча

Ответ: ε = 312, 5 с -2 .
Шарик, диаметр которого равен 6 см, катится по полу и останавливается через t = 2с, пройдя расстояние S = 70 см. Определите коэффициент трения качения, считая его постоянным.
d = 0, 06 м М=εJ – основное уравнение вращательного движения.
t = 2c J= 0,4mr 2 – момент инерции шара.
S= 0,7м. 
M= 0,4 m r 2 a/ r= 0,4 a m r
Момент силы трения M = F тр r
По закону сохранения момента сил
S= at 2 /2  a=2S/t 2 = 1,4/4 = 0,35 м/с 2
a=2S/t 2 = 1,4/4 = 0,35 м/с 2

Во сколько раз уменьшится угловая скорость вращения человека, если момент инерции изменится от 1 кг м² до 1,25 кг м²?
 L 1 = J 1 ω 1 – момент импульса в первом состоянии.
L 1 = J 1 ω 1 – момент импульса в первом состоянии.
 L 2 = J 2 ω 2 – момент импульса во втором состоянии.
L 2 = J 2 ω 2 – момент импульса во втором состоянии.
 L 1 = L 2 – закон сохранения момента импульса.
L 1 = L 2 – закон сохранения момента импульса.

Ответ: 
Найти момент импульса Земного шара М 3 = 6·10 24 кг, R 3 = 6,4·10³ км, если точки поверхности Земли вращаются со скоростью 36 км/ ч.
M 3 = 6·10 24 кг L = Jω J= 0,4 M 3 R 3 ²- момент инерции шара.
R 3 = 6,4·10 6 м ω = υ/ R
υ = 10 мс L = 0,4 M 3 υ R 3 = 15,36·10³º кг м²/с.
Ответ: L = 15, 36·10³º кг м²/с
Комета Галлея движется вокруг солнца по вытянутому эллипсу. Наибольшее удаление от солнца равно 35,2 а. е., а наименьшее удаление – 0,6 а.е.. Найти отношение максимальной скорости кометы к минимальной.
R 1 = 35, 2 а. е.  момент импульса при наибольшем
момент импульса при наибольшем
R 2 = 0, 6 а. е. удалении.

 момент инерции кометы при наибольшем
момент инерции кометы при наибольшем

 момент импульса кометы при
момент импульса кометы при
L 1 = L 2 – закон сохранения момента импульса.

Ответ: 
Человек стоит на вращающейся с некоторой угловой скоростью платформе. В вытянутых в сторону руках он держит по гире, массой каждой из них m = 5 кг. Расстояние от гирь до оси вращения R 1 =0,71м. Во сколько раз изменится частота вращения человека, если он прижмет к себе руки так, что расстояние от оси вращения до гири станет R 2 = 0,2 м. Момент инерции человека считайте в обоих случаях равным J 0 = 1 кг м.²
m = 5 кг Момент импульса в первом случае
R 1 =0,71м 
R 2 = 0,2 м  момент инерции в первом случае.
момент инерции в первом случае.
J 0 = 1 кг м² 

 момент инерции во втором случае.
момент инерции во втором случае.

 закон сохранения момента импульса.
закон сохранения момента импульса.

Ответ: 
Человек массой m 1 = 60 кг находится на неподвижной круглой платформе радиусом R 2 = 10м и массой m 2 = 120 кг, которая может вращаться вокруг своей вертикальной оси. С какой угловой скоростью будет вращаться платформа, если человек станет двигаться по окружности радиусом R 1 = 5м с линейной скоростью υ 1 = 2 м/с относительно платформы.
m 1 = 60 кг  момент импульса человека;
момент импульса человека;
R 2 = 10м  момент инерции человека.
момент инерции человека.
m 2 = 120 кг 
R 1 = 5м 
υ 1 = 2 м/с  момент импульса платформы
момент импульса платформы

 закон сохранения импульса.
закон сохранения импульса.

Считая Солнце однородным шаром, оцените минимальный радиус и период вращения вокруг своей оси пульсара, который мог бы образоваться после сжатия Солнца под действием силы тяготения при исчерпании внутренних источников энергии, поддерживающих высокую температуру газа. Радиус Солнца R c = 7·10 8 м, период вращения вокруг оси Т с = 2,2·10 6 с. Масса Солнца М с = 2·10³º кг.
R c = 7·10 8 м Момент импульса Солнца
Т с = 2,2·10 6 с 
М с = 2·10³º кг  момент инерции Солнца
момент инерции Солнца
R п = ? Т п = ? 
Момент импульса образовавшегося пульсара

По закону сохранения импульса

Вращение пульсара происходит под действием силы тяготения.

Для удобства расчета (*) возведем в квадрат

Ответ: R п =
Когда приходится решать задачи по физике на движение объектов, то часто оказывается полезным применение закона сохранения импульса. Что такое импульс для линейного и кругового перемещения тела, а также в чем состоит суть закона сохранения этой величины, рассматривается в статье.
Понятие о линейном импульсе
Исторические данные свидетельствуют, что впервые эту величину рассмотрел в своих научных трудах Галилео Галилей в начале XVII века. Впоследствии Исаак Ньютон смог гармонично встроить понятие о количестве движения (более правильное название импульса) в классическую теорию перемещения объектов в пространстве.
 Вам будет интересно: Что такое консументы 1 порядка? Примеры консументов
Вам будет интересно: Что такое консументы 1 порядка? Примеры консументов

Обозначим количество движения как p¯, тогда формула для его вычисления запишется в виде:
Здесь m – масса, v¯ – это скорость (векторная величина) движения. Это равенство показывает, что количество движения – это скоростная характеристика объекта, где масса играет роль коэффициента умножения. Количество движения является векторной величиной, направленной в том же направлении, что и скорость.
Интуитивно понятно, что чем больше скорость движения и масса тела, тем труднее его остановить, то есть тем большей кинетической энергией оно обладает.
Количество движения и его изменение
 Вам будет интересно: Эквивалентная доза. Радиоактивное излучение
Вам будет интересно: Эквивалентная доза. Радиоактивное излучение
Можно догадаться, что для изменения величины p¯ тела необходимо приложить некоторую силу. Пусть сила F¯ действует в течение промежутка времени Δt, тогда закон Ньютона позволяет записать равенство:
F¯ * Δt = m * a¯ * Δt; следовательно, F¯ * Δt = m * Δv¯ = Δp¯.
Величина, равная произведению промежутка времени Δt на силу F¯, называется импульсом этой силы. Поскольку она оказывается равной изменению количества движения, то последнее часто называют просто импульсом, предполагая тем самым, что некоторая внешняя сила F¯ его создала.
Таким образом, причиной изменения количества движения является импульс внешней силы. Величина Δp¯ может приводить как к увеличению значения p¯, если угол между F¯ и p¯ является острым, так и к уменьшению модуля p¯, если этот угол тупой. Наиболее простыми случаями являются разгон тела (угол между F¯ и p¯ равен нулю) и его торможение (угол между векторами F¯ и p¯ составляет 180o).
Когда сохраняется количество движения: закон
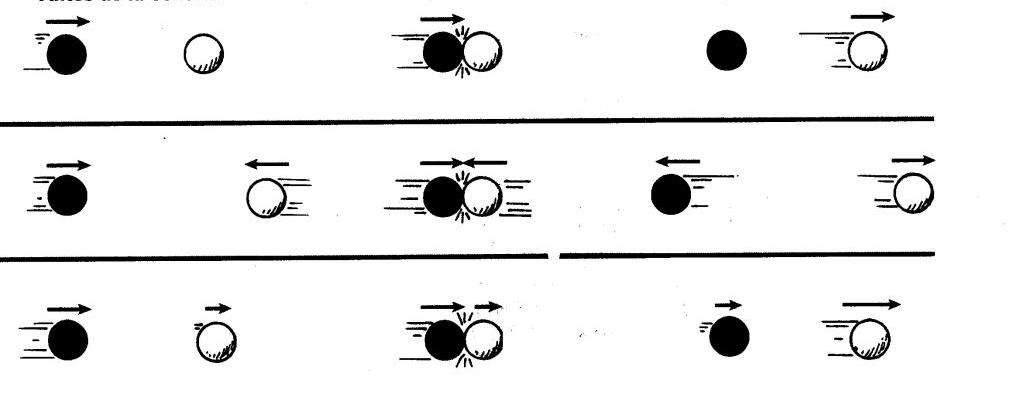
Если на систему тел не действуют внешние силы, и все процессы в ней ограничиваются только механическим взаимодействием ее составляющих, то каждая компонента количества движения остается неизменной сколь угодно длительное время. Это и есть закон сохранения импульса тел, который математически записывается так:
p¯ = ∑ipi¯= const или
∑ipix= const; ∑ipiy= const; ∑ipiz= const.
Нижний индекс i – это целое число, которое нумерует объект системы, а индексы x, y, z описывают компоненты импульса на каждую из осей координат в декартовой прямоугольной системе.
На практике часто приходится решать одномерные задачи на столкновение тел, когда известны начальные условия, и необходимо определить состояние системы после удара. В этом случае импульс сохраняется всегда, чего нельзя сказать о кинетической энергии. Последняя до и после удара будет неизменной только в единственном случае: когда имеет место абсолютно упругое взаимодействие. Для этого случая столкновения двух тел, которые движутся со скоростями v1 и v2, формула закона сохранения импульса примет вид:
m1 * v1 + m2 * v2 = m1 * u1 + m2 * u2.
Здесь скорости u1 и u2 характеризуют движение тел после удара. Отметим, что в этом виде закона сохранения необходимо учитывать знак скоростей: если они направлены друг навстречу другу, то одну следует принять положительной, а другую – отрицательной.
Для абсолютно неупругого соударения (два тела слипаются после удара) закон сохранения количества движения имеет форму:
m1 * v1 + m2 * v2 = (m1 + m2) * u.
Решение задачи на закон сохранения величины p¯
Решим следующую задачу: два шара катятся друг навстречу другу. Массы шаров одинаковые, а их скорости равны 5 м/с и 3 м/с. Полагая, что имеет место абсолютно упругое столкновение, необходимо найти скорости шаров после него.
Пользуясь законом сохранения импульса для одномерного случая, а также учитывая, что кинетическая энергия сохраняется после удара, запишем:
v12 + v22 = u12 + u22.
Здесь мы сразу сократили массы шаров ввиду их равенства, а также учли тот факт, что тела движутся друг навстречу другу.
Продолжить решение системы проще, если подставить известные данные. Получаем:
52 + 32 = u12 + u22.
Подставляя u1 во второе равенство, получаем:
34 = (2 – u2)2+u22=4 – 4u2 + 2u22; следовательно, u22 – 2u2 – 15 = 0.
Мы получили классическое квадратное уравнение. Решаем его через дискриминант, получаем:
u2 = (2 ± 8) / 2 = (5; -3) м/c.
Мы получили два решения. Если их подставить в первое выражение и определить u1, тогда получим такие значение: u1= -3 м/с, u2 = 5 м/с; u1= 5 м/с, u2 = -3 м/с. Вторая пара чисел дана в условии задачи, поэтому реальному распределению скоростей после удара она не соответствует.
Таким образом, остается лишь одно решение: u1= -3 м/с, u2 = 5 м/с. Этот любопытный результат означает, что при центральном упругом столкновении два шара равной массы просто обмениваются своими скоростями.
Момент импульса
Все, что говорилось выше, относится к линейному типу движения. Однако, оказывается, аналогичные величины можно ввести и при круговом перемещении тел вокруг некоторой оси. Момент импульса, который также называют угловым моментом, вычисляется как произведение вектора, соединяющего материальную точку с осью вращения, на импульс этой точки. То есть имеет место формула:
L¯ = r¯ * p¯, где p¯ = m * v¯.
Момент импульса, как и величина p¯, это вектор, который направлен перпендикулярно плоскости, построенной на векторах r¯ и p¯.
Величина L¯ является важной характеристикой вращающейся системы, поскольку она определяет энергию, которая в ней запасена.
Момент импульса и закон сохранения
Момент импульса сохраняется, если на систему не действуют внешние силы (обычно говорят об отсутствии момента сил). Выражение в предыдущем пункте путем несложных преобразований можно записать в более удобной для практики форме:
L¯ = I * ω¯, где I = m * r2 – момент инерции материальной точки, ω¯ – угловая скорость.
Момент инерции I, который появился в выражении, имеет абсолютно такой же смыл для вращения, что обычная масса для линейного движения.
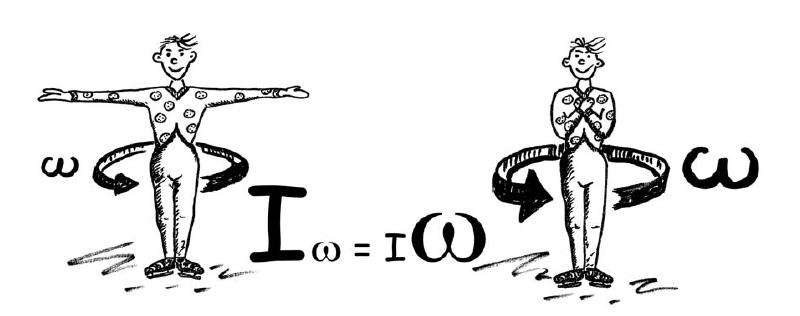
Если имеет место какая-либо внутренняя перестройка системы, при которой I изменяется, то ω¯ тоже не остается постоянной. Причем изменение обеих физических величин происходит таким образом, что равенство ниже остается справедливым:
Это и есть закон сохранения углового момента L¯. Его проявление наблюдал каждый человек, который хотя бы один раз посещал балет или фигурное катание, где спортсменки выполняют пируэты с вращением.
Задача № 1. Определите массу автомобиля, имеющего импульс 2,5•10 4 кг•м/с и движущегося со скоростью 90 км/ч.
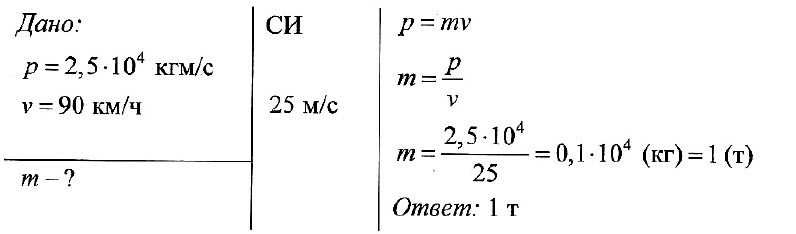
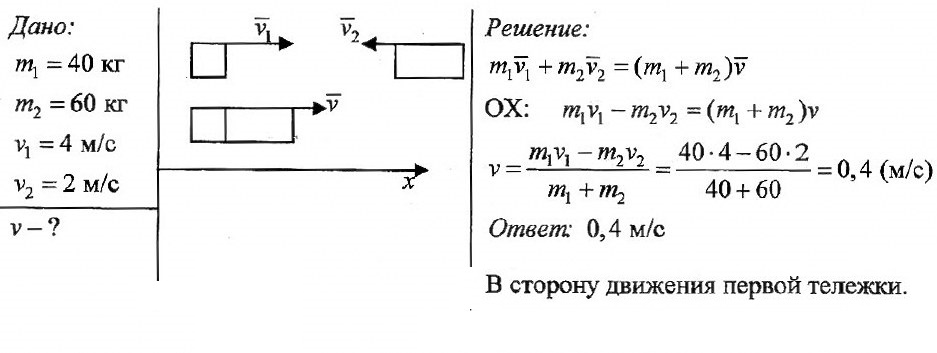
Задача № 2. Тележка массой 40 кг движется со скоростью 4 м/с навстречу тележке массой 60 кг, движущейся со скоростью 2 м/с. После неупругого соударения тележки движутся вместе. В каком направлении и с какой скоростью будут двигаться тележки ?
Задача № 3. Снаряд, выпущенный вертикально вверх, разорвался в верхней точке траектории. Первый осколок массой 1 кг приобрел скорость 400 м/с, направленную горизонтально. Второй осколок массой 1,5 кг полетел вверх со скоростью 200 м/с. Какова скорость третьего осколка, если его масса равна 2 кг?
Решение. Взрывающийся снаряд можно считать замкнутой системой, потому, что сила тяжести намного меньше, чем сила давления пороховых газов, разрывающих снаряд на осколки. Значит, можно использовать закон сохранения импульса. Поскольку разрыв снаряда произошел в верхней точке траектории, векторная сумма импульсов всех осколков должна быть равна нулю. Следовательно, векторы импульсов осколков образуют треугольник; этот треугольник прямоугольный, а искомый вектор — его гипотенуза.

Ответ: 250 м/с.
Задача № 4. К стене прикреплен шланг с насадкой, изогнутой под прямым углом (см. рисунок). Из шланга вытекает вода со скоростью v = 10 м/с. Найдите горизонтальную составляющую силы, с которой шланг давит на стену. Площадь сечения шланга S = 10 см 2 .

Ответ: 100 Н.
Задача № 5. Какую силу тяги развивает реактивный двигатель, выбрасывающий каждую секунду 10 кг продуктов сгорания топлива со скоростью 3 км/с относительно ракеты?

Ответ: 30 кН.
Задача № 6. Повышенной сложности Конькобежец массой М = 70 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой m = 3 кг со скоростью v = 8 м/с относительно льда. Найдите, на какое расстояние S откатится при этом конькобежец, если μ = 0,02.

Ответ: 0,3 м.
Задача № 7. Повышенной сложности Деревянный брусок, движущейся вертикально, падает со скоростью v = 3 м/с на горизонтальную ленту транспортера, движущегося со скоростью u = 1 м/с. Брусок после удара не подскакивает. При каком коэффициенте трения брусок не будет проскальзывать по транспортеру?
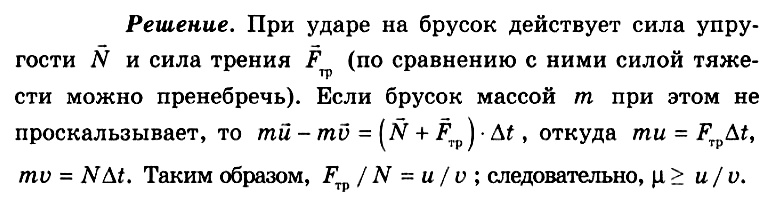
Ответ: μ ≥ 0.33
Задача № 8. ОГЭ Конькобежец массой M = 70 кг, стоя на льду, бросает в горизонтальном направлении шайбу массой m = 0,3 кг со скоростью v = 40 м/с. На какое расстояние s откатится конькобежец, если коэффициент трения коньков о лёд μ = 0,02?

Задача № 9. ЕГЭ Вагон массой m = 4•10 4 кг, движущийся со скоростью v = 2 м/с, в конце запасного пути ударяется о пружинный амортизатор. На сколько он сожмёт пружину амортизатора, жёсткость которой k = 2,25•10 6 Н/м?

Краткая теория для решения задачи на Закон сохранения импульса.

Алгоритм решения задач на закон сохранения импульса:
1. Записать «дано».
2. Сделать чертеж, на котором изобразить направления импульсов (или скоростей) каждого тела до взаимодействия и после взаимодействия.
3. Записать закон сохранения импульса для данной системы в векторной форме.
4. Выбрать координатную ось (оси), найти проекции векторов на эту ось (оси).
5. Записать закон сохранения импульса в скалярной форме.
6. Решить получившееся уравнение относительно неизвестной величины.
7. Оценить ответ на реальность.
Рассмотрим взаимодействия тел, при котором они движутся вдоль одной прямой в одном направлении или навстречу друг другу. При столкновении тела испытывают соударение. Соударение может быть двух типов: упругий удар и неупругий удар.
Упругий удар — тела после взаимодействия приобретают скорости, направленные в разные стороны.
Неупругий удар — тела после взаимодействия будут двигаться вместе, как одно целое.
Это конспект по теме «ЗАДАЧИ на Закон сохранения импульса». Выберите дальнейшие действия:
