Задачи коммивояжера решаются посредством различных методов, выведенных в результате теоретических исследований. Все эффективные методы (сокращающие полный перебор) — методы эвристические. В большинстве эвристических методов находится не самый эффективный маршрут, а приближённое решение. Зачастую востребованы алгоритмы постепенно улучшающие некоторое текущее приближенное решение. Выделяют следующие группы методов решения задач коммивояжера, которые относят к простейшим:
Полный перебор (или метод «грубой силы») — метод решения задачи путем перебора всех возможных вариантов. Сложность полного перебора зависит от количества всех возможных решений задачи. Если пространство решений очень велико, то полный перебор может не дать результатов в течение нескольких лет или даже столетий.
Обычно выбор решения можно представить последовательностью выборов. Если делать эти выборы с помощью какого-либо случайного механизма, то решение находится очень быстро, так что можно находить решение многократно и запоминать «рекорд», т. е. наилучшее из встретившихся решений. Этот наивный подход существенно улучшается, когда удается учесть в случайном механизме перспективность тех или иных выборов, т. е. комбинировать случайный поиск с эвристическим методом и методом локального поиска. Такие методы применяются, например, при составлении расписаний для Аэрофлота.
· Жадные алгоритмы (метод ближайшего соседа, метод включения ближайшего города, метод самого дешевого включения);
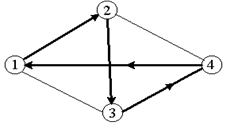
Жадный алгоритм – алгоритм нахождения наикратчайшего расстояния путём выбора самого короткого, ещё не выбранного ребра, при условии, что оно не образует цикла с уже выбранными рёбрами. «Жадным» этот алгоритм назван потому, что на последних шагах приходится жестоко расплачиваться за жадность. При решении задачи коммивояжера жадный алгоритм превратится в стратегию «иди в ближайший (в который еще не входил) город». Жадный алгоритм, очевидно, бессилен в этой задаче. Рассмотрим для примера сеть (рис. 2), представляющую узкий ромб. Коммивояжер стартует из города 1. Алгоритм «иди в ближайший город» выведет его в город 2, затем 3, затем 4; на последнем шаге придется платить за жадность, возвращаясь по длинной диагонали ромба. В результате получится не кратчайший, а длиннейший тур.
· Метод минимального остовного дерева (деревянный алгоритм);
В основе алгоритма лежит утверждение: «Если справедливо неравенство треугольника, то для каждой цепи верно, что расстояние от начала до конца цепи меньше (или равно) суммарной длины всех ребер цепи». Это обобщение расхожего убеждения, что прямая короче кривой. Деревянный алгоритм для решения задачи коммивояжера будет следующим: строится на входной сети задачи коммивояжера кратчайшее остовное дерево и удваиваются все его ребра. В результате получаем граф — связный с вершинами, имеющими только четные степени. Затем строится эйлеров цикл, начиная с вершины 1, цикл задается перечнем вершин. Просматривается перечень вершин, начиная с 1, и зачеркивается каждая вершина, которая повторяет уже встреченную в последовательности. Останется тур, который и является результатом алгоритма.
Доказано, что деревянный алгоритм ошибается менее чем в два раза, поэтому такие алгоритмы называют приблизительными, а не просто эвристическими.
· Метод имитации отжига.
Экзотическое название данного алгоритма связано с методами имитационного моделирования в статистической физике, основанными на технике Монте-Карло. Исследование кристаллической решетки и поведения атомов при медленном остывании тела привело к появлению на свет вероятностных алгоритмов, которые оказались чрезвычайно эффективными в комбинаторной оптимизации. Впервые это было замечено в 1983 году. Сегодня этот алгоритм является популярным как среди практиков благодаря своей простоте, гибкости и эффективности, так и среди теоретиков, поскольку для данного алгоритма удается аналитически исследовать его свойства и доказать асимптотическую сходимость. Алгоритм имитации отжига относится к классу пороговых алгоритмов локального поиска. На каждом шаге этого алгоритма для текущего решения ik в его окрестности N(ik) выбирается некоторое решение j и, если разность по целевой функции между новым и текущим решением не превосходит заданного порога tk, то новое решение j заменяет текущее. В противном случае выбирается новое соседнее решение. На практике применяются различные модификации более эффективных методов:
· Метод ветвей и границ;
Метод ветвей и границ предложен в 1963 году группой авторов Дж. Литлом, К. Мурти, Д. Суини, К. Кэролом. Широко используемый вариант поиска с возвращением, фактически является лишь специальным частным случаем метода поиска с ограничениями 4 . Ограничения в данном случае основываются на предположении, что на множестве возможных и частичных решений задана некоторая функция цены и что нужно найти оптимальное решение, т.е. решение с наименьшей ценой. Для применения метода ветвей и границ функция цены должна обладать тем свойством, что цена любого частичного решения не превышает цены любого расширения этого частичного решения (Заметим, что в большинстве случаев функция цены неотрицательна и даже удовлетворяет более сильному требованию). Столь большой успех применения данного метода объясняется тем, что авторы первыми обратили внимание на широту возможностей метода, отметили важность использования специфики задачи и сами воспользовались спецификой задачи коммивояжера.
В основе метода ветвей и границ лежит идея последовательного разбиения множества допустимых решений на подмножества. На каждом шаге метода элементы разбиения подвергаются проверке для выяснения, содержит данное подмножество оптимальное решение или нет. Проверка осуществляется посредством вычисления оценки снизу для целевой функции на данном подмножестве. Если оценка снизу не меньше рекорда — наилучшего из найденных решений, то подмножество может быть отброшено. Проверяемое подмножество может быть отброшено еще и в том случае, когда в нем удается найти наилучшее решение. Если значение целевой функции на найденном решении меньше рекорда, то происходит смена рекорда. По окончанию работы алгоритма рекорд является результатом его работы. Если удается отбросить все элементы разбиения, то рекорд — оптимальное решение задачи. В противном случае, из неотброшенных подмножеств выбирается наиболее перспективное (например, с наименьшим значением нижней оценки), и оно подвергается разбиению. Новые подмножества вновь подвергаются проверке и т.д.
· Метод генетических алгоритмов;
«Отцом-основателем» генетических алгоритмов считается Джон Холланд, книга которого «Адаптация в естественных и искусственных системах» (1975) является основополагающим трудом в этой области исследований. Генетический алгоритм — это эвристический алгоритм поиска, используемый для решения задач оптимизации и моделирования путём случайного подбора, комбинирования и вариации искомых параметров с использованием механизмов, напоминающих биологическую эволюцию. Является разновидностью эволюционных вычислений. Отличительной особенностью генетического алгоритма является акцент на использование оператора «скрещивания», который производит операцию рекомбинации решений-кандидатов, роль которой аналогична роли скрещивания в живой природе. Генетические алгоритмы служат, главным образом, для поиска решений в многомерных пространствах поиска.
· алгоритм муравьиной колонии.
Алгоритмы муравья, или оптимизация по принципу муравьиной колонии (название было придумано изобретателем алгоритма, Марко Дориго), основаны на применении нескольких агентов и обладают специфическими свойствами, присущими муравьям, и используют их для ориентации в физическом пространстве. Алгоритмы муравья особенно интересны потому, что их можно использовать для решения не только статичных, но и динамических проблем, например, в изменяющихся сетях.
2.4 Метод ветвей и границ
Для решения задачи коммивояжера методом ветвей и границ необходимо выполнить следующую последовательность действий:
(1) Построение матрицы с исходными данными.
(2) Нахождение минимума по строкам.
(3) Редукция строк.
(4) Нахождение минимума по столбцам.
(5) Редукция столбцов.
(6) Вычисление оценок нулевых клеток.
(7) Редукция матрицы.
(8) Если полный путь еще не найден, переходим к пункту 2, если найден к пункту 9.
(9) Вычисление итоговой длины пути и построение маршрута.
Подробная методика решения
В целях лучшего понимания задачи будем оперировать не понятиями графа, его вершин и т.д., а понятиями простыми и максимально приближенными к реальности: вершины графа будут называться «города», ребра их соединяющие – «дороги».
Итак, методика решения задачи коммивояжера:
1. Построение матрицы с исходными данными
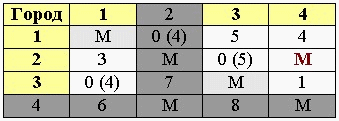
Сначала необходимо длины дорог соединяющих города представить в виде следующей таблицы:
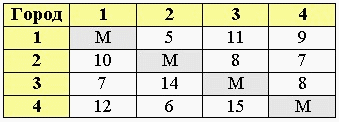
В нашем примере у нас 4 города и в таблице указано расстояние от каждого города к 3-м другим, в зависимости от направления движения (т.к. некоторые ж/д пути могут быть с односторонним движением и т.д.).
Расстояние от города к этому же городу обозначено буквой M. Также используется знак бесконечности. Это сделано для того, чтобы данный отрезок путь был условно принят за бесконечно длинный. Тогда не будет смысла выбрать движение от 1-ого города к 1-му, от 2-ого ко 2-му, и т.п. в качестве отрезка маршрута.
2. Нахождение минимума по строкам
Находим минимальное значение в каждой строке (di) и выписываем его в отдельный столбец.
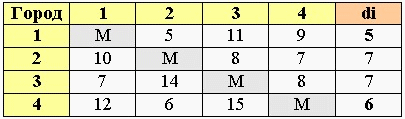
3. редукция строк
Производим редукцию строк – из каждого элемента в строке вычитаем соответствующее значение найденного минимума (di).
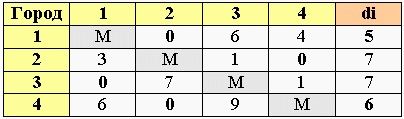
В итоге в каждой строке будет хотя бы одна нулевая клетка.
4. Нахождение минимума по столбцам
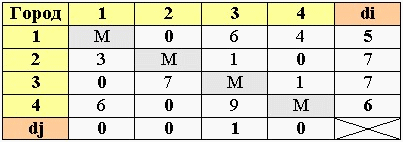
Далее находим минимальные значения в каждом столбце (dj). Эти минимумы выписываем в отдельную строку.
5. редукция столбцов
Вычитаем из каждого элемента матрицы соответствующее ему dj.
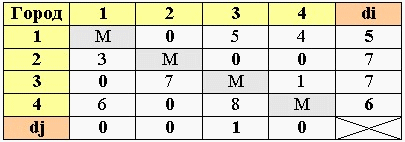
В итоге в каждом столбце будет хотя бы одна нулевая клетка.
6. Вычисление оценок нулевых клеток
Для каждой нулевой клетки получившейся преобразованной матрицы находим «оценку». Ею будет сумма минимального элемента по строке и минимального элемента по столбцу, в которых размещена данная нулевая клетка. Сама она при этом не учитывается. Найденные ранее di и dj не учитываются. Полученную оценку записываем рядом с нулем, в скобках.

И так по всем нулевым клеткам:
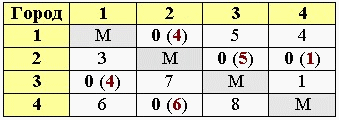
7. редукция матрицы
Выбираем нулевую клетку с наибольшей оценкой. Заменяем ее на «М». Мы нашли один из отрезков пути. Выписываем его (от какого города к какому движемся, в нашем примере от 4-ого к 2-му).
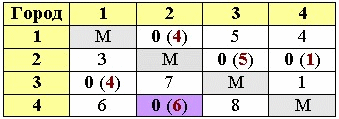
Ту строку и тот столбец, где образовалось две «М» полностью вычеркиваем. В клетку соответствующую обратному пути ставим еще одну букву «М» (т.к. мы уже не будем возвращаться обратно).
8. если полный путь еще не найден, переходим к пункту 2, если найден к пункту 9
Если мы еще не нашли все отрезки пути, то возвращаемся ко 2-му пункту и вновь ищем минимумы по строкам и столбцам, проводим их редукцию, считаем оценки нулевых клеток и т.д.
Если все отрезки пути найдены (или найдены еще не все отрезков, но оставшаяся часть пути очевидна) – переходим к пункту 9.
9. вычисление итоговой длины пути и построение маршрута
Найдя все отрезки пути, остается только соединить их между собой и рассчитать общую длину пути (стоимость поездки по этому маршруту, затраченное время и т.д.). Длины дорог соединяющих города берем из самой первой таблицы с исходными данными.
В нашем примере маршрут получился следующий: 4 → 2 → 3 → 1 → 4.
Общая длина пути: L = 30.
В данной работе мы познакомились с основными понятиями теории графов, дали представление о задаче коммивояжера, описали основные методы оптимизации метод. Также привели пример использования метода ветвей и границ для решения задачи коммивояжера.
Еще раз отметим, что задача коммивояжера является одной из самых важнейших задач в теории графов. Возможность представления различных производственных процессов на языке теории графов и умение решить сформулированную математическую задачу позволяют найти оптимальную стратегию ведения хозяйства, сэкономить ресурсы, выполнить поставленную задачу в более короткие сроки.
Список использованной литературы
1. Кирсанов М.Н. «Графы в Maple», М. Физматлит, 2007.
2. Зыков А.А. «Основы теории графов» , М. «Вузовская книга», 2014
3. Уилсон Р. «Введение в теорию графов» , М. «Мир», 2010
4. Берж К. "Теория графов и ее применение", М., ИЛ, 2008;
5. Гарднер М. "Математические досуги", М. "Мир", 2009(глава 35);
6. "В помощь учителю математики", Йошкар-Ола, 2011 (ст. "Изучение элементов теории графов");
7. Олехник С.Н., Нестеренко Ю.В., Потапов М.К. "Старинные занимательные задачи", М. "Наука", 2008;
8. Гарднер М. "Математические головоломки и развлечения", М. "Мир",2012;
9. Оре О. "Графы и их применения", М. "Мир", 2011;
10. Зыков А.А. "Теория конечных графов", Новосибирск, "Наука", 2009;
11. Реньи А., "Трилогия о математике", М., "Мир", 2010.
Сформулируем задачу.
Дано N узлов, расположенных на плоскости. Задан входной узел (Вх) и выходной узел (Вых). Необходимо обнаружить кратчайший путь, охватывающий все узлы, начинающийся во входном узле, заканчивающийся в выходном узле и проходящий через каждый узел только один раз.
Есть мнения, что задача коммивояжёра может формулироваться ещё двумя способами:
1. Необходимо обнаружить кратчайший гамильтонов цикл.
2. Необходимо обнаружить кратчайший путь, начинающийся в заданном узле.
Однако обе эти формулировки при ближайшем рассмотрении оказываются частными случаями первоначальной формулировки.
Формулировка 1 подразумевает, что входным узлом может быть любой узел, а выходным — один из ближайших к нему. Что требует полного перебора всех ближайших узлов к произвольно выбранному узлу.
Формулировка 2 подразумевает, что входной узел задан, а выходным узлом может быть любой. Что требует полного перебора всех выходных узлов с последующим выбором кратчайшего пути из всех кратчайших.
Поэтому мы остановимся на первоначальной формулировке, и будем решать задачу в общем виде.
Общепризнанно, что задача коммивояжёра в общем случае гарантированно решается оптимально только полным перебором всех вариантов.
В алгоритмической реализации полного перебора возможно применение двух условий, сокращающих время перебора и отсекающих заведомо неоптимальные пути, а именно:
1. При построении очередного варианта пути, подсчитывать его длину и если эта длина превышает уже найденный локальный минимум длины – пропускать этот вариант и все те, которые он порождает.
2. Если следующее выбранное ребро пересекает одно из ранее построенных рёбер – пропустить этот вариант и все те, которые он порождает.
Последнее условие фактически запрещает циклы, т.к. если мы представим себя на месте реального коммивояжёра, то пересечение рёбер (несмотря на то, что в задаче запрещено в явном виде только повторное использование узлов) фактически будет означать возврат коммивояжёра в то место, где он уже был, что противоречит определению оптимального (кратчайшего) пути.
Оптимальное решение задачи коммивояжёра на десктопах возможно. Однако с ростом количества узлов время, затрачиваемое на полный перебор, растёт экспоненциально. Таким образом, на машине с четырёхядерным процессором 2,67 ГГц 10 узлов обсчитывается в среднем за 5 миллисекунд, 20 узлов – за 15 минут, а на расчёт оптимального пути для 60 узлов уйдёт более 6 триллионов лет…
Для обхода этого препятствия люди просто отказываются от получения оптимального решения для больших N и вместо задачи коммивояжёра решают какую-то другую, очень похожую, аналогичную задачу. Такой метод подмены задачи получил название «эвристического решения», хотя эвристика в каждом случае – это не более чем случайно выбранная аналогия. Например, отжиг – это решение задачи путём имитации охлаждения кристаллизующихся веществ, жадный алгоритм – это имитация поведения жадного человека, существуют методы, построенные по аналогии с поведением муравьёв, надувающимся воздушным шариком и т.п.
Метод аналогии плох тем, что полный перебор, как оптимальный метод решения, отбрасывается полностью и полностью заменяется каким-то другим методом. Я считаю, что так пренебрежительно поступать с полным перебором нельзя, потому что это единственный метод, который гарантированно даёт правильное решение задачи.
Мы попробуем решать задачу коммивояжёра только полным перебором, заменяя его чем-то другим только там, где это действительно необходимо из соображений экономии времени.
Мы не будем искать аналогию наугад, мы попробуем решить задачу коммивояжёра максимально непредвзято, не призывая на помощь посторонние аналогии. Попробуем решить общую задачу в общем виде. А для этого призовём на помощь только одну аналогию — аналогию с интеллектом вообще. Как решает сложные задачи (в том числе и задачу коммивояжёра) человеческий интеллект? Он разбивает исходную задачу на дерево более простых под-задач, решает их в обратном порядке и получает результат. Мы поступим точно так же!
Совершенно очевидно, что упростить задачу коммивояжёра для того, чтобы решать её полным перебором за приемлемое время, можно только одним способом – уменьшить количество перебираемых узлов. А это возможно сделать тоже только одним способом – объединить узлы в группы – над-узлы, над-задачи (суб-задачи).
Чтобы поставить задачу коммивояжёра рекурсивно попробуем взглянуть на неё рекурсивно.
Основной элемент в этой задаче – это узел, в который входит одно ребро и выходит одно ребро:
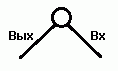
Не призывая посторонние аналогии, мы тут же замечаем аналогию с самой постановкой общей задачи, в которой задано два «крайних» узла: Вх, в который входит коммивояжёр на старте, и Вых, из которого выходит коммивояжёр на финише. Можно сказать, что вся совокупность узлов N в задаче – это один большой узел, в который коммивояжёр входит и выходит по ребру:
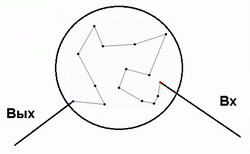
Таким образом, вырисовывается общий вид рекурсивного алгоритма.
1. Задать узлы N.
2. Задать максимально допустимое время решения задачи Tmax.
3. Провести на данной машине бенчмарк и определить зависимость времени решения от количества узлов при полном переборе вариантов Т(N).
4. Исходя из заданного количества узлов N, Tmax и зависимости для Т определить, на сколько групп (над-узлов) следует разбить множество из N узлов. Либо задать это количество узлов вручную (именно так мы и поступим).
5. Разбить множество из N узлов на M групп.
6. Провести полный перебор для M групп и найти кратчайший путь для соединения этих групп.
7. После шага 6 у нас известно для каждой группы вход и выход, поэтому мы ставим рекурсивно задачу коммивояжёра для каждой группы, т.е. переходим к шагу 4, где N равно количеству узлов в каждой группе.
8. После выхода из рекурсии получаем подоптимальный путь для данной машины и данного Tmax (либо заданного количества узлов в группе).
Пункт 4 нужен для того, чтобы мы не ухудшали алгоритм сверх необходимого. Если машина может провести полный перебор для данного количества узлов, то мы должны ей это позволить.
На шаге 5, очевидно, лучше предпочитать M как можно больше. При М стремящемся к N мы получаем всё более точное решение. Чем меньше мы уходим от полного перебора, тем точнее наше решение. Выбрать M можно по таблице, составленной из самого простого грубого предположения, что на каждом шаге рекурсии мы будем разбивать суб-задачу на группы с одинаковым количеством узлов в группе.
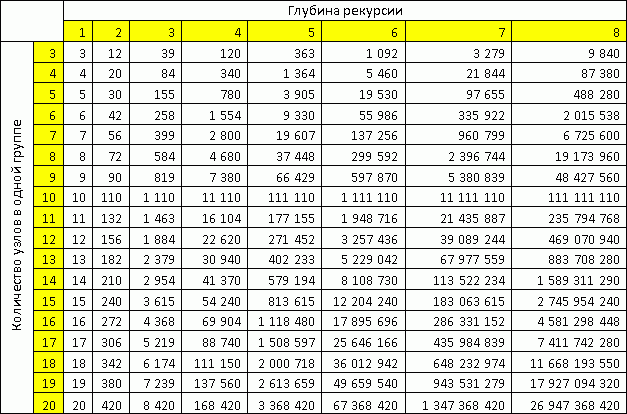
Как видно из таблицы, уже при 18 узлах в одной группе мы можем обрабатывать более 10 миллиардов узлов при глубине рекурсии до 8.
Если мы хотим улучшить найденный таким образом маршрут, то у нас есть такие варианты:
— выбрать более производительную машину
— увеличить допустимое время Tmax
— увеличить количество групп
— увеличить вложенность рекурсии. То есть на шаге 6 разбивать задачу на существенно (в зависимости от N) большее число групп, но производить их перебор не оптимально, а подоптимально. Например, разбивать задачу из 1000 узлов на 500 групп, но искать не кратчайший путь их соединения полным перебором (это слишком долго), а разбивать группы на суб-группы, например по 250 групп и проводить поиск подоптимального пути среди них. И так далее, пока мы не спустимся на уровень, где машина может сделать полный перебор.
Как объединять узлы в группы?
Чтобы не привлекать отвлечённые аналогии и не пользоваться туманными эвристиками, попробуем найти ответ в самой задаче. Совершенно ясно, что изначально в задаче у нас одна группа, для которой заданы Вх и Вых.
Чтобы разбить данную задачу минимум на две, нам необходимо выделить среди всех узлов промежуточный узел, который станет промежуточным входом/выходом.
Поскольку в качестве признака оптимальности в задаче мы применяем евклидово расстояние, то для обнаружения нового промежуточного входа/выхода нам необходимо ввести некий лимит расстояния от каждого узла до уже существующих входа и выхода. Поскольку мы не знаем, что это за лимит мысленно возьмём его настолько большим, чтобы оказалось, что все узлы принадлежат только начальной группе. Теперь мысленно будем плавно уменьшать этот лимит. При этом один из узлов, ранее принадлежавший первоначальной группе, должен выделиться из неё. Независимо от того, что именно мы возьмём в качестве лимита, этим узлом станет тот узел, который расположен на самом дальнем расстоянии от первоначальных входа и выхода. Поэтому вместо выдумывания формулы лимита мы можем сразу брать самый дальний узел. После того как мы нашли этот промежуточный вход/выход, мы должны поделить все оставшиеся узлы между новыми двумя группами так, чтобы гарантировать непересечение ребёр.
Если нам надо поделить задачу на произвольное число групп, то мы производим это разбиение рекурсивно. Сначала находим промежуточный вход/выход взаимо-дальний по отношению к начальным входу и выходу. Потом находим второй промежуточный вход/выход взаимо-дальний к первым трём, и так далее.
Очевидно, что при количестве групп, равному N, промежуточные входы/выходы этих групп совпадут с начальными узлами. Таким образом, мы нашли единственно правильное деление всех узлов на группы.
Поэкспериментировать с разбиением на группы можно здесь (исходные коды Object Pascal прилагаются).
Чтобы создать задачу коммивояжёра нужно ввести количество узлов и нажать Enter. Либо загрузить задачу из файла.
Перемещая ползунок можно наблюдать принцип разбиения на группы. Кнопка «Link groups» соединяет текущие группы по оптимальному маршруту полным перебором. Кнопка «Link nodes» соединяет все узлы по оптимальному маршруту полным перебором. Поэтому не следует нажимать эти кнопки при большом (>18) количестве узлов или групп.
Здесь можно скачать программу и исходные коды для решения задачи коммивояжёра по алгоритму, описанному выше.
Органы управления:
Кнопка «Load» загружает задачу из файла с расширением *.txt
Формат файла txt такой: в каждой строке через 1 пробел указаны координаты x и y для каждого узла в задаче. В первой строке указаны координаты входного узла. В последней строке – координаты выходного узла. Остальные узлы между ними в произвольном порядке. Координаты находятся в диапазоне 0-1 с точностью 6 знаков после запятой. Отделитель целой и дробной части – запятая.
Кнопка «Generate» генерирует случайную задачу коммивояжёра, с количеством узлов, указанном в поле «Nodes».
Кнопка «Save» сохраняет координаты узлов данной задачи.
Кнопка «Solve» решает задачу коммивояжёра, рекурсивно разбивая её на константное количество групп, указанном в поле «Groups». Если заданное количество групп больше либо равно количеству узлов, то будет, естественно, производится полный перебор узлов. Поэтому не рекомендуется указывать количество групп более 18.
В данной программе разбивка на группы не оптимальная, поэтому пересечения случаются. Но этот недостаток принципиально устраним.
Для улучшения алгоритма следует разделить параметр Nodes на два независимых параметра:
Nmax — максимальное количество узлов, для которого делается полный перебор без разбиения на группы.
Gmax — количество групп для разбиения узлов, количество которых превысило Nmax. И это число можно задавать по разному. Можно делить количество узлов на константу, можно отнимать 1 от текущего количества узлов, можно делить количество узлов в пропорции «золотого сечения», можно брать фиксированный процент. На этот счёт мною ведутся исследования.
В данной программе, для простоты и наглядности Gmax = Nmax = Groups.
Одну тысячу узлов при Groups=13 программа просчитывает менее чем за 5 секунд. Для полного перебора результат очень хороший.
Общие сведения
Может быть, алгоритм, основанный на полном переборе вариантов, не является самым эффективным (в смысле быстродействия) для решения задачи коммивояжёра? Увы, доказано, что не существует алгоритма решения, имеющего степенную сложность (то есть требующего порядка n a операций для некоторого a ) — любой алгоритм будет хуже. Всё это делает задачу коммивояжёра безнадёжной для ЭВМ с последовательным выполнением операций, если n хоть сколько-нибудь велико.
В таком случае следует отказаться от попыток отыскать точное решение задачи коммивояжёра и сосредоточиться на поиске приближённого — пускай не оптимального, но хотя бы близкого к нему. В виду большой практической важности задачи полезными будут и приближённые решения.
Заметим, что интеллект человека, не вооружённый вычислительной техникой, способен отыскивать такие приближённые решения задач, требующих огромного перебора вариантов в поисках оптимального. Вспомним хотя бы шахматы. Человек может весьма успешно соперничать в этой игре с вычислительной машиной либо вовсе не прибегая к перебору, либо сводя его к минимуму. Человек руководствуется при этом интуицией и набором эвристик (находок) — правил, которые обычно помогают в решении задач, хотя эффективность таких правил и не имеет достаточного обоснования. В качестве подобной универсальной эвристики можно упомянуть категорический императив Канта: «поступай с другими так, как тебе хотелось бы, чтобы поступали с тобой». Другой, более приземлённый пример даёт золотое правило валютного спекулянта: «когда все продают доллары, ты покупай, а когда все покупают — продавай».
Задачи комбинаторной оптимизации
Переборные задачи, нацеленные на поиск оптимального варианта, называют задачами комбинаторной оптимизации.
Задача коммивояжёра может быть поставлена как задача оптимизации. В качестве множества X достаточно взять S n (множество перестановок n -элементного множества), а в качестве целевой функции U x — длину замкнутой ломаной, проходящей через n заданных точек в порядке, заданной перестановкой x ∈ X .
Метод градиентного спуска
Для множеств X , для которых определено отношение близости, годятся и другие методы. Среди них — метод градиентного спуска.
Отношение близости — это способ определить для двух элементов множества, являются ли они близкими (в каком-нибудь смысле). Для числовых множеств, для множеств точек на плоскости или в пространстве близкими можно считать два числа (две точки), расстояние между которыми не превосходит некоторого маленького числа ε . Для множества S n близкими удобно считать две перестановки, отличающиеся на одну транспозицию, то есть получающиеся друг из друга «рокировкой» двух элементов множества. Например, перестановки 2 4 1 3 и 2 3 1 4 являются близкими в этом смысле, так как отличаются перестановкой элементов с номерами 2 и 4 . Можно определить и более строгое отношение близости, при котором близкие перестановки отличаются на соседнюю транспозицию, когда рокировка затрагивает элементы множества с соседними номерами. Тогда указанные выше перестановки близкими уже не будут, но близкими окажутся 2 4 1 3 и 2 4 3 1 .
Суть метода градиентного спуска отражена в его названии и заключается в следующем. Строится последовательность x 0 x 1 x 2 x 3 … ⊂ X , в которой начальный элемент x 0 выбирается произвольно (возможно, случайным образом), а каждый последующий является одним из соседей предыдущего, причём именно тем из соседей, для которого значение функции U будет наименьшим. Построение последовательности завершается тогда, когда последовательность значений целевой функции U x 0 U x 1 U x 2 U x 3 … перестанет быть монотонно убывающей.
Имеется вероятностная версия метода градиентного спуска. На каждом шаге для элемента множества X выбирается случайный сосед. Если значение целевой функции в случайной соседней точке уменьшилось, она добавляется в последовательность, и мы переходим к следующему шагу. Если же нет, то снова выбирается случайный сосед. Алгоритм останавливается, если достаточно долго не пополняется последовательность (не происходит переход к следующему шагу): вероятно, алгоритм в этом случае привёл в точку локального минимума.
Метод имитации отжига
Метод имитации отжига является модификацией вероятностного метода градиентного спуска. Отличие заключается в поведении алгоритма, когда U x ⩽ U x ˜ , где x — очередной элемент последовательности, а x ˜ — его сосед, выбранный наугад. Вероятностный метод градиентного спуска отвергал такого соседа безусловно, а метод имитации отжига допускает добавление такого «плохого» соседа в последовательность, правда, с некоторой вероятностью p , зависящей от того, насколько плохой сосед ухудшил целевую функцию. Возьмём разность ∆ U = U x ˜ − U x (она неотрицательна, если сосед «плохой») и положим p = e − ∆ U Θ . Здесь e — некоторое число, большее единицы (какое именно, не принципиально, но обычно берут e ≈ 2,718281828459045… — основание натуральных логарифмов), а Θ — некоторое положительное число, называемое температурой.
На рисунке 45.1. «Вероятность мутации для метода имитации отжига» показаны зависимости вероятности мутации от величины ∆ U при различных значениях температуры Θ . Высоким температурам соответствуют графики, чей цвет ближе к красному, низким — к синему. Как и положено, значение вероятности заключено в отрезке 0 1 . При отрицательных ∆ U вероятность равна 1 , что соответствует случаю «хорошей» мутации.

Приложение на рисунке 45.2 позволяет понаблюдать за процессами, присходящими при поиске оптимального решения задачи коммивояжёра методом имитации отжига.
| Примечание | |
|---|---|
