Частотность — термин лексикостатистики, предназначенный для определения наиболее употребительных слов. Расчёт осуществляется по формуле:
F r e q x = Q x Q a l l ,
где Freqx — частотность слова «x», Qx — количество словоупотреблений слова «x», Qall — общее количество словоупотреблений. В большинстве случаев частотность выражается в процентах. В словарях частотность слов может отражаться пометками — употребительное, малоупотребительное и т. д.
Аналогичным образом определяется частотность для букв. Бо́льшая частотность согласных на данном отрезке текста (например, в стихотворениях) получила название аллитерации. Высокие показатели частотности гласных называются ассонансом. Частотный анализ используется в криптографии для выявления наиболее частотных букв того или иного языка.
Частотность слов и букв являлась важнейшим инструментов криптоанализа в эпоху до повсеместного распространения блочных шифров.
Не следует путать термины частотность и частота.
Частотность букв русского языка [ править | править код ]
Статистика частотности букв русского языка (на материале НКРЯ): [1]
Таблица 8.4
Таблица 8.2
Таблица 8.1
| События, обстоятельства, факты | Год | |||
| Убийств вообще | ||||
| Ружье и пистолет | ||||
| Сабля, шпага, стилет, кинжал и т. п. | ||||
| Нож | ||||
| Палка, трость и т. п. | ||||
| Камень | И | |||
| Орудия режущие, колющие и ушибающие | ||||
| Удушения | ||||
| Сбрасывание и утопление | ||||
| Удар ногой и кулаком | ||||
| Огонь | – | – | – | – |
| Убийство от неизвестных орудий | – |
Определенное постоянство числа фактов свойственно, конечно, не только «удушениям и утоплениям». Вот еще одна таблица, на этот раз полученная на основании статистических данных по городу Берлину в начале нашего века (табл. 8.2).
| События, обстоятельства, факты | Год |
| Несчастные случаи в воскресенье | |
| Несчастные случаи | |
| в понедельник | |
| Вдовы, в третий раз вступившие в брак | |
| Вдовы, в четвертый раз вступившие в брак | |
| Переезды на другую квартиру в октябре | 134 202 |
| Переезды на другую | |
| квартиру в ноябре | |
| Извозчики, отъехавшие | |
| с седоками от Потсдамского вокзала | |
| Извозчики, отъехавшие | |
| с седоками от Герлицкого | |
| вокзала |
Что может, казалось бы, быть дальше от каких-либо правил, чем вступление в брак? Случайна обычно сама встреча будущих супругов. От многих трудноуловимых обстоятельств зависит, решат ли они связать свои жизни, – без раздумий и сомнений дело, как правило, не обходится. Внешность, характер – все тут имеет значение. Однако, как видно из таблицы, даже в таком событии, как брак, явно просматриваются железные регулярности, непреложные правила.
Закономерности в случайных явлениях были издавна подмечены и использованы людьми, в частности, для предсказания погоды по так называемым народным приметам. Существует, например, примета, по которой в первых числах августа – в Ильин день – увеличивается количество гроз («Илья Пророк в золотой колеснице по небу катается»). Метеорологи в результате почти сорокалетних наблюдений составили любопытную таблицу (табл. 8.3).
| Дата | 31.VII | 1.VIII | 2.VIII | 3.VIII | 4.VIII | 5.VIII |
| Число гроз |
Таблица не оставляет сомнения в точности народных примет: в первых числах августа количество гроз действительно резко увеличивается. Так рождались безошибочные предсказания.
Одним из первых ученых, отметивших закономерности в массовых случайных явлениях был великий французский ученый П. Лаплас (кстати, А. Кетле был его учеником). Лаплас просмотрел метрические книги города Парижа с записями о рождении детей с 1745 года (в этом году впервые начали отмечать в книгах пол младенца) по 1884 год. За это время было зарегистрировано 393 386 мальчиков и 377 555 девочек. Таким образом, на каждые 25 мальчиков приходилось примерно по 24 девочки. Между тем Лаплас знал, что во Франции, а также в большинстве стран Европы и Америки это отношение составляет 22 и 21. Предоставим поэтому повсюду слово самому Лапласу: «Когда я стал размышлять об этом, то мне показалось, что замеченная разница зависит от того, что родители из деревни и провинции оставляют при себе мальчиков (мужчина в хозяйстве – более ценная рабочая сила), а в приют для подкидышей отправляют девочек». Изучив списки парижских детских приютов, Лаплас убедился в справедливости своего предположения: в случайном соотношении полов новорожденных просматривалась железная закономерность.
Итак, в сложных запутанных массовых явлениях, зависящих от необозримого множества случайных причин, случайность как бы перестала быть случайной. Неопределенность уступает место определенности. Вывод этот настолько ошеломлял, что знаменитый статистик К. Пирсон не поленился бросить монету 24 000 раз и. получил 12012 «гербов», что дает частоту, весы близкую к 0,5. Закономерность и здесь оказалась вполне определенной.
Произведем и мы не менее поучительный эксперимент.
Предложите вашему знакомому придумать свой личный шифр – каждая буква алфавита заменяется каким-либо «хитрым» значком: точкой, кружочком, треугольником и т. п. – и написать этим, известным только ему одному, шифром письмо вам на одной-двух страницах. Ручаюсь за эффект после того, как вы через некоторое время огласите расшифрованный текст письма.
Секрет этого «фокуса» в том, что в случайном, казалось бы, наборе букв «шифровки» проявляется строгая регулярность: частота появления каждой из букв алфавита в тексте является практически постоянной. Приведем эти данные (табл. 8.4).
| Буква | Частота | Буква | Частота | Буква | Частота |
| а | 0,075 | К | 0,034 | Ф | 0,002 |
| б | 0,017 | л | 0,042 | X | 0,011 |
| в | 0,046 | м | 0,031 | ц | 0,005 |
| г | 0,016 | и | 0,065 | ч | 0,015 |
| д | 0,030 | о | 0,110 | ш | 0,007 |
| е, ё | 0,087 | II | 0,028 | щ | 0,004 |
| ж | 0,009 | р | 0,048 | ь, ъ | 0,017 |
| 0,018 | с | 0,055 | ы | 0,019 | |
| и | 0,075 | т | 0,065 | э | 0,003 |
| и | 0,012 | у | 0,025 | ю | 0,022 |
| я | 0,022 |
Из таблицы следует, что на каждую тысячу букв в среднем приходится 75 букв а, 17 букв б, 46 букв в и т. д.
Получив шифрованное письмо, вам придется лишь подсчитать частоты появления в нем различных секретных значков и сопоставить их с теми частотами, что в таблице. Так, если на тысячу восемьсот букв письма окажется 135 «треугольников», то это означает, что данный значок

А вот еще один эксперимент – специально для любителей «счастливых» билетов. (Как известно, «счастливым» считается такой трамвайный, автобусный, троллейбусный билет, у которого сумма первых трех цифр равна сумме трех последних). В теории вероятностей существует формула, в соответствии с которой на каждые 100 билетов в среднем 5–6 должны оказаться «счастливыми». И если не полениться собрать необходимую пачку в сто билетов, то можно легко в этом убедиться.
«Обязательность» случая была давно подмечена предприимчивыми людьми.
В чем смысл игры для хозяина рулетки? Главный «секрет производства» здесь в том, что выпадение цифры 0 – ее называют «зеро» – всегда в пользу хозяина, независимо от того, на «красное» или «черное» поставил игрок свои деньги. За счет этой единственной цифры и существует хозяин рулетки. И не только он. Целое государство Монако живет за счет доходов знаменитого игорного дома в Монте-Карло, где идет крупная игра в рулетку. Трудно придумать более яркий пример использования закономерностей случайных явлений: выход «зеро» определенное число раз столь же обязателен, как, скажем, падение подброшенного камня на землю, хотя каждая отдельная цифра появляется случайно и никакими силами заранее угадана быть не может.
И все же Смок Беллью, герой повести Джека Лондона, если вы помните, научился почти безошибочно предугадывать, где остановится шарик. Как ему это удавалось делать?
Джек Лондон раскрывает секрет своего любимого героя. Наблюдая за игрой, Смок подметил, что колесо останавливалось не как попало – этого, казалось бы, следовало ожидать, – а по определенным правилам. «Случайно я дважды отметил, где остановился шарик, когда вначале против него был номер девять. Оба раза выиграл двадцать шестой». Столь странное поведение колеса объяснялось тем, что рулетка стояла недалеко от печки: ее деревянное колесо рассохлось и покоробилось. Смоку удалось уловить скрытую от других закономерность поведения колеса.
Стоит ли, однако, утверждать, что можно выявить систему у любых – всех проявлений случая? Попробуйте, например, установить общие закономерности изменения моды, формы одежды, которая, безусловно, относится к случайным явлениям. На рис. 8.1 показаны колебания мод женской одежды почти за 50 лет XX века. Срок вполне достаточный, чтобы найти хоть какие-нибудь основательные регулярности. Однако их нет. Все – и форма шляпок, и силуэт платья – меняются «как попало». Остается незыблемым лишь общий принцип: «новое – это прочно забытое старое». Предпринимавшиеся попытки связать капризы моды с мировыми катаклизмами – войнами, экономическими кризисами, даже с солнечной активностью – ни к чему не привели.

Рис. 8.1.Динамика дамской моды
Возможность установления определенного порядка, закономерностей в случайных явлениях, как правило, связана с наличием в них так называемой «устойчивой частоты»: появление интересующего нас события, например рождение младенца мужского пола, при многократном повторении происходит в одинаковой доле от общего числа рождений.
Поисками закономерностей в случайных явлениях занимается специальная, хорошо разработанная в наши дни наука – статистика. Именно статистика после многих наблюдений над случаем делает заключение о том, устойчива ли частота его появления. Когда такую устойчивость удается обнаружить, статистики говорят о наличии статистического ансамбля.
Изучением закономерностей в случайных явлениях занимается теория вероятностей. Познакомимся с основами этой науки.
Как и многие другие понятия, слово «вероятность» с его производным «вероятно» входит в нашу жизнь с детства. Мы говорим: вероятно, вечером будет дождь; я, вероятно, простудился и т. п.
« Вероятно» в этих привычных фразах означает «возможно» – этим словом субъективно оценивается возможность наступления интересующего нас случайного события в будущем. Если же появляется необходимость показать степень этой возможности, мы уточняем: «весьма вероятно», «маловероятно», «совершенно невероятно». Более четкие градации, чем «много» и «мало», в обиходном языке не предусмотрены. Между тем жизненные задачи требуют оценки вероятности более конкретной, чем «много» или «мало». Сегодня на морском транспорте сказать: вероятно, будет (или не будет) происшествие – это значит не сказать почти ничего. Степень возможности появления будущего случайного события – вероятность – должна быть оценена объективно точно, определенным числом.
Самый старый, так называемый классический способ измерения вероятности – по частоте наступления интересующего нас события. Это можно сделать весьма просто: прийти в тир, выстрелить все 100 раз и сосчитать число попаданий в мишень. Доля, которую это число составит от общего числа выстрелов, и есть частота попаданий. Скажем, попали 70 раз – частота равна 0,7, или семидесяти процентам. Вот эта самая частота и принимается за вероятность.
Но что значит «принимается»? Почему не сказать просто: вероятность – это и есть частота интересующего нас события? По той же самой причине, по которой мы различаем вчерашнюю сводку погоды и прогноз на завтра. Частота -это результат события, которое уже произошло, вероятность – предсказание того, что должно случиться в будущем. Сказать: «Вероятность попадания 70 процентов» – значит предположить, что при очередной стрельбе 70 пуль из ста попадут в мишень. Это предположение мы делаем в уверенности, что соотношение шансов попасть – не попасть, которое определилось во время уже состоявшейся стрельбы, сохранится и на будущее. При этом, разумеется, предполагается, что условия стрельбы: оружие, расстояние до мишени, размеры мишени и т. д. – останутся неизменными.
Применительно к бизнесу это означает, что если при определенных условиях в прошлом мы получали, на каждые 100 рублей 30 рублей прибыли, то при повторении ситуации в будущем сохранится и прибыль.
Откуда, однако, у нас берется уверенность, что «дальше будет, как раньше»? К этому нас подводит весь многовековой коллективный опыт человечества. Когда народ говорит, например, «У семи нянек дитя без глаза», «Тише едешь – дальше будешь» или утверждается, что «бутерброд падает маслом вниз», – это не только о прошлом, но и о будущем.
Если в течение многих лет люди наблюдают, как из 100 куриных яиц появляется примерно поровну петушков и курочек, то нет основания не верить, что и на следующий год шансы появления петушка останутся прежними. В слове «вероятно» явственно прослушивается «надеюсь». Это дало основание магистру философии Вильнюсского университета Сигизмунду Ревковскому – первому, кто в 1829– 1830 годах стал преподавать в России (тогдашней) теорию вероятностей, – определить вероятность как «меру надежды».
Итак, для того чтобы рассчитать вероятность во многих распространенных жизненных задачах, достаточно произвести весьма элементарное арифметическое вычисление – разделить число случаев, благоприятствующих интересующему нас событию, на общее число всех возможных случаев.

Важно отметить, что чем больше опытов проведено при определении частоты, тем точнее, объективнее получается вероятность. Это проявление одного из важнейших законов, управляющих случаем, – так называемого закона больших чисел.
Классический способ определения вероятностей и его формула и сегодня находят широкое применение. Если нам, скажем, известно, что среди тридцати экзаменационных билетов три очень трудных, то можно быстро прикинуть вероятность вытащить трудный билет, как  = 0,1, или 10 процентов. И если бы можно было таким простым способом рассчитывать вероятности во всех случаях, то учебники по теории вероятностей (а заодно и данная глава) были бы много тоньше. К большому сожалению, столь просто рассчитывать вероятность удается далеко не всегда.
= 0,1, или 10 процентов. И если бы можно было таким простым способом рассчитывать вероятности во всех случаях, то учебники по теории вероятностей (а заодно и данная глава) были бы много тоньше. К большому сожалению, столь просто рассчитывать вероятность удается далеко не всегда.
Представьте себе, что вы получили перед какой-либо жеребьевкой весьма обнадеживающую информацию: организатор кладет плохие билеты не как попало, а снизу, видно стараясь, чтобы они оказались подальше от испытуемых. Это, конечно, хорошо: стоит теперь вытянуть билет сверху – и вероятность заполучить выгодный номер резко увеличится. Но вот какой она станет? Узнать это с помощью классической формулы невозможно. Формула применима лишь тогда, когда все рассматриваемые случаи равновозможны – любой билет должен иметь одинаковые шансы попасть в руки испытуемого. Стоит исключить эту равновозможность, и классическая формула перестает работать. Следовательно, правильно эту формулу записать так:
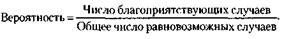
Откуда же мы знаем, равновозможны случаи или нет? На этот вопрос отвечает опыт.Причем опыт, который не обязательно ставить. Бывает, вполне достаточно провести его мысленно. Допустим, вы собрались сыграть с товарищем в шахматы. Кому играть белыми, должен решить жребий. Ваш партнер в одной руке зажимает белую фигуру, в другой – черную. Какова вероятность, что вы будете играть белыми? Каждый из нас, не задумываясь, назовет 50 процентов. Но почему? Это результат мысленного опыта: мы инстинктивно оцениваем шансы отгадать любую фигурку как равновероятные, и поскольку белых фигур ровно половина, то это и будет интересующая нас вероятность.
Вот еще один пример. Многим читателям, видимо, доводилось слышать о такой дикой игре армейского захолустья царской России. В барабан многозарядного револьвера закладывается лишь один патрон, после чего барабан несколько раз проворачивается. Затем участники игры по очереди приставляют револьвер к виску и нажимают на спуск. Так вот, для того чтобы сказать, чему равна при этом вероятность проигрыша, явно нет необходимости ставить эксперимент. Так же как и при отгадывании шахматной фигуры, равновозможность шансов здесь очевидна из соображения о симметрии возможных исходов. И вероятность проигрыша – получения пули – для того, кто стреляет первым, в расчете на 5 патронов равна:
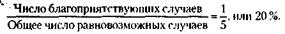
Вполне можно ограничиться мысленным экспериментом и там, где равновозможность шансов очевидна из геометрического представления задачи. Скажем, в офисе проложен телефонный кабель длиной 60 метров, из которых 3 метра приходится на труднодоступное место. Спрашивается, какова вероятность в случае выхода кабеля из строя, что повреждение случится именно на труднодоступном участке?

Такую вероятность иногда называют геометрической – ведь она получена путем сопоставления длин двух отрезков. И соображение о равновозможности шансов (уверенность в том, что появление неисправности возможно в любом месте кабеля) в этом случае исходит из наглядных, геометрических представлений.
Интуитивное определение вероятности, выработанное человеком и ходе многовековой эволюции, не раз выручало его в сложных ситуациях. Принимая решение «что лучше», «что быстрее», «какова мера опасности», люди, сами того не ведая, часто основывают свой выбор на интуитивной вероятной оценке. «Лучше поездом, чем самолетом», «Поеду-ка я трамваем, автобуса не дождаться», «Сегодня стоит надеть плащ» – во всех этих решениях явно просматривается учет возможности случая.
С интуитивным определением вероятности тесно связан так называемый принцип практической уверенности. Принцип этот можно сформулировать так: «Если вероятность события мала, то следует считать, что в однократном опыте – в данном конкретном случае – это событие не произойдет. И наоборот – при большой вероятности событие следует ожидать».
В повседневной жизни мы широко, сами то не подозревая, пользуемся этим важным принципом. Скажем, собираясь лететь в отпуск самолетом, мы уверены в том, что нас доставят на места в целости и сохранности: не пишем завещание, даем телеграмму с просьбой встретить т. п. Тем самым мы интуитивно принимаем, что вероятность аварии самолета равна нулю – событие невозможное, хотя эта вероятность всегда имеет некоторое, правда весьма небольшое, но все же отличное от нуля значение. Вероятность же нашей доставки до места соответственно но принимается равной единице – событие это считается достоверным.
Оценивая практическую невозможность или достоверность события и принимая на этой основе решение, мы, однако, далеко не всегда связываем свой выбор с предельными, крайним значениями вероятности. Величина вероятности, которая нас практически устраивает, зависит от того, какова важность последствий принятого нами решения. Решение надеть плащ может быть принято и в том случае, если вероятность дождя, скажем, 70–80 %. Но вряд ли мы решимся прыгнуть с парашютом, узнав, что у него такая же (70–80 %) надежность.
Итак, вероятность– это степень возможности появления будущего случайного события Руководствуясь этим определением, решим несколько примеров.
Не нашли то, что искали? Воспользуйтесь поиском:
На этом шаге мы рассмотрим информацию и алфавит .
Рассматривая формы представления информации, мы отметили то обстоятельство, что, хотя естественной для органов чувств человека является аналоговая форма, универсальной все же следует считать дискретную форму представления информации с помощью некоторого набора знаков. В частности, именно таким образом представленная информация обрабатывается компьютером, передается по компьютерным и некоторым иным линиям связи. Сообщение есть последовательность знаков алфавита. При их передаче возникает проблема распознавания знака: каким образом прочитать сообщение, т.е. по полученным сигналам установить исходную последовательность знаков первичного алфавита. В устной речи это достигается использованием различных фонем (основных звуков разного звучания), по которым мы и отличает знаки речи. В письменности это достигается различным начертанием букв и дальнейшим нашим анализом написанного. Как данная задача может решаться техническим устройством, мы рассмотрим позднее. Сейчас для нас важно, что можно реализовать некоторую процедуру (механизм), посредством которой выделить из сообщения тот или иной знак. Но появление конкретного знака (буквы) в конкретном месте сообщения – событие случайное. Следовательно, узнавание (отождествление) знака требует получения некоторой порции информации. Можно связать эту информацию с самим знаком и считать, что знак несет в себе (содержит) некоторое количество информации. Попробуем оценить это количество.
Начнем с самого грубого приближения (будем называть его нулевым, что отражается индексом у получаемых величин) – предположим, что появление всех знаков (букв) алфавита в сообщении равновероятно. Тогда для английского алфавита ne=27 (с учетом пробела как самостоятельного знака); для русского алфавита nr=34 . Из формулы Хартли находим:
Получается, что в нулевом приближении со знаком русского алфавита в среднем связано больше информации, чем со знаком английского. Например, в русской букве "а" информации больше, чем в "a" английской! Это, безусловно, не означает, что английский язык – язык Шекспира и Диккенса – беднее, чем язык Пушкина и Достоевского. Лингвистическое богатство языка определяется количеством слов и их сочетаний, а это никак не связано с числом букв в алфавите. С точки зрения техники это означает, что сообщения из равного количества символов будет иметь разную длину (и соответственно, время передачи) и большими они окажутся у сообщений на русском языке.
В качестве следующего (первого) приближения, уточняющего исходное, попробуем учесть то обстоятельство, что относительная частота, т.е. вероятность появления различных букв в тексте (или сообщении) различна. Рассмотрим таблицу средних частот букв для русского алфавита, в который включен также знак "пробел" для разделения слов (из книги А.М. и И.М.Ягломов [с.238]); с учетом неразличимости букв "е" и "ë", а также "ь" и "ъ" (так принято в телеграфном кодировании), получим алфавит из 32 знаков со следующими вероятностями их появления в русских текстах:
Для оценки информации, связанной с выбором одного знака алфавита с учетом неравной вероятности их появления в сообщении (текстах) можно воспользоваться формулой (1.14). Из нее, в частности, следует, что если pi – вероятность (относительная частота) знака номер i данного алфавита из N знаков, то среднее количество информации, приходящейся на один знак, равно:
Это и есть знаменитая формула К.Шеннона , с работы которого "Математическая теория связи" (1948) принято начинать отсчет возраста информатики, как самостоятельной науки. Объективности ради следует заметить, что и в нашей стране практически одновременно с Шенноном велись подобные исследования, например, в том же 1948 г. вышла работа А.Н.Колмогорова "Математическая теория передачи информации" .
Применение формулы (1.17) к алфавиту русского языка дает значение средней информации на знак I1 (r) = 4,36 бит, а для английского языка I1 (e) = 4,04 бит, для французского I1 (l) = 3,96 бит, для немецкого I1 (d) = 4,10 бит, для испанского I1 (s) = 3,98 бит. Как мы видим, и для русского, и для английского языков учет вероятностей появления букв в сообщениях приводит к уменьшению среднего информационного содержания буквы, что, кстати, подтверждает справедливость формулы (1.7). Несовпадение значений средней информации для английского, французского и немецкого языков, основанных на одном алфавите, связано с тем, что частоты появления одинаковых букв в них различаются.
В рассматриваемом приближении по умолчанию предполагается, что вероятность появления любого знака в любом месте сообщения остается одинаковой и не зависит от того, какие знаки или их сочетания предшествуют данному. Такие сообщения называются шенноновскими (или сообщениями без памяти).
Сообщения, в которых вероятность появления каждого отдельного знака не меняется со временем, называются шенноновскими , а порождающий их отправитель – шенноновским источником .
Если сообщение является шенноновским, то набор знаков (алфавит) и вероятности их появления в сообщении могут считаться известными заранее. В этом случае, с одной стороны, можно предложить оптимальные способы кодирования, уменьшающие суммарную длину сообщения при передаче по каналу связи. С другой стороны, интерпретация сообщения, представляющего собой последовательность сигналов, сводится к задаче распознавания знака, т.е. выявлению, какой именно знак находится в данном месте сообщения. А такая задача, как мы уже убедились в предыдущем шаге, может быть решена серией парных выборов. При этом количество информации, содержащееся в знаке, служит мерой затрат по его выявлению.
Последующие (второе и далее) приближения при оценке значения информации, приходящейся на знак алфавита, строятся путем учета корреляций, т.е. связей между буквами в словах. Дело в том, что в словах буквы появляются не в любых сочетаниях; это понижает неопределенность угадывания следующей буквы после нескольких, например, в русском языке нет слов, в которых встречается сочетание щц или фъ. И напротив, после некоторых сочетаний можно с большей определенностью, чем чистый случай, судить о появлении следующей буквы, например, после распространенного сочетания пр- всегда следует гласная буква, а их в русском языке 10 и, следовательно, вероятность угадывания следующей буквы 1/10, а не 1/33. В связи с этим примем следующее определение:
Сообщения (а также источники, их порождающие), в которых существуют статистические связи (корреляции) между знаками или их сочетаниями, называются сообщениями (источниками) с памятью или марковскими сообщениями (источниками).
Как указывается в книге Л.Бриллюэна [с.46], учет в английских словах двухбуквенных сочетаний понижает среднюю информацию на знак до значения I2 (e) =3,32 бит, учет трехбуквенных – до I3 (e) =3,10 бит. Шеннон сумел приблизительно оценить I5 (e)  2,1 бит, I8 (e)
2,1 бит, I8 (e)  1,9 бит. Аналогичные исследования для русского языка дают: I2 (r) = 3,52 бит; I3 (r) = 3,01 бит.
1,9 бит. Аналогичные исследования для русского языка дают: I2 (r) = 3,52 бит; I3 (r) = 3,01 бит.
Последовательность I, I1, I2. является убывающей в любом языке. Экстраполируя ее на учет бесконечного числа корреляций, можно оценить предельную информацию на знак в данном языке 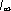 , которая будет отражать минимальную неопределенность, связанную с выбором знака алфавита без учета семантических особенностей языка, в то время как I является другим предельным случаем, поскольку характеризует наибольшую информацию, которая может содержаться в знаке данного алфавита. Шеннон ввел величину, которую назвал относительной избыточностью языка :
, которая будет отражать минимальную неопределенность, связанную с выбором знака алфавита без учета семантических особенностей языка, в то время как I является другим предельным случаем, поскольку характеризует наибольшую информацию, которая может содержаться в знаке данного алфавита. Шеннон ввел величину, которую назвал относительной избыточностью языка :
Избыточность является мерой бесполезно совершаемых альтернативных выборов при чтении текста. Эта величина показывает, какую долю лишней информации содержат тексты данного языка; лишней в том отношении, что она определяется структурой самого языка и, следовательно, может быть восстановлена без явного указания в буквенном виде.
Исследования Шеннона для английского языка дали значение 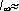 1,4÷1,5 бит, что по отношению к I=4,755 бит создает избыточность около 0,68. Подобные оценки показывают, что и для других европейских языков, в том числе русского, избыточность составляет 60 – 70%. Это означает, что в принципе возможно почти трехкратное (!) сокращение текстов без ущерба для их содержательной стороны и выразительности. Например, телеграфные тексты делаются короче за счет отбрасывания союзов и предлогов без ущерба для смысла; в них же используются однозначно интерпретируемые сокращения "ЗПТ" и "ТЧК" вместо полных слов (эти сокращения приходится использовать, поскольку знаки "." и "," не входят в телеграфный алфавит). Однако такое "экономичное" представление слов снижает разборчивость языка, уменьшает возможность понимания речи при наличии шума (а это одна из проблем передачи информации по реальным линиям связи), а также исключает возможность локализации и исправления ошибки (написания или передачи) при ее возникновении. Именно избыточность языка позволяет легко восстановить текст, даже если он содержит большое число ошибок или неполон (например, при отгадывании кроссвордов или при игре в "Поле чудес"). В этом смысле избыточность есть определенная страховка и гарантия разборчивости.
1,4÷1,5 бит, что по отношению к I=4,755 бит создает избыточность около 0,68. Подобные оценки показывают, что и для других европейских языков, в том числе русского, избыточность составляет 60 – 70%. Это означает, что в принципе возможно почти трехкратное (!) сокращение текстов без ущерба для их содержательной стороны и выразительности. Например, телеграфные тексты делаются короче за счет отбрасывания союзов и предлогов без ущерба для смысла; в них же используются однозначно интерпретируемые сокращения "ЗПТ" и "ТЧК" вместо полных слов (эти сокращения приходится использовать, поскольку знаки "." и "," не входят в телеграфный алфавит). Однако такое "экономичное" представление слов снижает разборчивость языка, уменьшает возможность понимания речи при наличии шума (а это одна из проблем передачи информации по реальным линиям связи), а также исключает возможность локализации и исправления ошибки (написания или передачи) при ее возникновении. Именно избыточность языка позволяет легко восстановить текст, даже если он содержит большое число ошибок или неполон (например, при отгадывании кроссвордов или при игре в "Поле чудес"). В этом смысле избыточность есть определенная страховка и гарантия разборчивости.
На практике учет корреляций в сочетаниях знаков сообщения весьма затруднителен, поскольку требует объемных статистических исследований текстов. Кроме того, корреляционные вероятности зависят от характера текстов и целого ряда иных их особенностей. По этим причинам в дальнейшем мы ограничим себя рассмотрением только шенноновских сообщений, т.е. будем учитывать различную (априорную) вероятность появления знаков в тексте, но не их корреляции.
Со следующего шага мы начнем рассматривать теорию кодирования .

