Связь координат вектора в разных базисах

Пусть L – линейное пространство над полем Р и пусть в нём зафиксированы два базиса е = (е₁, е₂,… , е_n ) и е 1 = (е₁ 1 , е₂ 1 ,… , е_n 1 ). Пусть

(23)

Если ввести матрицу Т = ,

то систему (23) можно записать в матричном виде е 1 = е×Т (24).

Матрица Т называется матрицей перехода от базиса е к базису е 1 . Так как векторы е₁ 1 , е₂ 1 ,… , е_n 1 линейно независимы, то матрица Т невырожденная.

Если вектор а в базисе е имеет координаты х = (a₁, a₂, … , a_n) Т , а в базисе е 1 его координаты х 1 = (b₁, b₂,…, b_n) Т , то а = е×х и а = е 1 ×х 1 . отсюда е×х = е 1 ×х 1 . Используя формулу (24), получим е×х = (е×Т)×х 1 = е× (Т×х 1 ). Отсюда х = Т×х 1 (25). Формула (25) даёт связь координат одного и того же вектора в разных базисах. Её называют формулой преобразования координат.

Пример. Пусть е = (е₁, е₂, е₃ , е₄ ) – базис в пространстве L₄. Пусть е₁ 1 = 2е₁ – 3е₃ , е₂ 1 = е₂ + е₄ , е₃ 1 = 4е₁ + е₂ – е₄ , е₄ 1 = е₂ + 3е₃ – е₄ ; е₁ 11 = е₁ + е₂ , е₂ 11 = е₁ – е₃ , е₃ 11 = е₃ + е₄ , е₄ 11 = е₃ – е₄ . Покажите, что е 1 = (е₁ 1 , е₂ 1 ,… , е_n 1 ) и е 11 = (е₁ 11 , е₂ 11 ,… , е_n 11 )являются базисами в L.. Вектор а в базисе е 1 имеет координаты (1, 4, –2, 5). Найдите координаты этого вектора в базисе е 11 .

Решение. Составим определители матриц перехода Т₁и Т₂ от базиса е к е 1 и е 11 соответственно.

|Т1|= ,

|Т2| = ,

|Т1|= =–12

|Т₂| = = 2. Так как матрицы Т₁ иТ₂ невырожденные, то е 1 и е 11 – базисы.

Найдём Т₂ -1 . Для этого вычислим все алгебраические дополнения элементов матрицы Т₂.

А₁₁= 0, А₁₂ = – = 1, А₁₃ = = 1, А₁₄ = – = 1, А₂₁ = – , А₂₂ = = –2, А₂₃ = – = –1, А₂₄ = = –1, А₃₁ = = 0, А₃₂ = – = 0, А₃₃ = = 1, А₃₄ = – = –1, А₄₁ = – = 0, А₄₂ = 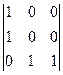= 0. А₄₃ = – = 1, А₄₄ = = –1. Используя найденные алгебраические дополнения, получим Т₂ -1 = . Следовательно, = = . Итак, в базисе е 11 данный вектор имеет координаты ( –10; 0; –17).

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

Утверждения теоремы в наших обозначениях выглядят следующим образом:

Это означает, что скобки б · , · с обладают свойством линейности по второму аргументу.

2.Матрица перехода от одного базиса к другому. Связь координат вектора в разных базисах.

:Xn → Xn — линейный оператор. Зададим в Xn два базиса: "старый" базис e = (e1, e2, … , en) и "новый" базис f = (f1, f2, … , fn) .

index_entry("000") Матрицей перехода от базиса e к базису f называется матрица C = (cik) (i,k = 1, … ,n) , столбцами которой являются координатные столбцы векторов f1, f2, … ,fn в базисе e , т. е.

или в матричной форме:

где C — матрица перехода

Замечание. В силу линейной независимости базисных векторов матрица C — невырожденная ( det C ≠ 0 ). Следовательно, C имеет обратную матрицу C − 1 .

Теорема 1. Преобразование координат вектора при переходе от "старого" базиса e к "новому" базису f определяется формулой:

Доказательство. Обозначим координатные столбцы произвольного вектора
x О Xn в "старом" базисе e и в "новом" базисе f

Произвольный вектор x в базисе e имеет вид:

В базисе f тот же вектор имеет вид:

и в силу формулы (1)

Сравнивая формулы (3) и (4), получаем

Умножая это равенство слева на C −1 , получаем формулу (2), которую требовалось доказать.

Пусть линейный оператор

: Xn → Xn в базисе e имеет матрицу Ae . Найдем матрицу этого оператора Af в базисе f . Пусть C — матрица перехода от базиса e к базису f .

Теорема. index_entry("000") Преобразование матрицы оператора

при переходе от "старого" базиса e к "новому" базису f определяется формулой:

Рассмотрим произвольный вектор x и его образ y =

x . Обозначим координатные столбцы этих векторов: Xe и Ye — в "старом" базисе e ; Xf и Yf — в "новом" базисе f .

Отсюда, используя формулы преобразования вектора, получаем

Сравнивая с выражением Yf = Af · Xf , приходим к формуле (1), которую требовалось доказать.

3.Подпространства линейного пространства. Теорема о размерностях суммы и пересечения подпространств.

Подпространство линейного пространства

Множество называется подпространством линейного пространства V, если:

1)

2)

Определение. Пусть – линейные подпространства в L. Их суммой называется множество

Легко убедиться, что сумма также является линейным подпространством и что эта операция сложения ассоциативна и коммутативна, так же как и операция пересечения линейных подпространств. Другое описание суммы L1 + . + Ln состоит в том, что это наименьшее подпространство в L, содержащее все Li.

Следующая теорема связывает размерности суммы двух подпространств и их пересечения:

3. Теорема. Если конечномерны, то и L1 + L2 конечномерны и

dim() + dim(L1 + L2) = dim L1 + dim L2.

Доказательство. L1 + L2 является линейной оболочкой объединения базисов L1 и L2 и потому конечномерно; содержится в конечномерных пространствах L1 и L2.Положим m = dim , n = dim L1, p = dim L2. Выберем базис <e1, . em> пространства , его можно дополнить до базисов пространств L1 и L2: пусть это будет и . Назовем такую пару базисов в L1 и L2 согласованной.

Пусть в линейном пространстве Х_п заданы базисы Разложим векторы базиса е’ по базису е:

называют матрицей перехода от базиса е к базису е’. Заметим, что столбцами матрицы Т являются столбцы координат соответствующих векторов базиса е! в базисе е.

Соотношения (4.15) устанавливают связь между базисами е и е’. Эти соотношения удобно записать в матричной форме

Точно так же векторы базиса е можно разложить по базису е’, и тогда придем к соотношению

где Т’ — матрица перехода от базиса е’ к базису е. Столбцами матрицы Т’ служат координатные столбцы соответствующих векторов базиса е в базисе е‘.

Из соотношений е = е’ Т’ и е’ = е Т следуют выражения

из которых вытекают соотношения

Из этих соотношений в силу линейной независимости векторов базисов еие’ получаем: ТТ’ = Т’ Т = Е. Следовательно, Т’ = Т

Таким образом, матрица перехода от одного базиса п-мерного линейного пространства к другому является невырожденной матрицей n-го порядка с элементами из основного поля Р. Верно и противоположное утверждение, т.е. верна следующая теорема.

Теорема ^.10. Любая невырожденная квадратная матрица п-го порядка с элементами из поля Р служит матрицей перехода от данного базиса п-мерного линейного пространства X над полем Р к некоторому другому базису в X.

> Пусть даны базис е = (ei,e2, . е_п) линейного пространства X и невырожденная квадратная матрица

n-го порядка с элементами из поля Р. В пространстве X выберем упорядоченную систему векторов е’ = (е[, е’₂,е’_п), для которых столбцы матрицы Т являются координатными столбцами в базисе е.

Система векторов е’ состоит из п векторов и является линейно независимой, так как у невырожденной матрицы Т столбцы линейно независимы. Поэтому эта система — базис в линейном пространстве X, причем в силу выбора векторов системы выполняется равенство е’ = еТ. Это означает, что матрица Т представляет собой матрицу перехода от базиса е к базису е!. ?

Из доказанной теоремы вытекает, что в n-мерном лиейном пространстве X над полем Р существует столько различных базисов, сколько существует различных невырожденных квадратных матриц n-го порядка с элементами из поля Р. При этом учтено, что различны базисы, состоящие из одних векторов, но по-разному упорядоченных.

Практическое правило. Для построения матрицы Т перехода от базиса е к базису е! нужно для каждого вектора е’ базиса е! найти координаты в базисе е и из них, как из столбцов, построить матрицу Т.

Если векторы базисов е и е! заданы координатами в некотором базисе е°, то для отыскания координат вектора е’ в базисе е следует составить векторное равенство

от него перейти к покоординатным равенствам и из полученной системы уравнений найти искомый столбец координат (ац, «2, . а_п) Т вектора е’ в базисе е.

При отыскании матрицы Т можно также пользоваться формулой

где Т — матрица перехода от базиса е° к базису е, Т — матрица перехода от базиса е° к базису е!.

Чтобы доказать формулу (4.19), замечаем, что выполняются соотношения

Из этих соотношений получаем: е’ = е° Т2 = (еТ₁ _1 )Т2 = е(Т₁ _1 Т2), откуда следует, что Т^ 1 Т2 — матрица перехода от базиса е к базису е!, т.е. верно равенство (4.19).

Пример 4.9. Найти матрицу перехода от базиса е = (ei,62) к базису е’ = (ефе^), где [е[]_е = (2,1) т , [е’₂]_е = (3,2) т .

Решение. Здесь векторы нового базиса заданы координатами в старом базисе. Поэтому сразу можно составить искомую матрицу Т из координатных столбцов векторов е[ и е’₂:

Пример 4.10. Найти матрицу’ перехода от базиса е = (ei,62, ез) к базису е’ = (еф е’₂,е’₃), где векторы заданы своими координатами в некотором базисе: е = (1,1,1) т , 62 = (1,2,3) т , ез = (1,0,1) т , е = (-1,0,1) т , е’₂ = (1,3, 3) т , е’₃ = (1,-1,-1) т .

Решение. Составим векторное равенство

При j = 1 это равенство принимает вид:

Это равенство приводит к системе

из которой находим: а. = —2, од = 1, аз = 0. Следовательно, е[ = —2 е +б2- Аналогично при j = 2 и j = 3 получаем е(> = 61+62 — 63,63 = ei — 62 + ез. Из коэффициентов полученных разложений записываем матрицу перехода

Можно также этот ответ получить по формуле (4.19). Дли этого, пользуясь координатами векторов, записываем матрицы перехода

Пример 4.11. В линейном пространстве Р^х] многочленов не выше второй степени с действительными коэффициентами даны два базиса: е = (е!,е2,ез), где е = 1, ег = х, ез = х 2 , и е’ = (e’_l5 е’₂, е’₃), где е[ = 1, е’₂ — х — 1, е’₃ — (х — I) 2 . Найти матрицу перехода Т от базиса е к базису е’.