Содержание
1. Машинные коды
4. Дополнительный код
5. Модифицированные обратные и дополнительные коды
6. Арифметические действия в машинных кодах.
Для выполнения арифметических операций используют специальные коды представления чисел, которые позволяют свести операцию вычитания чисел к арифметическому сложению этих кодов. Различают прямой код (П), обратный код (ОК) и дополнительныйкод (ДК). Прямой код используется для представления отрицательных чисел в памяти компьютера, а также при выполнении операций умножения и деления. Обратный и дополнительный коды применяются для выполнения операции вычитания, которую заменяют операцией сложения чисел с разными знаками: а – b = а + (-b).
Прямой код целого числа. Под прямым кодом двоичного числа понимают запись самого числа. Значение знакового разряда для положительных чисел определяют равным нулю (0), для отрицательных чисел — единице (1). Например, если для записи кода используется байт, то [1] :
| Число | Прямой код |
| +1101 | 0,0001101 |
| -1101 | 1,0001101 |
Крайний левый разряд в прямом коде нами отведен под знак числа, остальные разряды — под само число. Число располагаем в разрядной сетке так, чтобы цифра младшего разряда числа занимала крайнюю правую ячейку.
Знаковый разряд —> | 0, | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
Обратный код целого положительного числа совпадает с его прямым кодом. Для отрицательного числа обратный код строится заменой каждого незнакового байта его представления в прямом коде на противоположный (заменим 1 на 0, 0 на 1), знаковый разряд не изменяется.
| Число | Прямой код | Обратный код | Замечание |
| +11011 | 0,0011011 | 0,0011011 | Число положительное, обратный и прямой коды совпадают |
| -11011 | 1,0011011 | 1,1100100 | Число отрицательное, каждый байт, кроме знакового, изменен на противоположный |
Наиболее важные свойства обратного кода чисел:
· сложение положительного числа С с его отрицательным значением в обратном коде дает т.н. машинную единицу МЕок=1|11…11, состоящую из единиц в знаковом и в значащих разрядах числа;
· нуль в обратном коде имеет двоякое значение. Он может быть как положительным числом – 0|00…00, так и отрицательным 1|11…11. Значение отрицательного числа совпадает с МЕок. Двойственное представление 0 явилось причиной того, что в современных ЭВМ все числа представляются не обратным, а дополнительным кодом.
Дополнительный код положительного числа совпадает с его прямым кодом. Для отрицательного числа дополнительный код образуется путем получения обратного кода и добавлением к младшему разряду единицы (2 0 – для целых чисел, 2 -л – для дробных).
| Число | Прямой код | Обратный код | Дополнительный код |
| + 1110 | 0,0001110 | 0,0001110 | 0.0001110 |
| -1110 | 1,0001110 | 1,1110001 | 1,1110010 |
Основные свойства дополнительного кода:
· сложение дополнительных кодов положительного числа С с его отрицательным значением дает т.н. машинную единицу дополнительного кода:
МЕдк=МЕок + 2 0 = 10|00…00, т.е. число 10 (два) в знаковых разрядах числа;
· дополнительный код называется так потому, что представление отрицательных чисел является дополнением прямого кода чисел до машинной единицы МЕдк.
Модифицированные обратные и дополнительные коды
Модифицированные обратные и дополнительные коды двоичных чисел отличаются соответственно от обратных и дополнительных кодов удвоением значений знаковых разрядов. В модифицированных обратном и дополнительном кодах под знак числа отводится не один, а два разряда: «00» соответствует знаку «плюс», «11» — знаку «минус». Любая другая комбинация («01» или «10»), получившаяся в знаковых разрядах, является признаком переполнения разрядной сетки. Сложение чисел в модифицированных кодах ничем, не отличается от сложения в обычных обратном и дополнительном кодах.
Значение знаковых разрядов «01» свидетельствует о положительном переполнении разрядной сетки, а «10» – об отрицательном переполнении. В настоящее время практически во всех компьютерах роль сдвоенных разрядов для фиксации переполнения разрядной сетки играют переносы, идущие в знаковый и из знакового разряда.
Сложение и вычитание чисел со знаком в дополнительном коде
Если оба числа имеют n–разрядное представление, то алгебраическая сумма будет получена по правилам двоичного сложения (включая знаковый разряд), если отбросить возможный перенос из старшего разряда. Если числа принадлежат диапазону представимых данных и имеют разные знаки, то сумма всегда будет лежать в этом диапазоне. Переполнение может иметь место, если оба cлагаемых имеют одинаковые знаки.
Пример 1:
6 – 4 = ?
6 – положительное число с кодом 0110
–4 – отрицательное число с дополнительным кодом 1100
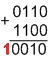 (перенос игнорируется): 6 – 4 = 2.
(перенос игнорируется): 6 – 4 = 2.
–5 + 2 = ?
2 – положительное число с кодом 0010
–5 – отрицательное число с дополнительным кодом 1011
 Число с кодом 1101 является отрицательным, модуль этого числа имеет код 00112 = 310.
Число с кодом 1101 является отрицательным, модуль этого числа имеет код 00112 = 310.
Арифметические действия в машинных кодах.
Сложение (вычитание). Операция вычитания приводится к операции сложения путем преобразования чисел в обратный или дополнительный код согласно таблице.
| Требуемая операция | Необходимое преобразование |
| А+В | А+В |
| А-В | А+(-В) |
| -А+В | (-А)+В |
| -А-В | (-А)+(-В) |
Здесь А и В неотрицательные числа. Скобки в представленных выражениях указывают на замену операции вычитания операцией сложения с обратным или дополнительным кодом соответствующего числа. Сложение двоичных чисел осуществляется последовательно, поразрядно в соответствии с таблицей. При выполнении сложения цифр необходимо соблюдать следующие правила:
1. Слагаемые должны иметь одинаковое число разрядов. Для выравнивания разрядной сетки слагаемых можно дописывать незначащие нули слева к целой части числа и незначащие нули справа к дробной части числа.
2. Знаковые разряды участвуют в сложении так же, как и значащие.
3. Необходимые преобразования кодов производятся с изменением знаков чисел. Приписанные незначащие нули изменяют свое значение при преобразованиях по общему правилу.
4. При преобразовании единицы переноса из старшего знакового разряда, в случае использования ОК, эта единица складывается с младшим числовым разрядом. При использовании ДК единица переноса теряется. Знак результата формируется автоматически, результат представляется в том коде, в котором представлены исходные слагаемые.
Пример 1. Сложить два числа: А10 = 7, В10 = 16.
Исходные числа имеют различную разрядность, необходимо провести выравнивание разрядной сетки:
Сложение в обратном или дополнительном коде дает один и тот же результат:
Пример 2. Сложить два числа: А10 = +16, В10 = -7 в ОК и ДК.
По таблице необходимо преобразование А+(-В), в которой второй член преобразуется с учетом знака

При сложении чисел в ОК и ДК были получены переносы в знаковый разряд и из знакового разряда. В случае ОК перенос из знакового разряда требует дополнительного прибавления единицы младшего разряда (п.4 правил). В случае ДК этот перенос игнорируется.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Учись учиться, не учась! 10623 –  | 8001 –
| 8001 –  или читать все.
или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
При выполнении арифметических операций в современных ЭВМ используется представление положительных чисел в прямом коде (ПК), а отрицательных – в обратном (ОК) или в дополнительном (ДК) кодах. Это можно проиллюстрировать схемой на рис. 2.4.
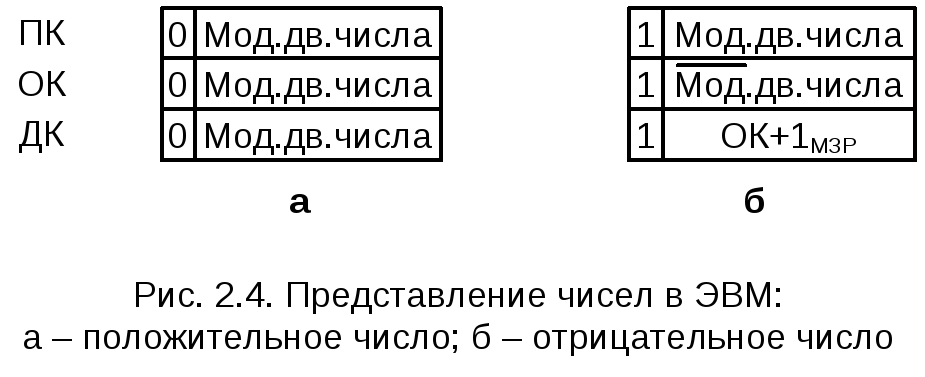
Общее правило. При алгебраическом сложении двух двоичных чисел, представленных обратным (или дополнительным) кодом, производится арифметическое суммирование этих кодов, включая разряды знаков. При возникновении переноса из разряда знака единица переноса прибавляется к МЗР суммы кодов при использовании ОК и отбрасывается при использовании ДК. В результате получается алгебраическая сумма в обратном (или дополнительном) коде.
Рассмотрим подробнее алгебраическое сложение для случая представления отрицательных чисел в ДК.
При алгебраическом сложении чисел со знаком результатом также является число со знаком. Суммирование происходит по всем разрядам, включая знаковые, которые при этом рассматриваются как старшие. При переносе из старшего разряда единица переноса отбрасывается и возможны два варианта результата:
знаковый разряд равен нулю: результат – положительное число в ПК;
знаковый разряд равен единице: результат – отрицательное число в ДК.
Для определения абсолютного значения результата его необходимо инвертировать, затем прибавить единицу.
Вычислить алгебраическую сумму 58-23.

Вычислить алгебраическую сумму 26-34.


Вычислить алгебраическую сумму -5-1.

4.1.Какие Вы знаете позиционные системы счисления?
4.2.Сформулируйте правила перевода целых чисел из десятичной системы счисления в двоичную, восьмеричную, шестнадцатеричную;
4.3.Сформулируйте правила перевода целых чисел из двоичной системы счисления в восьмеричную, шестнадцатеричную и обратно;
4.4.Сформулируйте правила перевода вещественных (дробных и смешанных) чисел из десятичной системы счисления в двоичную;
4.5. Сформулируйте правила выполнения арифметических действий
4.6. Сформулируйте правила построения обратного кода
4.7. Сформулируйте правила построения дополнительного кода кода
1. Таблица 1.1 – Варианты заданий к лабораторной работе № 1
Исходное целое десятичное число
Исходное вещественное десятичное число
Указанные числа представить в двоичной ,восьмиричной и шестнадцетиричной системах
Популярное
- Устройство и программирование микроконтроллеров AVR для начинающих – 143
- Трехканальный термостат, терморегулятор, таймер на ATmega8 – 70
- Двухканальный термостат, терморегулятор на ATmega8 – 67
Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа
Прямой, обратный и дополнительный коды двоичного числа — способы представления двоичных чисел с фиксированной запятой в компьютерной (микроконтроллерной) арифметике, предназначенные для записи отрицательных и неотрицательных чисел

Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.
Прямой код
Прямой код — способ представления двоичных чисел с фиксированной запятой. Главным образом используется для записи неотрицательных чисел
Прямой код используется в двух вариантах.
В первом (основной) — для записи только неотрицательных чисел:
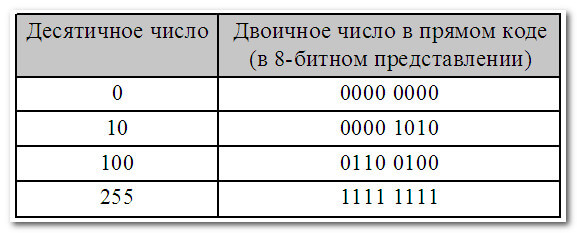 В этом варианте (для восьмибитного двоичного числа) мы можем записать максимальное число 255 (всего чисел 256 — от 0 до 255)
В этом варианте (для восьмибитного двоичного числа) мы можем записать максимальное число 255 (всего чисел 256 — от 0 до 255)
Второй вариант — для записи как положительных, так и отрицательных чисел.
В этом случае старший бит (в нашем случае — восьмой) объявляется знаковым разрядом (знаковым битом).
При этом, если:
— знаковый разряд равен 0, то число положительное
— знаковый разряд равен 1, то число отрицательное

В этом случае диапазон десятичных чисел, которые можно записать в прямом коде составляет от — 127 до +127:
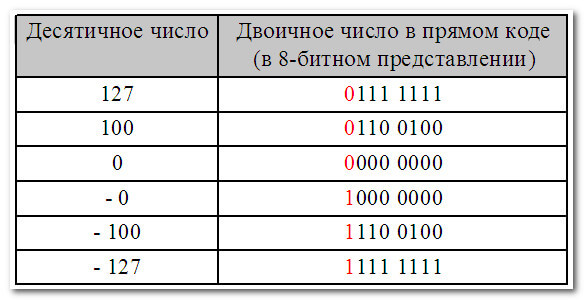 Подводя итоги вопроса, не влезая в его дебри, скажу одно:
Подводя итоги вопроса, не влезая в его дебри, скажу одно:
Прямой код используется главным образом для представления неотрицательных чисел.
Использование прямого кода для представления отрицательных чисел является неэффективным — очень сложно реализовать арифметические операции и, кроме того, в прямом коде два представления нуля — положительный ноль и отрицательный ноль (чего не бывает):
Обратный код
Обратный код — метод вычислительной математики, позволяющий вычесть одно число из другого, используя только операцию сложения.
Обратный двоичный код положительного числа состоит из одноразрядного кода знака (битового знака) — двоичной цифры 0, за которым следует значение числа.
Обратный двоичный код отрицательного числа состоит из одноразрядного кода знака (битового знака) — двоичной цифры 1, за которым следует инвертированное значение положительного числа.
Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.
При 8-битном двоичном числе — знаковый бит (как и в прямом коде) старший (8-й)

Диапазон десятичных чисел, который можно записать в обратном коде от -127 до + 127
Арифметические операции с отрицательными числами в обратном коде:
1-й пример (для положительного результата)
Дано два числа:
100 = 0110 0100
-25 = — 0001 1001
Необходимо их сложить:
100 + (-25) = 100 — 25 = 75
1-й этап
Переводим число -25 в двоичное число в обратном коде:
25 = 0 001 1001
-25= 1 110 0110
и складываем два числа:
0 110 0100 (100) + 1 110 0110 (-25) = 1 0 100 1010, отбрасываем старшую 1 (у нас получился лишний 9-й разряд — переполнение), = 0 100 1010
2-й этап
Отброшенную в результате старшую единицу прибавляем к результату:
0 100 1010 + 1 = 0 100 1011 (знаковый бит = 0 , значит число положительное), что равно 75 в десятичной системе
2-й пример (для отрицательного результата)
Дано два числа:
5 = 0000 0101
-10 = — 0000 1010
Необходимо их сложить:
5 + (-10) = 5 — 10 = -5
1-й этап
Переводим число -10 в двоичное число в обратном коде:
10 = 0 000 1010
-10= 1 111 0101
и складываем два числа:
0 000 0101 (5) + 1 111 0101 (-10) = 1 111 1010 (знаковый бит = 1 , значит число отрицательное)
2-й этап
Раз результат получился отрицательный, значит число представлено в обратном коде.
Переводим результат в прямой код (путем инвертирования значения, знаковый бит не трогаем):
1 111 1010 —-> 1 000 0101
Проверяем:
1 000 0101 = — 0000 0101 = -5
Обратный код решает проблему сложения и вычитания чисел с различными знаками, но и имеет свои недостатки:
— арифметические операции проводятся в два этапа
— как и в прямом коде два представления нуля — положительный и отрицательный
Дополнительный код
Дополнительный код — наиболее распространенный способ представления отрицательных чисел. Он позволяет заменить операцию вычитания на операцию сложения и сделать операции сложения и вычитания одинаковыми для знаковых и беззнаковых чисел.
В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).
Диапазон десятичных чисел которые можно записать в дополнительном коде от -128 до +127. Запись положительных двоичных чисел в дополнительном коде та-же, что и в прямом и обратном кодах.

Дополнительный код отрицательного числа можно получить двумя способами
1-й способ:
— инвертируем значение отрицательного числа, записанного в прямом коде (знаковый бит не трогаем)
— к полученной инверсии прибавляем 1
Пример:
Дано десятичное число -10
Переводим в прямой код:
10 = 0 000 1010 —-> -10 = 1 000 1010
Инвертируем значение (получаем обратный код):
1 000 1010 —-> 1 111 0101
К полученной инверсии прибавляем 1:
1 111 0101 + 1 = 1 111 0110 — десятичное число -10 в дополнительном коде
2-й способ:
Вычитание числа из нуля
Дано десятичное число 10, необходимо получить отрицательное число (-10) в дополнительном двоичном коде
Переводим 10 в двоичное число:
10 = 0 000 1010
Вычитаем из нуля:
0 — 0000 1010 = 1 111 0110 — десятичное число -10 в дополнительном коде

Арифметические операции с отрицательными числами в дополнительном коде
Дано: необходимо сложить два числа -10 и 5
-10 + 5 = -5
Решение:
5 = 0000 0101
-10 = 1111 0110 (в дополнительном коде)
Складываем:
1111 0110 + 0000 0101 = 1111 1011, что соответствует числу -5 в дополнительном коде
Как мы видим на этом примере — дополнительный код отрицательного двоичного числа наиболее подходит для выполнения арифметических операций сложения и вычитания отрицательных чисел.
Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода




 (27 голосов, оценка: 4,89 из 5)
(27 голосов, оценка: 4,89 из 5)
