Приведённое выше определение плотности множества эквивалентно любому из нижеперечисленных:
- Множество A плотно в B тогда и только тогда, когда замыканиеAсодержитB , то есть
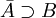 В частности, A всюду плотно, если
В частности, A всюду плотно, если 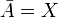 .
. - Множество A плотно в B тогда и только тогда, когда внутренностьдополнения к A не пересекается с B , то есть
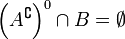 . В частности, A всюду плотно, если
. В частности, A всюду плотно, если 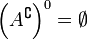 .
.
Примеры
- Любое множество плотно в себе.
- Множество рациональных чисел
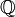 плотно в пространстве вещественных чисел
плотно в пространстве вещественных чисел .
.
См. также
Ссылки
Wikimedia Foundation . 2010 .
Смотреть что такое "Всюду плотное множество" в других словарях:
ВСЮДУ ПЛОТНОЕ МНОЖЕСТВО — Атопологического пространства X множество, определяемое свойством: , где замыкание множества А. Другими словами, в любом открытом в Xмножестве имеется хотя бы одна точка из множества А. Употребляется также термин плотное множество . А. А. Мальцев … Математическая энциклопедия
ПЛОТНОЕ МНОЖЕСТВО — то же, что всюду плотное множество. Более общо, множество Аназ. плотным в открытом множестве Gпространства X, если G содержится в замыкании Аили, что то же самое, если всюду плотно в подпространстве . Если Ане плотно ни в каком непустом открытом… … Математическая энциклопедия
Плотное множество — подмножество пространства, точками которого можно сколь угодно хорошо приблизить любую точку объемлющего пространства. Формально говоря, A плотно в X, если всякая окрестность любой точки x из X содержит элемент A. Содержание 1 Определения 2… … Википедия
Нигде не плотное множество — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Множество второй категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Множество первой категории — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Массивное множество — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Несвязное множество — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
Связное множество — Курсив обозначает ссылку на этот словарь # А Б В Г Д Е Ё Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш … Википедия
ВПОЛНЕ НЕПРИВОДИМОЕ МНОЖЕСТВО — множество Млинейных операторов в локально выпуклом топологическом векторном пространстве Е, всюду плотное в алгебре S(E).всех слабо непрерывных линейных операторов в Е;при этом S(E).рассматривается в слабой операторной топологии. Понятие В. н. м … Математическая энциклопедия





1.4.7. Плотность и сепарабельность
Определение 1. Множество M называется плотным в множестве N, если N⊂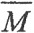 , то есть любой элемент из множества N есть предельная точка множества M.
, то есть любой элемент из множества N есть предельная точка множества M.
Определение 2. Если множество N = X, то есть совпадает со всем носителем метрического пространства X, то множество M называется всюду плотным в множестве X.
( Комментарий. Всюду плотность означает, что любой элемент из множества X есть предел последовательности элементов из множества M, то есть ∀x ∈X в любой, сколь угодно малой окрестности точки найдутся точки из множества M, то есть все точки x ∈X есть точки прикосновения множества M, то есть замыкание множества M совпадает со всем пространством.)
Определение 3. Пусть M – произвольное множество метрического пространства (X,ρ). Множество M называется нигде не плотным в множестве X, если замыкание множества M не содержит ни одного непустого шара множества X, то есть в каждом открытом шаре B⊂X найдётся шар B’⊂B, не содержащий точек из множества M.
- Множество рациональных чисел всюду плотно на действительной оси, то есть любое действительное число является либо рациональным числом, либо пределом последовательности рациональных чисел.
- Множество целых чисел Z нигде не плотно на действительной оси X, так как замыкание множества Z совпадает самим множеством Z и оно не содержит ни одного непустого шара множества X.
- В пространстве C[a,b] плотны линейные многообразия тригонометрических и алгебраических полиномов.
- Любая изолированная точка в любом пространстве есть нигде не плотное множество.
- Любое подмножество нигде не плотного множества нигде не плотно.
- Объединение конечного числа нигде не плотных множеств нигде не плотно.
- Объединение счётного числа нигде не плотных множеств уже не нигде не плотно. Оно может быть даже всюду плотно. Множество рациональных чисел счётное всюду плотное множество на действительной оси, но оно есть объединение счётного числа изолированных точек.
Определение 4. Метрическое пространство (X,ρ) сепарабельно, если в нём существует счётное всюду плотное множество "счётный скелет".
( Комментарий. Сепарабельность означает, что в пространстве (X,ρ) существует последовательность n>, такая, что ∀x ∈X из неё можно выделить (separate (лат) – выделять) подпоследовательность nk>, сходящуюся к элементу х, или, что то же самое, ∃n>∈X:(∀ε>0)^(∀x ∈X)∃xnk∈n>: ρ(x,xnk) n 2 сепарабельно. Счётный скелет в нём – множество точек с рациональными координатами.
- Дискретное метрическое пространство, состоящее из счётного числа точек, сепарабельно, потому, что, по определению, множество называется всюду плотным, если его замыкание совпадает со всем пространством. Здесь счётный скелет совпадает со всем пространством, а других точек нет.
- Пространство C[a,b] сепарабельно, так как счётный скелет здесь образует множество полиномов с рациональными коэффициентами, а по теореме Вейерштрасса любую функцию из C[a,b] можно сколь угодно точно приблизить суммой таких полиномов.
- Пространство l2 сепарабельно.
 Рассмотрим множество L всех последовательностей с рациональными членами, у которых только конечное, для каждого своё, число членов не равно нулю, а остальные члены нулевые. Это множество счётно, как объединение счётного числа счётных множеств. Покажем, что множество L образует счётный скелет в l2. Пусть последовательность n>∈l2. Так как
Рассмотрим множество L всех последовательностей с рациональными членами, у которых только конечное, для каждого своё, число членов не равно нулю, а остальные члены нулевые. Это множество счётно, как объединение счётного числа счётных множеств. Покажем, что множество L образует счётный скелет в l2. Пусть последовательность n>∈l2. Так как 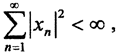 то есть ряд сходится, то
то есть ряд сходится, то 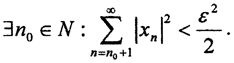 Так как множество рациональных чисел Q всюду плотно на числовой оси, то
Так как множество рациональных чисел Q всюду плотно на числовой оси, то 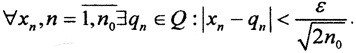 Нормировочный множитель выбран для удобства и в силу произвольности ε. Рассмотрим последовательность n>∈L, члены которой при n>n+1 равны нулю. Тогда расстояние между x∈l2 и q∈Q
Нормировочный множитель выбран для удобства и в силу произвольности ε. Рассмотрим последовательность n>∈L, члены которой при n>n+1 равны нулю. Тогда расстояние между x∈l2 и q∈Q 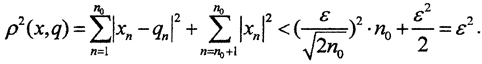 Это значит, что ρ(x,q)
Это значит, что ρ(x,q)
Топологическое пространство (X,Ω) называется сепарабельным, если X содержит не более чем счетное подмножество А, замыкание которого совпадает с X. Таким образом, сепарабельные пространства – это пространства, которые содержат не более чем счетные всюду плотные множества. Эти пространства имеют ряд полезных свойств и играют важную роль во многих разделах математики.
- Числовая прямая R 1 со стандартной топологией является сепарабельным пространством, поскольку содержит счетное всюду плотное множество Q рациональных точек.
- Дискретное топологическое пространство, состоящее из несчетного множества точек , является простым примером несепарабельного топологического пространства.
- Всякое топологическое пространство с тривиальной топологией является сепарабельным.
Говорят, что топология Ω обладает счетной базой β, если β состоит не более чем из счетного числа множеств.
Теорема 2.10. Если пространство (X,Ω) обладает счетной базой, то оно сепарабельно.
Доказательство. Пусть β = – некоторая счетная база в X, где индекс i пробегает не более чем счетное множество индексов I. Построим множество А = , выбрав по одной точке ai, из Vi, и докажем, что = X. Так как в силу теоремы 1.6 = А А’, то достаточно показать, что любая точка х множества ХА является предельной точкой множества А. Рассмотрим произвольную окрестность U точки х. Из теоремы 2.4 следует, что найдется такое множество Vi0 β, что х Vi0 U. Так как пересечение Vi0 А , то существует точка ai0 (Vi0 А) U, причем, x аi0. То есть любая окрестность U точки х ХА содержит некоторую точку аi0 А. Это означает, что точка х является предельной точкой множества А: х А’. Следовательно, = А (XА) = X. Таким образом, А является не более чем счетным всюду плотным в X множеством, что и доказывает сепарабельность пространства (X,Ω).
