Поскольку БПФ по сравнению с обычным анализом Фурье многократно уменьшает объём вычислений (см. выше), именно метод БПФ реализован в MS EXCEL инструментом «Анализ Фурье» (рис. 8.9).
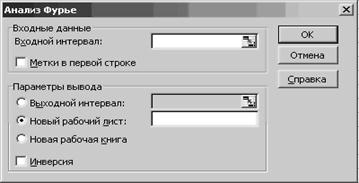
Рис. 8.9. Окно инструмента «Анализ Фурье»
Эта процедура поддерживает также обратные преобразования, при этом инвертирование преобразованных данных возвращает исходные данные. Если установлен флажок в поле «Инверсия», то данные во входном диапазоне считаются преобразованными, и выполняется обратное преобразование, возвращающее их в выходной диапазон в исходном состоянии. Если флажок снят, то выполняется прямое преобразование.
Комплексные данные должны задаваться в формате х + yi. Число значений во входном интервале должно быть равно 2 k (см. выше). Если х является отрицательным числом, перед ним ставится апостроф (‘). Максимальное число значений, предназначенных для БПФ в программе EXCEL, равно 4096.
Пример. Имеются исходные данные, представляющие собой результаты последовательных замеров толщины пластин (см. выше), заданные столбцами в файле «временные ряды». С помощью инструмента «Анализ Фурье» провести прямое и обратное преобразования, построить амплитудный и фазовый спектр.
Алгоритм действий следующий:
1. Формируем таблицу исходных данных:
Сервис – Анализ данных – Анализ Фурье – OK.
Задаём входной интервал в виде столбца данных длиной 2 k , например А10:А137 и выходной интервал (верхнее поле, начиная с которого будут приведены выходные данные) и нажимаем ОК.
Excel представит результаты прямого преобразования Фурье в виде столбца комплексных чисел в формате х + yi.
2. Для восстановления исходных данных после преобразования Фурье за входной интервал необходимо взять столбец результатов прямого преобразования Фурье и поставить флажок в поле «Инверсия».
3. Для построения значений амплитудного спектра воспользуемся функцией или формулой = MHИM.ABS. Сосчитаем с её помощью модуль комплексного числа, расположенного в верхней ячейке столбца комплексных чисел, полученных по п. 1. Затем, копируя ячейки, распространим эту формулу на весь столбец комплексных чисел. По полученному ряду (или столбцу) модулей комплексных чисел можно построить график амплитудного спектра, например, в виде столбчатой диаграммы («Мастер диаграмм» – «Линейчатая»).
4. Для построения значений фазового спектра воспользуемся функцией или формулой = МНИМ.АРГУМЕНТ, выражающей угол наклона вектора комплексного числа в радианах. Аналогично п. 3 распространим эту формулу на весь столбец результатов прямого преобразования Фурье (см. п. 1). По полученным данным аналогично п. 3 можно построить график амплитудного спектра.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Студент – человек, постоянно откладывающий неизбежность. 10809 –  | 7380 –
| 7380 –  или читать все.
или читать все.
Сегодня мы будем тестировать разложение функции в ряд Фурье, которое мы делали на прошлом уроке. И так, напомню, что мы раскладывали в ряд Фурье вот такую функцию:
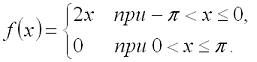
В итоге мы вывели формулу разложения в ряд Фурье для этой функции:
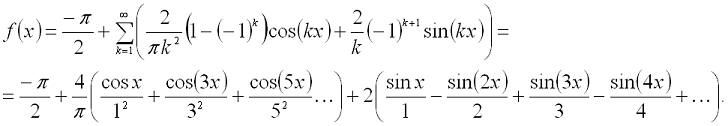
Теперь начинаем ее проверять. И так, открываем Excel и заносим первое значение x (- π) * :

Затем вычисляем остальные значения. Пусть у нас будет шаг π/10*:

Копируем формулы вниз*:

Во втором столбце вычисляем значения функции*:

Поскольку у нас функция выражена зависимостью:
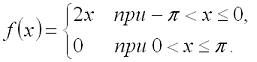
то формулу копируем только до x=0 * :

а дальше заполняем нулями*:

где нибудь в отдельном столбце считаем первый член ряда Фурье, аналогичным образом копируем формулу. Строим еще несколько столбцов с вычислением членов ряда Фурье. Затем суммируем их и строим график*:

Как видим, каждая новая итерация приближает график функции к исходному. Но что бы приближения было идеальным, нам потребуется очень много итераций, поэтому на следующем уроке будем писать программу на C#, которая сделает все расчеты за нас (вплоть до 1000 итераций).
Скриншоты, помеченные знаком *, являются цитатами и иллюстрациями программного продукта " Excel ", авторское право на который принадлежит Microsoft .
Для того, чтобы оценить ресурс, необходимо авторизоваться.
Методическое пособие разработано на кафедре информатики МичГАУ и рекомендовано студентам, изучающим математику, преподавателям, а также аспирантам, сталкивающимся с необходимостью математической обработки данных. В пособии рассмотрены элементы математического анализа, теория вероятностей, математической статистики и приведены примеры решения задач в среде Microsoft Excel.
