Существуют два основных способа задания множеств: перечисление и описание его элементов. Перечисление состоит в получении полного списка элементов множества, а описание заключается в задании такого свойства, которым элементы данного множества обладают, а все остальные нет.
4. Пересечением двух множеств называют множество, состоящее из всех общих элементов этих множеств.
Пример:
Возьмем числа 12 и 18. Найдем их делители, обозначив все множество этих делителей соответственно буквами А и B:
А = <1, 2, 3, 4, 6, 12>,
B = <1, 2, 3, 6, 9, 18>.
Мы видим, что у чисел 12 и 18 есть общие делители: 1, 2, 3, 6. Обозначим их буквой C:
C = <1, 2, 3, 6>.
Множество C и является пересечением множеств А и B. Пишут это так:
А ∩B =C.
Если два множества не имеют общих элементов, то пересечением этих множеств является пустоемножество.
Пустое множество обозначают знаком Ø, а используют такую запись:
X ∩Y = Ø.
Объединение двух множеств – это множество, состоящее из всех элементов этих множеств.
Для примера вернемся к числам 12 и 18 и множеству их элементов A и B. Выпишем сначала элементы множества А, затем добавим к ним те элементы множества B, которых нет во множестве А. Мы получим множество элементов, которым обладают А и B в совокупности. Обозначим его буквой D:
Множество D и является объединением множеств A и B. Пишется это так:
D =AUB.
AUB=<1, 2, 3, 4, 6, 12, 9, 18>.
5.Декартовым произведением множествA и B называется такое результирующее множество пар вида (x,y), построенных таким образом, что первый элемент из множества A, а второй элемент пары — из множества B. Общепринятое обозначение:
Произведения трёх и более множеств можно построить следующим образом:
Примеры
1.Положим A=<1,2>,B=<3,4>. Тогда результат декартова произведения можно записать так: A×B=<(1,3),(1,4),(2,3),(2,4)>, а B×A=
2.Если в предыдущем примере положить B=A, очевидно, что A×B=B×A=
6. Разностью множеств A и B называется множество элементов, принадлежащих A и не принадлежащих B. Обозначают AB и читают "разность A и B".
Пример 1. Пусть A есть отрезок [1, 3], B – отрезок [2, 4]; тогда объединением 
будет отрезок [1, 4], пересечением 
– отрезок [2, 3], разностью AB– полуинтервал [1, 2), BA – полуинтервал (3, 4].
Пример 2. Пусть A есть множество прямоугольников, B – множество всех ромбов на плоскости. Тогда есть множество всех квадратов, AB – множество прямоугольников с неравными сторонами, BA – множество всех ромбов с неравными углами.
7. Пересечение множеств является бинарной операцией на произвольном булеане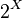 
;
§ Операция пересечения множеств коммутативна:
§ Операция пересечения множеств транзитивна:
§ Универсальное множество 
является нейтральным элементом операции пересечения множеств:
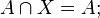
§ Таким образом булеан вместе с операцией пересечения множеств является абелевой группой;
§ Операция пересечения множеств идемпотентна:
§ Если 
— пустое множество, то 
8.Объединение множеств является бинарной операцией на произвольном булеане 
§ Операция объединения множеств коммутативна:
§ Операция объединения множеств транзитивна:
§ Пустое множество является нейтральным элементом операции объединения множеств:
§ Таким образом булеан вместе с операцией объединения множеств является моноидом;
§ Операция пересечения множеств идемпотентна:
Виды отношений
1.Бинарное отношение (двучленное отношение). Бина́рное отноше́ние в математике — двухместное отношение между любыми двумя множествами 
и 
, то есть всякое подмножество декартова произведения этих множеств: 
[1] . Бинарное отношение на множестве — любое подмножество 
, такие бинарные отношения наиболее часто используются в математике, в частности, таковы равенство, неравенство, эквивалентность, отношение порядка.
2. Тернарное отношение — то же, что трёхместное отношение (трёхчленное отношение).
3.Кватернарное отношение — то же, что четырёхместное отношение (четырёхчленное отношение)
10. Рефлексивное отношение в математике — бинарное отношение 
на множестве 
, при котором всякий элемент этого множества находится в отношении с самим собой.
Формально, отношение рефлексивно, если 
.
Свойство рефлексивности при заданных отношениях матрицей характеризуется тем, что все диагональные элементы матрицы равняются 1; при заданных отношениях графом каждый элемент х имеет петлю — дугу (х, х).
Бинарное отношение на множестве является рефлексивным тогда и только тогда, когда его подмножеством является тождественное отношение 
на множестве ( 
), то есть 
.
Если это условие не выполнено ни для какого элемента множества , то отношение называется антирефлексивным (или иррефлексивным).
Если антирефлексивное отношение задано матрицей, то все диагональные элементы являются нулевыми. При задании такого отношения графом каждая вершина не имеет петли — нет дуг вида (х, х).
Формально антирефлексивность отношения определяется как: 
.
Если условие рефлексивности выполнено не для всех элементов множества , говорят, что отношение нерефлексивно.
Примеры рефлексивных отношений
· отношение равенства 
· отношение сравнимости по модулю
· отношение параллельности прямых и плоскостей
· отношение подобия геометрических фигур;
· отношения нестрогого порядка:
· отношение нестрогого неравенства 
· отношение нестрогого подмножества 
· отношение делимости 
В математике бинарное отношение на множестве называется рефлексивным, если всякий элемент этого множества находится в отношении с самим собой.
Свойство рефлексивности при заданных отношениях матрицей характеризуется тем, что все диагональные элементы матрицы равняются 1; при заданных отношениях графом каждый элемент имеет петлю — дугу (х, х).
Если это условие не выполнено ни для какого элемента множества , то отношение называется антирефлексивным.
Если антирефлексивное отношение задано матрицей, то все диагональные элементы являются нулевыми. При задании такого отношения графом каждая вершина не имеет петли — нет дуг вида (х, х).
Формально антирефлексивность отношения определяется как: .
Если условие рефлексивности выполнено не для всех элементов множества , говорят, что отношение нерефлексивно.
Примеры рефлексивных отношений
отношение сравнимости по модулю
отношение параллельности прямых и плоскостей [ источник не указан 191 день ]
отношение подобия геометрических фигур;
отношения нестрогого порядка:
отношение нестрогого неравенства
отношение нестрогого подмножества
Примеры антирефлексивных отношений
отношения строгого порядка:
отношение строгого неравенства
отношение строгого подмножества
отношение перпендикулярности прямых (или ортогональности ненулевых векторов) в геометрии.
20. Симметричность бинарного отношения. Пример
Симметричность: для любых двух элементов а, b є М : аRb и bRа (т.е. R = R -1 ). Симметрична параллельность прямых, так как если a II b, то
b II a («быть равным»; «быть взаимнопростым»).
21. Антисимметричные бинарные отношения. Пример
Aнтисимметричность: если для а ≠ b верно отношение аRb, то ложно bRа («быть больше», «не меньше», «быть делителем»).
R = <(x,y) : x є R, у є R, х-у ≥ 1>обладает свойствами антисимметрич-ности
22. Транзитивные бинарные отношения. Пример
Транзитивность: если аRb и bRс, то аRс для любых а, b, с є М («быть больше», «быть параллельным», «быть равным»).
23. Отношение эквивалентности. Пример
Бинарное отношение a на множестве X называется отношением эквивалентности на X, если a рефлексивно, симметрично и транзитивно.
Отношение эквивалентности часто обозначают символами
,
.
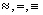Примерами отношения эквивалентности служат:
отношение тождества IX = <(a, a)|a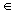
X> на непустом множестве X;
отношение параллельности на множестве прямых плоскости;
отношение подобия на множестве фигур плоскости;
отношение равносильности на множестве уравнений;
отношение "иметь одинаковые остатки при делении на фиксированное натуральное число m" на множестве целых чисел. Это отношение в математике называют отношением сравнимости по модулю m и обозначают a
b (mod m);
отношение "принадлежать одному виду" на множестве животных;
отношение "быть родственниками" на множестве людей;
отношение "быть одного роста" на множестве людей;
отношение "жить в одном доме" на множестве людей.
Отношения "жить на одной улице", "быть похожими" на множестве людей отношениями эквивалентности не являются, так как не обладают свойством транзитивности.
Из перечисленных выше свойств бинарных отношений следует, что пересечение отношений эквивалентности является отношением эквивалентности.
При помощи отношений в математике отображают некоторые связи между элементами множеств. Простейшими примерами отношений, уже рассмотренных раньше, являются отношения принадлежности х е X элемента х множеству X и отношения включения А с В, А с В подмножества А в подмножество В.
По количеству элементов, между которыми определены связи, отношения делятся на унарные (одноместные), бинарные (двухместные), тернарные (трехместные) и /7-арные (/7-местные). В унарном отношении участвует один элемент. Эти отношения называются свойствами и отождествляются с подмножеством элементов, которые этим свойством обладают. Так, например, в множестве всех положительных чисел отношение или свойство «быть четным» отождествляется с подмножеством чисел 2, 4, 6, .
В бинарных отношениях участвуют пары элементов множеств, так называемые упорядоченные пары , > х,, х2. е X, у,, у2. е ?. Упорядоченность понимается как то, что в записи на первом месте всегда стоит х е X, а на втором у е ?. Иными словами, х предшествует у.
Определение 15.1. Прямым (декартовым) произведением множеств А и В, обозначаемым Ах В, называется множество упорядоченных пар, такое, что первая координата каждой пары — элемент А, а вторая координата — элемент В, т.е. Ах В = – < аеАиЬе В>. Например, А – <1, 2>, В = <а, Ь, с).
Тогда А х В – < , , , , , >. Декартово произведение В х А – < , , , , , >. Декартово произведение А х А – < , , , >называется декартовым квадратом множества А.
Если множество А включает т различных элементов, а множество В — п элементов, то произведения множеств Ах В и В х А имеет тхп элементов. Пусть А- <1>, а В = <1,2,3>. Тогда Ах В -< , , >. Если А -0, а В – <1,2,3>. Тогда Ах В = В х А = 0.
В целях наглядного представления декартовых произведений удобно использовать язык геометрии. Для этого множества X, ? представляются осями координат. Элементы х е X, у е ? — соответственно абсциссами и ординатами. Само произведение X х ? — точками плоскости Х0?. В качестве примера на рис. 1.4 показано декартово произведение множеств X = <1, 2, 3>, ? = <1, 2>.
Рис. 1.4. Декартово произве дение множеств X, У
По аналогии с декартовым произведением двух множеств X, ? можно построить декартово произведение X х ? х Z трех множеств X, ?, Zи вообще декартово произведение X, хХ2 х . хХп п множеств X!, Х2, Xп.
Определение 16.1. Декартовым произведением 1х>"х2 трех множеств X,
?, Z называется множество всех упорядоченных троек > , составленных из элементов этих множеств так, что X х? х! = < , х е X, у е ?, г е Z>. Декартовым произведением Х хХ2 х, . хХп п множеств Хх, Х2,
Определение 17.1. Любое непустое подмножество R декартова произведения X х У множеств X, Yназывается бинарным отношением между X и У.
Записывается это так: R с X хУ, или так: xRy, или так: ? R. Слово «бинарный» происходит от английского binary, что в переводе означает «двойной».
Любое непустое подмножество X х X является бинарным отношением на X. В частности, множество X х X называется универсальным отношением на X.
Определение 18.1. Любое непустое подмножество Г декартова произведения X хУ х Z множеств X, У, Z называется тернарным отношением между X, У и Z и записывается так: Т с X хУ х Z.
Определение 19.1. Любое непустое подмножество Nдекартова произведения Хх х Х2 х, . хХп множеств Хх, X2, . Xп называется /z-арным отношением между Хх, Х2, . Х3 и записывается
Бинарное отношение R с X хУ может отражать разный смысл. Например, значениями множества X можно закодировать названия книжных издательств, а элементами множества У — всех фирм некоторого региона, которые занимаются продажей этих книг. Тогда отношению R с X хУ можно придать смысл множества заключенных договоров между издательствами и торгующими фирмами. Пусть ЛГ = <1,2, 3>, У – <1, 2>рассматриваются как три издательства и два магазина, продающие книги. Тогда отношение R – < , , >означает, что издательство 1 заключило договор с магазином 1, издательство 2 — с магазином 2, издательство 3 — с этим же магазином 2.
Примерами трехместных отношений Т с X хУ х Z могут быть такие: 1) из х видов сырья у предприятий выпускают z видов продукции; 2) х покупателей покупают у товаров по г ценам; 3) по х бомбардировщикам у ракетно-зенитных комплексов дали залп z ракетами. Аналогичным образом может придаваться смысл и /7-местным отношениям А с А, хХ2 х . х Xп.
Рассмотрим свойства бинарных отношений.
Определение 20.1. Отношение Я на множестве Сможет быть:
- 1) рефлексивным;
- 2) антирефлексивным;
- 3) симметричным;
- 4) асимметричным;
- 5) антисимметричным;
- 6) транзитивным.
Определение 21.1. Отношение Я на множестве X является рефлексивным, если оно выполняется между самим элементом, т.е. хЯх. Например, в отношениях «х имеет общий признак с у», «х похож на у» имеет место хЯх, так как элемент х похож на самого себя.
Определение 22.1. Отношение Я на множестве X является антирефлексивным, если хЯх не выполняется ни для одного х е X. Например, в отношениях «брат х старше брата у», «операция х выполняется раньше операции у», хЯх не выполняется, так как брат х не может быть старше себя, а операция х начаться раньше самой себя.
Определение 23.1. Отношение Я на множестве ^является симметричным, если для всех х, у е X из хЯу следует уЯх. Например,
в отношениях «х похож на у», «операция х несовместима с операцией у» имеет место как хЯу, так и уЯх. Действительно, если х похож на у, то у похож на х, если операция х несовместима с у, то операция у несовместима с х.
Определение 24.1. Отношение Я на множестве X является асимметричным, если из двух соотношений хЯу, уЯх одно не выполнено для всех х, у е X. Например, в отношениях «х подчиняется у», «операция х выполнена раньше операции у» имеет место хЯу, но не выполняется уЯх.
Определение 25.1. Отношение Я на множестве ^является ан-тисиммитричным, если соотношения хЯу и уЯх выполняются тогда и только тогда, когда х – у для всех х, у е X. Например, в отношении «операция х является частью операции у» имеет место хЯу и уЯх только тогда, когда х – у.
Определение 26.1. Отношение Я на множестве X является транзитивным, если для всех х, у, г. е X из соотношений хЯу, уЯ1
следует хЯг. Например, в отношении «операция х предшествует операции у, а операция у предшествует операции г» из хЯу и уЯ1 следует хЯ1.
На практике весьма часто приходится иметь дело с отношением эквивалентности, близким ему отношением толерантности и различными отношениями порядка.
По смыслу отношение эквивалентности определяется как «элементы х и у одинаковы», «элементы х и у взаимозаменяемы».
Определение 27.1. Отношение Я на множестве X называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.
Действительно, в этом отношении каждый элемент эквивалентен самому себе (рефлексивность). Если элемент х эквивалентен элементу у, то и элемент у эквивалентен элементу х (симметричность). Если элемент х эквивалентен элементу у, а элемент у эквивалентен элементу г, то элемент х эквивалентен элементу г. (транзитивность).
Типичным примером отношения эквивалентности является отношение равенства (=) на множестве чисел. Очевидно, что любое число а из множества действительных чисел равно самому себе. Если а – Ь, то Ь = а. Если а = Ь, а Ь = с, то а = с.
Другими примерами отношения эквивалентности могут быть отношения параллельности прямых в эвклидовой плоскости, отношения проживания в одном доме жителей города. Последний из приведенных примеров наглядно иллюстрирует основное свойство отношения эквивалентности.
Это отношение разбивает любое множество на непересекаю-щиеся подмножества (классы эквивалентности). В данном случае все жители города разбиваются на жителей, живущих в одних и тех же домах. В результате получим столько классов эквивалентности, сколько домов, в которых проживают люди. Таким образом, если — /’-й класс / е /, а М — множество жителей, то и/е/ М-, = М, М, П М> =0 для всех /, у е /, где / — множество классов.
Определение 28.1. Отношение Я на множестве ^называется отношением толерантности, если оно рефлексивно и симметрично.
Например, отношение «игрок х играет сам с собой в шахматы и с другом у» есть отношение толерантности, так как хЯх, а хЯу влечет уЯх.
Определение 29.1. Отношение Я на множестве X называется отношением нестрого порядка, если оно рефлексивно, антисимметрично и транзитивно.
Отношения на множестве чисел ^являются отношениями нестрогого порядка, так как любое число х е X равно самому себе (рефлексивность).
Для любой пары чисел х, у е X при а Ь не выполняется Ь> а (антисимметричность). Для любой тройки чисел х, у, I е X, если а Ь, Ь > с, то а > с (транзитивность).
Определение 30.1. Отношение Я на множестве X называется отношением строго порядка, если оно антирефлексивно, антисимметрично и транзитивно.
Отношения на множестве чисел ^являются отношениями строгого порядка, так как любое число х е X не может быть меньше или больше самого себя (антирефлексивность). Для любой пары чисел х, у е X при х у не выполняется у > х (антисимметричность). Для любой тройки чисел х, у, 1 е X, если х у, а у > г, то х > 1 (транзитивность).
Определение 31.1. Множество X с заданным на нем отношением нестрогого или строгого порядка Я называется упорядоченным и обозначается парой .
Определение 32.1. Если для каждой пары х, у е X справедливо
отношение строгого или нестрогого порядка, то множество называется полностью упорядоченным. В противном случае множество называется частично упорядоченным.
Определение 33.1. Строгий или нестрогий порядок, заданный на полностью упорядоченном множестве , называется линейным порядком.
Все множества чисел линейно упорядочены, так как для любых чисел из этих множеств одно меньше другого или они равны.
Множество букв русского или латинского алфавита линейно упорядочено отношением предшествования, или, что то же, отношением следования.
Отношение подчиненности на некотором предприятии определяет строгий частичный порядок, так как в нем несравнимы сотрудники разных отделов.