Рассмотрим цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки индуктивности.
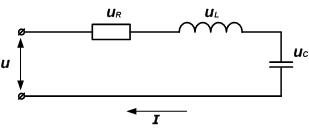
Напряжение на зажимах цепи
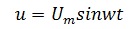
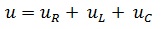
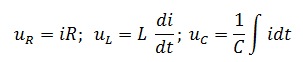
Выполнив подстановку, получим
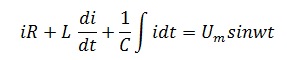
Подставим в последнее выражение ток в цепи, зная, что он равен
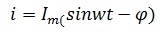
В итоге получим выражение
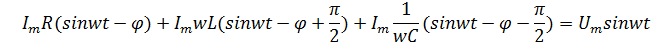
Из этого выражения можно увидеть сдвиг фаз каждого элемента. У резистора он отсутствует, то есть напряжение и ток совпадают по фазе, у катушки индуктивности напряжение опережает ток на угол π/2, а у конденсатора, напротив, отстает.
Сдвиг фаз RLС-цепи можно определить по формуле
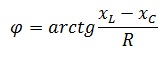
Полное сопротивление RLС-цепи
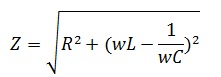
Амплитудное значение тока
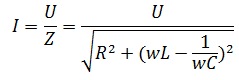
При построении векторной диаграммы RLC-цепи возможны три случая:
1 – Цепь носит активный характер, сдвиг фаз равен нулю, индуктивное и емкостное сопротивления равны. При этом в такой цепи наблюдается резонанс напряжений.
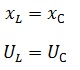
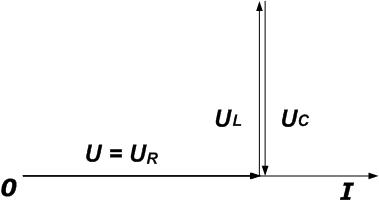
2 – Цепь носит индуктивный характер, в этом случае индуктивное сопротивление больше чем емкостное.
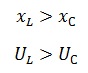
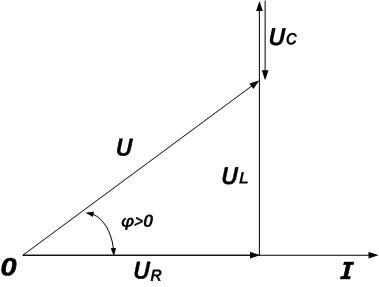
На векторной диаграмме, как правило, сначала откладывают вектор напряжения на катушке индуктивности, а затем из него вычетают напряжение на конденсаторе. После этого проводят вектор общего напряжения и определяют сдвиг фаз φ.
3 – Цепи носит емкостной характер, при этом емкостное сопротивление больше чем индуктивное.
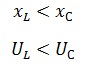
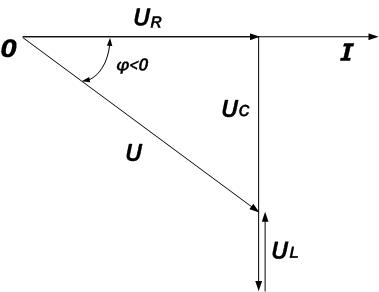
Построение векторной диаграммы выполняется аналогично цепи индуктивного характера, за тем исключением, что здесь сдвиг фаз отрицателен и вычитается индуктивное напряжение из напряжения на емкости.
Цепь состоит из последовательно включенных резистора сопротивлением 25 Ом, конденсатора емкостью 200 мкФ и катушки индуктивности 30 мГн. Ток, протекающий в цепи, равен 0,75 А. Определите U,UR,UL,UC,φ. Постройте векторную диаграмму и определите характер цепи.
Найдем напряжение на каждом из элементов
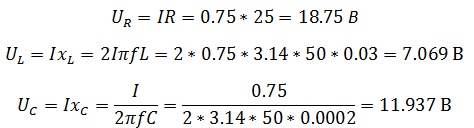
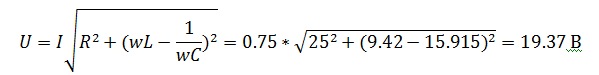
Сдвиг фаз равен
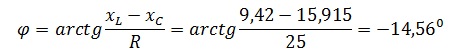
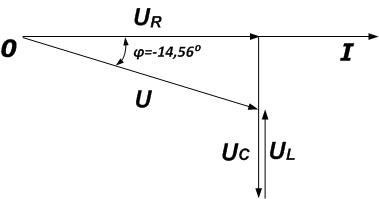
Из векторной диаграммы можно сделать вывод, что цепь носит емкостной характер.
Рассмотрим цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки индуктивности.

Напряжение на зажимах цепи
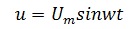
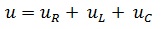
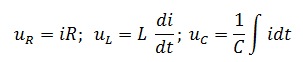
Выполнив подстановку, получим
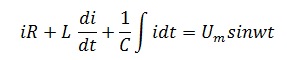
Подставим в последнее выражение ток в цепи, зная, что он равен
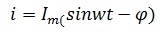
В итоге получим выражение
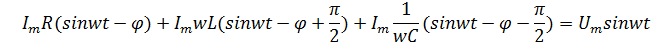
Из этого выражения можно увидеть сдвиг фаз каждого элемента. У резистора он отсутствует, то есть напряжение и ток совпадают по фазе, у катушки индуктивности напряжение опережает ток на угол π/2, а у конденсатора, напротив, отстает.
Сдвиг фаз RLС-цепи можно определить по формуле
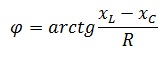
Полное сопротивление RLС-цепи
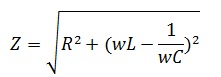
Амплитудное значение тока
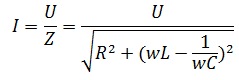
При построении векторной диаграммы RLC-цепи возможны три случая:
1 – Цепь носит активный характер, сдвиг фаз равен нулю, индуктивное и емкостное сопротивления равны. При этом в такой цепи наблюдается резонанс напряжений.
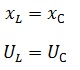

2 – Цепь носит индуктивный характер, в этом случае индуктивное сопротивление больше чем емкостное.
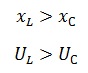

На векторной диаграмме, как правило, сначала откладывают вектор напряжения на катушке индуктивности, а затем из него вычетают напряжение на конденсаторе. После этого проводят вектор общего напряжения и определяют сдвиг фаз φ.
3 – Цепи носит емкостной характер, при этом емкостное сопротивление больше чем индуктивное.
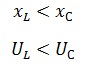

Построение векторной диаграммы выполняется аналогично цепи индуктивного характера, за тем исключением, что здесь сдвиг фаз отрицателен и вычитается индуктивное напряжение из напряжения на емкости.
Цепь состоит из последовательно включенных резистора сопротивлением 25 Ом, конденсатора емкостью 200 мкФ и катушки индуктивности 30 мГн. Ток, протекающий в цепи, равен 0,75 А. Определите U,UR,UL,UC,φ. Постройте векторную диаграмму и определите характер цепи.
Найдем напряжение на каждом из элементов
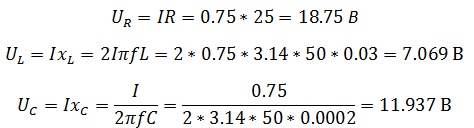
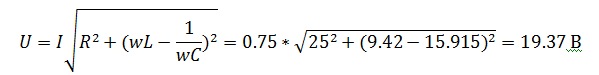
Сдвиг фаз равен
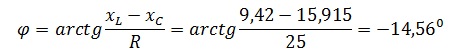

Из векторной диаграммы можно сделать вывод, что цепь носит емкостной характер.
 |
|
 |
Начнем нашу лекцию с рассмотрения цепи переменного тока, состоящей из последовательно соединенного резистора R и катушки индуктивности L.
При этом напряжение приложенное к схеме определяется по следующей формуле: В соответствии со вторым законом Кирхгофа можно записать: Тогда напряжение на сопротивлении и катушке индуктивности равно:
Отсюда напряжение, приложенное к последовательной цепи LR определяется по следующей формуле:
Поэтому ток протекающий в такой цепи равен: Подставив ток в формулу для напряжения, в результате получим:
Из выражений выше, хорошо видно, что первое слагаемое это напряжение на сопротивлении, то есть: Из этого выражения можно легко сделать вывод о том, что напряжение и ток в резисторе совпадают по фазе. Посмотрим, что происходит с напряжением на индуктивности:
Таким образом напряжение на катушке опережает ток на угол: Как мы уже знаем, реактивное сопротивление катушки индуктивности равно: Индуктивное сопротивление катушки зависит от частоты. При постоянном токе, она равна нулю, а поэтому и сопротивление тоже. Сдвиг фаз в последовательной RL-цепи можно вычислить по формуле:
Отсюда, формула полного сопротивления RL-цепи, выглядит так:
Тогда амплитудное значение тока определим так:
|
Рассмотрим последовательную RC-цепь, состоящую из двух компонентов, а именно – последовательно соединенных резистора и конденсатора.

Напряжение приложенное к схеме в этом случае определяется по формуле:
Из второго закона Кирхгофа можно записать это же напряжение как сумму падений напряжений на резисторе и емкости.

Тогда протекающий ток в схеме равен
Подставив этот промежуточный результат в выражение выше, и осуществив интегрирование, получим:

При этом напряжение на резисторе и конденсаторе будет равно:

Как видно из последней формулы напряжение на емкости отстает от тока на угол:
Реактивное емкостное сопротивление конденсатора находим по формуле:

Как видим с снижением частоты емкостное сопротивление возрастает. При постоянном токе оно будет стремиться к бесконечности, так как частота тока будет равна нулю.
Сдвиг фаз, полное сопротивление, амплитудное значение тока в последовательной RC – цепи переменного тока можно вычислить по формулам ниже:

 |
Рассмотрим более сложный случай, состоящий из последовательно соединенных резистора, катушки индуктивности и конденсатора.

Напряжение на зажимах схемы будет:

Выполнив подстановку, можно записать так:

Подставим в эту формулу ток протекающий в цепи, получим
В финале увидим такую длинную формулу:

Отсюда легко можно увидеть сдвиг фаз каждого компонента. У сопротивления он отсутствует, то есть ток и напряжение полностью совпадают по фазе, у индуктивности напряжение опережает ток на угол 3,14/2, а у конденсатора, наоборот, отстает на этот угол.
Сдвиг фаз, полное сопротивление и амплитудное значение тока RLС-цепи можно вычислить по формулам ниже:

При построении ВД RLC-цепи возможны три варианта:
 |








