 При повторении импульсных вторичных источников питания и стабилизаторов напряжения или самостоятельной их разработке радиолюбители испытывают трудности при подборе магнито-проводов и расчете индуктивных элементов устройств. Публикуемая статья может помочь в решении таких задач.
При повторении импульсных вторичных источников питания и стабилизаторов напряжения или самостоятельной их разработке радиолюбители испытывают трудности при подборе магнито-проводов и расчете индуктивных элементов устройств. Публикуемая статья может помочь в решении таких задач.
В однотактных импульсных источниках питания и стабилизаторах напряжения важнейшим элементом является дроссель или импульсный трансформатор, в котором происходит накопление энергии. Обычно их наматывают на броневых или Ш-образных феррито-вых магнитопроводах с зазором или кольцах из Мо-пермаллоя МП140 или МП160 [1 — 4]. Магнитопрово-ды из прессованного пермаллоя (Mo-пермаллоя) достаточно дороги и дефицитны. В то же время в большинстве случаев индуктивные элементы таких устройств можно выполнить на широко распространенных кольцах из феррита с проницаемостью 600. . .6000. если в них ввести зазор.
Индуктивность L катушки, намотанной на кольцевом магнитопроводе, как известно, можно найти по формуле [1]
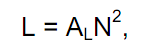
где AL — так называемый коэффициент индуктивности, N — число витков катушки. Коэффициент AL соответствует индуктивности катушки в один виток и обычно приводится в справочных данных конкретных магнитопроводов [1 — 4], а для кольцевых магнитопроводов может быть легко рассчитан;
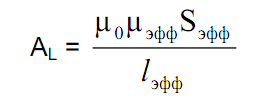
где μo = 1,257-10 -3 мкГн/мм — абсолютная магнитная проницаемость вакуума, μэфф — эффективная начальная магнитная проницаемость материала магнитопровода. Sэфф — эффективная площадь сечения магнитопровода в мм 2 , l эфф — эффективная длина магнито-провода в мм.
Зная величину AL, нетрудно определить число витков катушки для получения необходимой индуктивности:
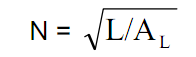
Эффективное сечение и длина магнитопровода несколько меньше определяемых по его геометрическим параметрам и обычно приводятся в справочной литературе. В табл. 1 в первых пяти столбцах приведены геометрические размеры, эффективные сечение и длина l эфф Для ферритовых колец стандартного ряда с внешним диаметром D от 6 до 50 мм, внутренним d и высотой h [1].
В этой же таблице приведены расчетные значения площади окна магнитопроводов SОKH, периметра сечения р и коэффициента индуктивности AL для μэфф = 50. Данные позволяют рассчитать индуктивность любой катушки, намотанной на кольцевом магнитопроводе с табличными геометрическими размерами. Если μэфф используемого кольца отличается от 50, значение AL необходимо пропорционально изменить, например, для μэфф = 2000 коэффициент AL следует увеличить в 40 раз. Следует иметь ввиду, что значения μэфф , Sэфф и l эфф определяются с большой погрешностью, и в справочниках для кольцевых магнитопроводов указан обычно двукратный разброс значений АL[1]. Поэтому величины AL, взятые из Таблицы 1, следует принимать как ориентировочные и уточнять их при необходимости более точного расчета по результатам эксперимента.
Для этого следует намотать на магнитопроводе пробную катушку, например, из десяти витков и измерить ее индуктивность LПР. Здесь себя хорошо зарекомендовал прибор, описанный в [5]. Разделив LПР на 100 = 10 2 , определим значение AL. Расчетное значение N следует увеличить на несколько витков (до N1), по результату измерения L1 уточнить необходимое число витков 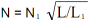 , и отмотать лишние витки.
, и отмотать лишние витки.
Описанным выше образом можно рассчитать индуктивность катушки или необходимое число витков. Однако, как только речь заходит о дросселях для импульсных источников питания, сразу возникает вопрос, какой ток может выдержать дроссель без насыщения магнитопровода?
Магнитная индукция В в магнитопроводе при токе I может быть рассчитана по формуле
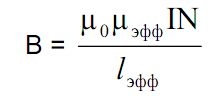
Максимально допустимая индукция Втах для материалов магнитопроводов приводится в справочных данных и лежит в пределах 0, 25. ..0,5 Тл. Из этой формулы несложно получить выражение для максимального тока дросселя:
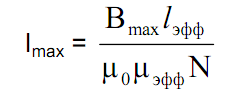
Если в нее подставить формулу для определения числа витков по заданной индуктивности, получим
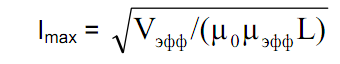
где /эфф = Sэфф lэфф— эффективный объем магнитопровода. Нетрудно видеть, что чем выше μэфф, тем меньший ток может пропустить дроссель при тех же геометрических размерах магнитопровода и заданной индуктивности. Более или менее приемлемые результаты при изготовлении дросселей для ИВЭП получаются при μэфф = 30. 50. Именно поэтому в Таблице 1 значение коэффициента AL приведено для μэфф = 50. В той же таблице приведено максимальное значение тока lmax через дроссель с одним витком при Вmax = 0,3 Тл. Для определения допустимого тока реального дросселя достаточно табличное значение lmax разделить на число витков N.
Однако в радиолюбительской практике более доступны кольцевые магнитопроводы с большими значениями эффективной магнитной проницаемости μэфф = 600. 6000. Понизить эффективную магнитную проницаемость таких магнитопроводов можно введением зазора, при этом
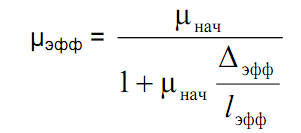
где μнач — начальная магнитная проницаемость материала магнитопровода, Δэфф — эффективная ширина зазора. При реальной ширине зазора μэфф = lэфф/Δэфф. Для того, чтобы снизить μэфф примерно до 50. . . 100 (это значение исходя из опыта расчета и изготовления дросселей близко к оптимальному), эффективная ширина зазора должна составлять Δэфф = lэфф/(50. 100) независимо от начальной магнитной проницаемости магнитопровода.
Если в вышеприведенную формулу для расчета AL подставить значение μэфф для магнитопровода с зазором,получим
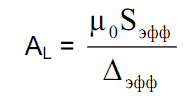
Еще более простой получается формула для максимального тока через дроссель
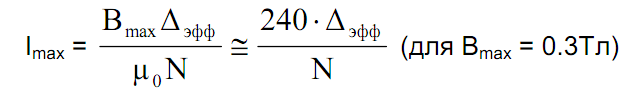
т. е. допустимый ток определяется только эффективным зазором и числом витков.
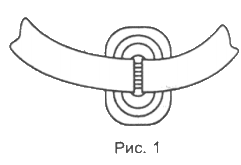 Почти все приведенные выше формулы уже были опубликованы в журнале «Схемотехника» [4], однако ни в одной из известных автору статьи публикаций не отмечено, что эффективная ширина зазора, которую надо применять в расчетах, меньше геометрической. Это различие возникает из-за того, что магнитное поле, существующее рядом с зазором (Рис. 1), шунтирует зазор и уменьшает его эффективную ширину. Для того, чтобы рассчитать влияние этого поля, можно обратиться к аналогии между магнитным и электрическим полями. Воспользуемся формулой для емкости конденсатора из двух цилиндров с близко расположенными торцами [6]:
Почти все приведенные выше формулы уже были опубликованы в журнале «Схемотехника» [4], однако ни в одной из известных автору статьи публикаций не отмечено, что эффективная ширина зазора, которую надо применять в расчетах, меньше геометрической. Это различие возникает из-за того, что магнитное поле, существующее рядом с зазором (Рис. 1), шунтирует зазор и уменьшает его эффективную ширину. Для того, чтобы рассчитать влияние этого поля, можно обратиться к аналогии между магнитным и электрическим полями. Воспользуемся формулой для емкости конденсатора из двух цилиндров с близко расположенными торцами [6]:
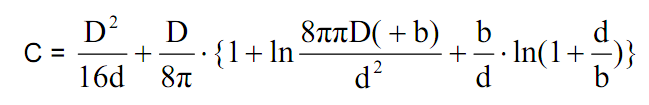
где С — емкость конденсатора в сантиметрах, D— диаметр цилиндров, b — их высота, d — зазор между их торцами.
Нетрудно заметить, что первое слагаемое соответствует емкости зазора между цилиндрами, а второе— емкости, вносимой боковыми поверхностями цилиндров. Будем считать, что высота цилиндров равна их удвоенному диаметру b = 2D. Это означает, что мы учтем только емкость ближайшей к зазору части боковой поверхности цилиндров, пренебрегая дальней. Расчеты при длине цилиндров в 3 или 4 диаметра дают практически тот же результат.
Для того, чтобы в дальнейшем перейти от емкости между цилиндрами к емкости между прямоугольными брусками (а это по форме ближе к сечению ферритового кольца), будем считать, что емкость, вносимая боковыми поверхностями, пропорциональна периметру зазора, и выразим в этой формуле диаметр цилиндров через периметр р их кругового сечения:
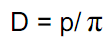
высота цилиндров b = 2D = 2р/тг.
Если в формулу для емкости подставить эти выражения, можно определить из нее отношение полной емкости к емкости между торцами в функции от отношения зазора к периметру цилиндров β = d/b. Формула эта, однако, получается довольно громоздкой и неудобной для применения.
Обозначим буквой а отношение эффективного зазора, обеспечивающего без емкости боковых поверхностей ту же емкость, что и емкость между торцами с учетом емкости боковых поверхностей, к геометрическому. На Рис. 2 приведена расчетная зависимость а от β. Из подобия уравнений, описывающих электрическое и магнитное поле, следует, что аналогично выглядит и зависимость отношения эффективного магнитного зазора к геометрическому от отношения геометрического магнитного зазора к периметру.
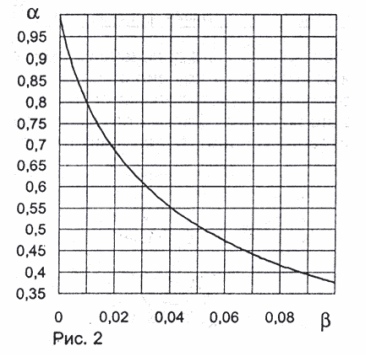
Из графика на Рис. 2 следует, что эффективная ширина зазора может существенно отличаться от геометрической. В реальном диапазоне β составляет от 0,01 до 0,1 эффективная ширина зазора меньше геометрической в 1,26. 2,66 раза.
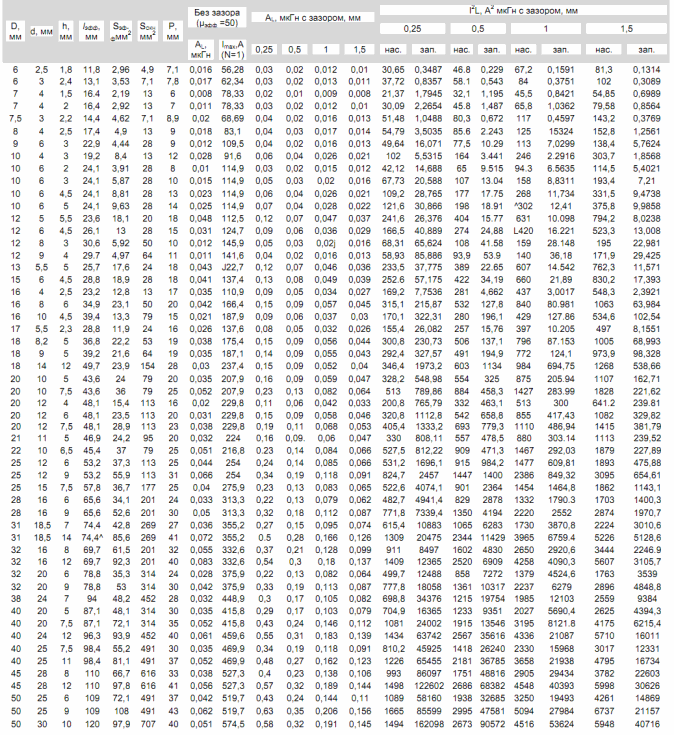
В Таблице 1 приведены значения AL для кольцевых магнитопроводов с четырьмя различными зазорами, рассчитанные с учетом отличия эффективного зазора от геометрического.
Вышесказанное позволяет сделать вывод, что необходимые число витков и зазор практически не зависят от начальной магнитной проницаемости материала магнитопровода, и поэтому можно применить ферриты с любой проницаемостью, большей 600. Для любого имеющегося кольца с табличным зазором по значению AL нетрудно вычислить индуктивность или необходимое число витков и рассчитав β = Δ/р, по графику (рис. 2) определить значение а = Δэфф /р и Δэфф = ap. По найденному значению Δэфф и приведенной ранее формуле можно найти максимальный ток, не вызывающий насыщения сердечника.
Однако существует еще одно обстоятельство, влияющее на выбор магнитопровода — возможность намотки на него требуемого числа витков проводом соответствующего сечения. Необходимая площадь окна кольца составляет
Sокн = NSпров/Кзап
где Sпров — сечение провода, а kзап — коэффициент заполнения окна. Расчет Sпров производят по формуле Sпров = l/j . где j — допустимая плотность тока. Типовое значение kзап по меди составляет 0,3, а для j при начальном расчете принимают значение 2,5 А/мм2.
Подставив в формулу для расчета площади окна выражения для N и АL, получим следующую формулу:
I 2 L = (Sокнjkзап) 2 μSэфф/Δэфф
Подобное выражение можно получить и из формулы для максимального тока, который можно пропустить через дроссель без насыщения сердечника:
I 2 L = Bmax 2 Sэфф lэфф ( μ μэфф )
Однозначного расчета конструктивных параметров дросселя по заданной индуктивности и току не существует. Однако при подборе кольца и определении данных обмотки могут помочь последние восемь колонок табл. 1 . В них приведены максимальные значения произведения l 2 L по насыщению и по заполнению, рассчитанные по приведенным выше формулам для Вmах = 0,3 Тл, kзan = 0,3, j = 2,5 А/мм 2 и четырех значений зазора.
Подбор колец и расчет конструктивных параметров дросселей продемонстрируем на двух примерах.
Пусть необходим дроссель индуктивностью 22 мкГн на рабочий ток 1,2 А. Для него значение l 2 L = 1,22х22 = 31,68. Среди колец минимального диаметра первым почти подходит кольцо К10x6x4,5. При введении в него зазора 0,25 мм имеем возможность намотать дроссель с большим запасом по току (Таблица 1, колонка «нас»), но с некоторым превышением плотности тока относительно 2,5 А/мм 2 (колонка «зап.»).
Определим параметры дросселя при зазоре 0,25 мм. Для него коэффициент индуктивности по Таблице 1 составит AL = 0,064, необходимое число витков
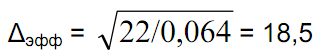
(округляем до 19), допустимый ток Для I = 1,2 А при j = 2,5 А/мм2 необходим провод сечением
Sпров = I/j = 1,2/2,5 = 0,48mm 2
При коэффициенте заполнения kзап = 0,3 необходимая площадь окна составит
Площадь окна по Таблице 1 составляет 28,3 мм 2 , что несколько меньше. Необходимо за счет увеличения плотности тока уменьшить сечение провода до
Sпров = Sокн kзап/N = 28,3×0,3/19 = 0,446 мм 2
Плотность тока составит j = I/Sпров = 1,2/0,446 = =2,68 А/мм 2 , что вполне допустимо. Диаметр провода указанного сечения (по меди) можно рассчитать по формуле:
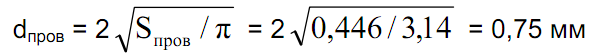
Пусть необходим дроссель 88 мкГн на ток 1,25 А. Для него l 2 L = 137,5. Дроссель можно намотать на кольце К12x6x4,5 с тем же зазором, при этом насыщения магнитопровода происходить не будет, но плотность тока существенно превысит норму. Поэтому необходимо перейти к кольцу большего размера. В распоряжении автора были кольца К12x8x3 из феррита М4000НМ. На одном кольце невозможно намотать необходимый дроссель, ни по насыщению сердечника, ни по заполнению окна. Можно сложить два кольца вместе. В этом случае эффективное сечение магнитопровода увеличивается в два раза, а допустимые значения l 2 L вырастут по насыщению несколько более, а по заполнению несколько менее, чем в два раза. Поэтому необходимый дроссель при геометрическом зазоре 0,25 мм можно намотать с запасом по току насыщения и с небольшим превышением плотности тока.
Только табличными сведениями теперь не обойтись, необходим полный расчет. Для двух колец периметр сечения (при зазоре 0,25 мм):
р = D-d+4xh = 12-8+4×3 = 16 мм,
β=Δ/р = 0,25/16 = 0,0156.
По графику на Рис. 2 находим а = 0,73, откуда эффективный зазор
Δэфф = Δа = 0,25×0,73 = 0,183 мм.
Найденное значение
AL= μSэфф/Δэфф = 1,257х10 -3 х2х5,92/0,183 = 0,081
Необходимое число витков
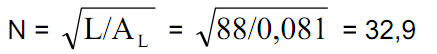
округляем в большую сторону до 33 витков. Максимальный ток через дроссель
lmax = 240 Δэфф /N = 240×0,183/33 = 1,33 А.
Максимальное сечение провода
Sпров = Sокн kзап/N = 50,3×0,3/33 = 0,457 мм 2 ,
что соответствует плотности тока 1,25/0,457 = 2,74 А/мм 2 . Сечению Sпров = 0,457 мм 2 соответствует диаметр:
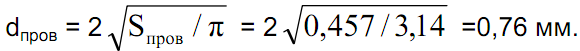
Иногда удобнее ввести два одинаковых зазора. В этом случае табличное значение AL для половинного зазора следует уменьшить в два раза, а табличное значение I 2 L для половинного зазора — удвоить.
Технология введения зазора такова. Небольшое кольцо перед намоткой разломить на две части, надпилив его надфилем, лучше алмазным. Половинки склеивают между собой эпоксидным клеем с наполнителем, в качестве которого удобно использовать тальк. При склеивании в один из зазоров или в оба на часть глубины вводят прокладку из гетинакса, текстолита или нескольких слоев бумаги. Можно считать, что толщина одного листа бумаги для ксероксов и лазерных принтеров составляет 0,1 мм. Для сохранения формы кольца в процессе полимеризации клея оно должно лежать на обрезке органического стекла, от которого затем легко отделяется при изгибе этого обрезка. Перед намоткой острые грани колец следует тщательно скруглить небольшим наждачным камнем.
У большого кольца зазор можно также выполнить ножовкой с алмазным полотном, однако его ширина при этом однозначно определяется толщиной полотна. В такой зазор для сохранения прочности кольца следует вклеить прокладку из жесткого диэлектрика.
Для экспериментальной проверки тока насыщения дросселей автором была изготовлена приставка к осциллографу, схема которой приведена на Рис. 3. Устройство представляет собой упрощенный вариант обратноходового преобразователя.
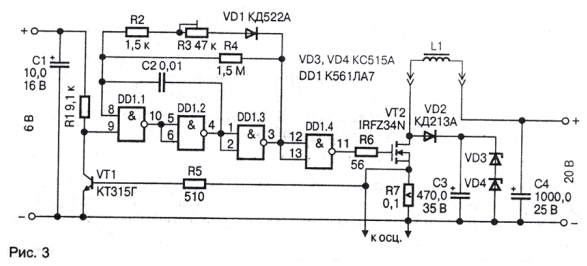
На микросхеме DD1 собран генератор импульсов положительной полярности длительностью, регулируемой в пределах 10. 300 мкс с периодом повторения около 10 мс. Импульсы с его выхода поданы на затвор мощного, но низковольтного и относительно недорогого полевого транзистора VT2. Транзистор открывается и через проверяемую катушку индуктивности L1 начинает течь линейно нарастающий ток. Когда импульс заканчивается, накопленная энергия передается через диод VD2 в нагрузку, которой служат стабилитроны VD3 и VD4. Напряжение с резистора R7, пропорциональное току через катушку L1, подается на осциллограф. Для синхронизации осциллографа лучше использовать сигнал с выхода DD1.4. Если ток превысит 6А, откроется транзистор VT1 и оборвет формирование импульса. Пока сердечник катушки не входит в насыщение, зависимость тока от времени, как указывалось выше, носит линейный характер. При плавном увеличении длительности импульсов и подходе максимального тока через дроссель к току насыщения на экране осциллографа хорошо видно резкое отклонение зависимости от линейной. Источник напряжением 20 В должен допускать выходной ток не менее 1 А. Для упрощения пользования приставкой можно цепь +6 В питать от цепи +20 В через микросхемный стабилизатор КР145ЕН5Б(Г), либо КР1157ЕН6 с любыми суффиксами (7806 или 78L06). Экспериментальная проверка изготовленных дросселей подтвердила точность расчета необходимого числа витков и тока насыщения порядка ±10 %, что можно считать неплохим результатом, учитывая ошибки установки ширины зазора и множество допущений при выводе формул
Литература:
1. И. Н. Сидоров, А. А. Христинин, С. В. Скорняков. Малогабаритные магнитопроводы и сердечники. Справочник.— М.: Радио и связь, 1989, с. .384,
2. А. Миронов. Магнитные материалы и магнитопроводы для импульсных источников питания.— Радио, 2000, №6, с. 53, 54.
3. Ферритовые магнитопроводы серии RM фирмы EPCOS. — Радио, 2001, №3, с. 49—51, №10, с. 48—50.
4. А. Кузнецов. Трансформаторы и дроссели для импульсных источников питания. — Схемотехника, 2000, №1, с. 30—33, №2, с. 48, 49, 2001, №1, с. 32—34.
5. С. Бирюков. Цифровой измеритель RCL. — Радио, 1996, №3, с. 38—41, №7, с. 62, 1997, №7, с. 32, 1998, №5, с. 63, 2001, №5, с. 44.
6. Г. Г. Гинкин. Справочник по радиотехнике. Изд. 4-е, переработанное. — М.: Госэнергоиздат, 1948, с. 816.
 При повторении импульсных вторичных источников питания и стабилизаторов напряжения или самостоятельной их разработке радиолюбители испытывают трудности при подборе магнито-проводов и расчете индуктивных элементов устройств. Публикуемая статья может помочь в решении таких задач.
При повторении импульсных вторичных источников питания и стабилизаторов напряжения или самостоятельной их разработке радиолюбители испытывают трудности при подборе магнито-проводов и расчете индуктивных элементов устройств. Публикуемая статья может помочь в решении таких задач.
В однотактных импульсных источниках питания и стабилизаторах напряжения важнейшим элементом является дроссель или импульсный трансформатор, в котором происходит накопление энергии. Обычно их наматывают на броневых или Ш-образных феррито-вых магнитопроводах с зазором или кольцах из Мо-пермаллоя МП140 или МП160 [1 — 4]. Магнитопрово-ды из прессованного пермаллоя (Mo-пермаллоя) достаточно дороги и дефицитны. В то же время в большинстве случаев индуктивные элементы таких устройств можно выполнить на широко распространенных кольцах из феррита с проницаемостью 600. . .6000. если в них ввести зазор.
Индуктивность L катушки, намотанной на кольцевом магнитопроводе, как известно, можно найти по формуле [1]
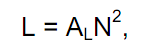
где AL — так называемый коэффициент индуктивности, N — число витков катушки. Коэффициент AL соответствует индуктивности катушки в один виток и обычно приводится в справочных данных конкретных магнитопроводов [1 — 4], а для кольцевых магнитопроводов может быть легко рассчитан;
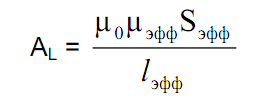
где μo = 1,257-10 -3 мкГн/мм — абсолютная магнитная проницаемость вакуума, μэфф — эффективная начальная магнитная проницаемость материала магнитопровода. Sэфф — эффективная площадь сечения магнитопровода в мм 2 , l эфф — эффективная длина магнито-провода в мм.
Зная величину AL, нетрудно определить число витков катушки для получения необходимой индуктивности:
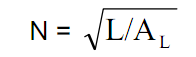
Эффективное сечение и длина магнитопровода несколько меньше определяемых по его геометрическим параметрам и обычно приводятся в справочной литературе. В табл. 1 в первых пяти столбцах приведены геометрические размеры, эффективные сечение и длина l эфф Для ферритовых колец стандартного ряда с внешним диаметром D от 6 до 50 мм, внутренним d и высотой h [1].
В этой же таблице приведены расчетные значения площади окна магнитопроводов SОKH, периметра сечения р и коэффициента индуктивности AL для μэфф = 50. Данные позволяют рассчитать индуктивность любой катушки, намотанной на кольцевом магнитопроводе с табличными геометрическими размерами. Если μэфф используемого кольца отличается от 50, значение AL необходимо пропорционально изменить, например, для μэфф = 2000 коэффициент AL следует увеличить в 40 раз. Следует иметь ввиду, что значения μэфф , Sэфф и l эфф определяются с большой погрешностью, и в справочниках для кольцевых магнитопроводов указан обычно двукратный разброс значений АL[1]. Поэтому величины AL, взятые из Таблицы 1, следует принимать как ориентировочные и уточнять их при необходимости более точного расчета по результатам эксперимента.
Для этого следует намотать на магнитопроводе пробную катушку, например, из десяти витков и измерить ее индуктивность LПР. Здесь себя хорошо зарекомендовал прибор, описанный в [5]. Разделив LПР на 100 = 10 2 , определим значение AL. Расчетное значение N следует увеличить на несколько витков (до N1), по результату измерения L1 уточнить необходимое число витков 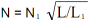 , и отмотать лишние витки.
, и отмотать лишние витки.
Описанным выше образом можно рассчитать индуктивность катушки или необходимое число витков. Однако, как только речь заходит о дросселях для импульсных источников питания, сразу возникает вопрос, какой ток может выдержать дроссель без насыщения магнитопровода?
Магнитная индукция В в магнитопроводе при токе I может быть рассчитана по формуле
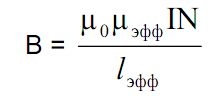
Максимально допустимая индукция Втах для материалов магнитопроводов приводится в справочных данных и лежит в пределах 0, 25. ..0,5 Тл. Из этой формулы несложно получить выражение для максимального тока дросселя:
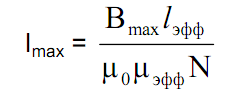
Если в нее подставить формулу для определения числа витков по заданной индуктивности, получим
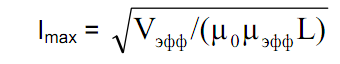
где /эфф = Sэфф lэфф— эффективный объем магнитопровода. Нетрудно видеть, что чем выше μэфф, тем меньший ток может пропустить дроссель при тех же геометрических размерах магнитопровода и заданной индуктивности. Более или менее приемлемые результаты при изготовлении дросселей для ИВЭП получаются при μэфф = 30. 50. Именно поэтому в Таблице 1 значение коэффициента AL приведено для μэфф = 50. В той же таблице приведено максимальное значение тока lmax через дроссель с одним витком при Вmax = 0,3 Тл. Для определения допустимого тока реального дросселя достаточно табличное значение lmax разделить на число витков N.
Однако в радиолюбительской практике более доступны кольцевые магнитопроводы с большими значениями эффективной магнитной проницаемости μэфф = 600. 6000. Понизить эффективную магнитную проницаемость таких магнитопроводов можно введением зазора, при этом
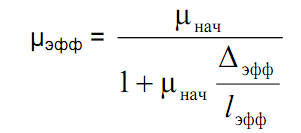
где μнач — начальная магнитная проницаемость материала магнитопровода, Δэфф — эффективная ширина зазора. При реальной ширине зазора μэфф = lэфф/Δэфф. Для того, чтобы снизить μэфф примерно до 50. . . 100 (это значение исходя из опыта расчета и изготовления дросселей близко к оптимальному), эффективная ширина зазора должна составлять Δэфф = lэфф/(50. 100) независимо от начальной магнитной проницаемости магнитопровода.
Если в вышеприведенную формулу для расчета AL подставить значение μэфф для магнитопровода с зазором,получим
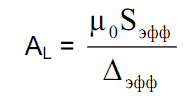
Еще более простой получается формула для максимального тока через дроссель
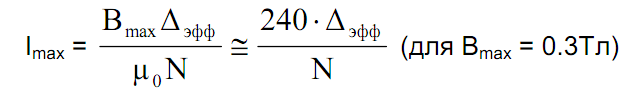
т. е. допустимый ток определяется только эффективным зазором и числом витков.
 Почти все приведенные выше формулы уже были опубликованы в журнале «Схемотехника» [4], однако ни в одной из известных автору статьи публикаций не отмечено, что эффективная ширина зазора, которую надо применять в расчетах, меньше геометрической. Это различие возникает из-за того, что магнитное поле, существующее рядом с зазором (Рис. 1), шунтирует зазор и уменьшает его эффективную ширину. Для того, чтобы рассчитать влияние этого поля, можно обратиться к аналогии между магнитным и электрическим полями. Воспользуемся формулой для емкости конденсатора из двух цилиндров с близко расположенными торцами [6]:
Почти все приведенные выше формулы уже были опубликованы в журнале «Схемотехника» [4], однако ни в одной из известных автору статьи публикаций не отмечено, что эффективная ширина зазора, которую надо применять в расчетах, меньше геометрической. Это различие возникает из-за того, что магнитное поле, существующее рядом с зазором (Рис. 1), шунтирует зазор и уменьшает его эффективную ширину. Для того, чтобы рассчитать влияние этого поля, можно обратиться к аналогии между магнитным и электрическим полями. Воспользуемся формулой для емкости конденсатора из двух цилиндров с близко расположенными торцами [6]:
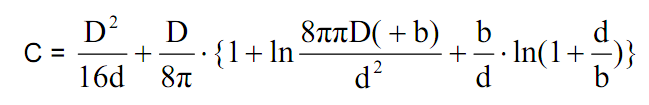
где С — емкость конденсатора в сантиметрах, D— диаметр цилиндров, b — их высота, d — зазор между их торцами.
Нетрудно заметить, что первое слагаемое соответствует емкости зазора между цилиндрами, а второе— емкости, вносимой боковыми поверхностями цилиндров. Будем считать, что высота цилиндров равна их удвоенному диаметру b = 2D. Это означает, что мы учтем только емкость ближайшей к зазору части боковой поверхности цилиндров, пренебрегая дальней. Расчеты при длине цилиндров в 3 или 4 диаметра дают практически тот же результат.
Для того, чтобы в дальнейшем перейти от емкости между цилиндрами к емкости между прямоугольными брусками (а это по форме ближе к сечению ферритового кольца), будем считать, что емкость, вносимая боковыми поверхностями, пропорциональна периметру зазора, и выразим в этой формуле диаметр цилиндров через периметр р их кругового сечения:
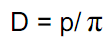
высота цилиндров b = 2D = 2р/тг.
Если в формулу для емкости подставить эти выражения, можно определить из нее отношение полной емкости к емкости между торцами в функции от отношения зазора к периметру цилиндров β = d/b. Формула эта, однако, получается довольно громоздкой и неудобной для применения.
Обозначим буквой а отношение эффективного зазора, обеспечивающего без емкости боковых поверхностей ту же емкость, что и емкость между торцами с учетом емкости боковых поверхностей, к геометрическому. На Рис. 2 приведена расчетная зависимость а от β. Из подобия уравнений, описывающих электрическое и магнитное поле, следует, что аналогично выглядит и зависимость отношения эффективного магнитного зазора к геометрическому от отношения геометрического магнитного зазора к периметру.

Из графика на Рис. 2 следует, что эффективная ширина зазора может существенно отличаться от геометрической. В реальном диапазоне β составляет от 0,01 до 0,1 эффективная ширина зазора меньше геометрической в 1,26. 2,66 раза.

В Таблице 1 приведены значения AL для кольцевых магнитопроводов с четырьмя различными зазорами, рассчитанные с учетом отличия эффективного зазора от геометрического.
Вышесказанное позволяет сделать вывод, что необходимые число витков и зазор практически не зависят от начальной магнитной проницаемости материала магнитопровода, и поэтому можно применить ферриты с любой проницаемостью, большей 600. Для любого имеющегося кольца с табличным зазором по значению AL нетрудно вычислить индуктивность или необходимое число витков и рассчитав β = Δ/р, по графику (рис. 2) определить значение а = Δэфф /р и Δэфф = ap. По найденному значению Δэфф и приведенной ранее формуле можно найти максимальный ток, не вызывающий насыщения сердечника.
Однако существует еще одно обстоятельство, влияющее на выбор магнитопровода — возможность намотки на него требуемого числа витков проводом соответствующего сечения. Необходимая площадь окна кольца составляет
Sокн = NSпров/Кзап
где Sпров — сечение провода, а kзап — коэффициент заполнения окна. Расчет Sпров производят по формуле Sпров = l/j . где j — допустимая плотность тока. Типовое значение kзап по меди составляет 0,3, а для j при начальном расчете принимают значение 2,5 А/мм2.
Подставив в формулу для расчета площади окна выражения для N и АL, получим следующую формулу:
I 2 L = (Sокнjkзап) 2 μSэфф/Δэфф
Подобное выражение можно получить и из формулы для максимального тока, который можно пропустить через дроссель без насыщения сердечника:
I 2 L = Bmax 2 Sэфф lэфф ( μ μэфф )
Однозначного расчета конструктивных параметров дросселя по заданной индуктивности и току не существует. Однако при подборе кольца и определении данных обмотки могут помочь последние восемь колонок табл. 1 . В них приведены максимальные значения произведения l 2 L по насыщению и по заполнению, рассчитанные по приведенным выше формулам для Вmах = 0,3 Тл, kзan = 0,3, j = 2,5 А/мм 2 и четырех значений зазора.
Подбор колец и расчет конструктивных параметров дросселей продемонстрируем на двух примерах.
Пусть необходим дроссель индуктивностью 22 мкГн на рабочий ток 1,2 А. Для него значение l 2 L = 1,22х22 = 31,68. Среди колец минимального диаметра первым почти подходит кольцо К10x6x4,5. При введении в него зазора 0,25 мм имеем возможность намотать дроссель с большим запасом по току (Таблица 1, колонка «нас»), но с некоторым превышением плотности тока относительно 2,5 А/мм 2 (колонка «зап.»).
Определим параметры дросселя при зазоре 0,25 мм. Для него коэффициент индуктивности по Таблице 1 составит AL = 0,064, необходимое число витков
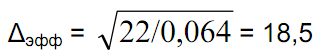
(округляем до 19), допустимый ток Для I = 1,2 А при j = 2,5 А/мм2 необходим провод сечением
Sпров = I/j = 1,2/2,5 = 0,48mm 2
При коэффициенте заполнения kзап = 0,3 необходимая площадь окна составит
Площадь окна по Таблице 1 составляет 28,3 мм 2 , что несколько меньше. Необходимо за счет увеличения плотности тока уменьшить сечение провода до
Sпров = Sокн kзап/N = 28,3×0,3/19 = 0,446 мм 2
Плотность тока составит j = I/Sпров = 1,2/0,446 = =2,68 А/мм 2 , что вполне допустимо. Диаметр провода указанного сечения (по меди) можно рассчитать по формуле:
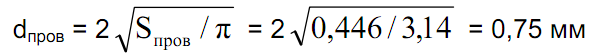
Пусть необходим дроссель 88 мкГн на ток 1,25 А. Для него l 2 L = 137,5. Дроссель можно намотать на кольце К12x6x4,5 с тем же зазором, при этом насыщения магнитопровода происходить не будет, но плотность тока существенно превысит норму. Поэтому необходимо перейти к кольцу большего размера. В распоряжении автора были кольца К12x8x3 из феррита М4000НМ. На одном кольце невозможно намотать необходимый дроссель, ни по насыщению сердечника, ни по заполнению окна. Можно сложить два кольца вместе. В этом случае эффективное сечение магнитопровода увеличивается в два раза, а допустимые значения l 2 L вырастут по насыщению несколько более, а по заполнению несколько менее, чем в два раза. Поэтому необходимый дроссель при геометрическом зазоре 0,25 мм можно намотать с запасом по току насыщения и с небольшим превышением плотности тока.
Только табличными сведениями теперь не обойтись, необходим полный расчет. Для двух колец периметр сечения (при зазоре 0,25 мм):
р = D-d+4xh = 12-8+4×3 = 16 мм,
β=Δ/р = 0,25/16 = 0,0156.
По графику на Рис. 2 находим а = 0,73, откуда эффективный зазор
Δэфф = Δа = 0,25×0,73 = 0,183 мм.
Найденное значение
AL= μSэфф/Δэфф = 1,257х10 -3 х2х5,92/0,183 = 0,081
Необходимое число витков
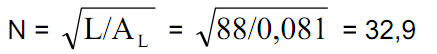
округляем в большую сторону до 33 витков. Максимальный ток через дроссель
lmax = 240 Δэфф /N = 240×0,183/33 = 1,33 А.
Максимальное сечение провода
Sпров = Sокн kзап/N = 50,3×0,3/33 = 0,457 мм 2 ,
что соответствует плотности тока 1,25/0,457 = 2,74 А/мм 2 . Сечению Sпров = 0,457 мм 2 соответствует диаметр:
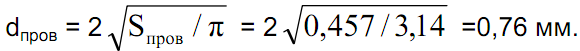
Иногда удобнее ввести два одинаковых зазора. В этом случае табличное значение AL для половинного зазора следует уменьшить в два раза, а табличное значение I 2 L для половинного зазора — удвоить.
Технология введения зазора такова. Небольшое кольцо перед намоткой разломить на две части, надпилив его надфилем, лучше алмазным. Половинки склеивают между собой эпоксидным клеем с наполнителем, в качестве которого удобно использовать тальк. При склеивании в один из зазоров или в оба на часть глубины вводят прокладку из гетинакса, текстолита или нескольких слоев бумаги. Можно считать, что толщина одного листа бумаги для ксероксов и лазерных принтеров составляет 0,1 мм. Для сохранения формы кольца в процессе полимеризации клея оно должно лежать на обрезке органического стекла, от которого затем легко отделяется при изгибе этого обрезка. Перед намоткой острые грани колец следует тщательно скруглить небольшим наждачным камнем.
У большого кольца зазор можно также выполнить ножовкой с алмазным полотном, однако его ширина при этом однозначно определяется толщиной полотна. В такой зазор для сохранения прочности кольца следует вклеить прокладку из жесткого диэлектрика.
Для экспериментальной проверки тока насыщения дросселей автором была изготовлена приставка к осциллографу, схема которой приведена на Рис. 3. Устройство представляет собой упрощенный вариант обратноходового преобразователя.

На микросхеме DD1 собран генератор импульсов положительной полярности длительностью, регулируемой в пределах 10. 300 мкс с периодом повторения около 10 мс. Импульсы с его выхода поданы на затвор мощного, но низковольтного и относительно недорогого полевого транзистора VT2. Транзистор открывается и через проверяемую катушку индуктивности L1 начинает течь линейно нарастающий ток. Когда импульс заканчивается, накопленная энергия передается через диод VD2 в нагрузку, которой служат стабилитроны VD3 и VD4. Напряжение с резистора R7, пропорциональное току через катушку L1, подается на осциллограф. Для синхронизации осциллографа лучше использовать сигнал с выхода DD1.4. Если ток превысит 6А, откроется транзистор VT1 и оборвет формирование импульса. Пока сердечник катушки не входит в насыщение, зависимость тока от времени, как указывалось выше, носит линейный характер. При плавном увеличении длительности импульсов и подходе максимального тока через дроссель к току насыщения на экране осциллографа хорошо видно резкое отклонение зависимости от линейной. Источник напряжением 20 В должен допускать выходной ток не менее 1 А. Для упрощения пользования приставкой можно цепь +6 В питать от цепи +20 В через микросхемный стабилизатор КР145ЕН5Б(Г), либо КР1157ЕН6 с любыми суффиксами (7806 или 78L06). Экспериментальная проверка изготовленных дросселей подтвердила точность расчета необходимого числа витков и тока насыщения порядка ±10 %, что можно считать неплохим результатом, учитывая ошибки установки ширины зазора и множество допущений при выводе формул
Литература:
1. И. Н. Сидоров, А. А. Христинин, С. В. Скорняков. Малогабаритные магнитопроводы и сердечники. Справочник.— М.: Радио и связь, 1989, с. .384,
2. А. Миронов. Магнитные материалы и магнитопроводы для импульсных источников питания.— Радио, 2000, №6, с. 53, 54.
3. Ферритовые магнитопроводы серии RM фирмы EPCOS. — Радио, 2001, №3, с. 49—51, №10, с. 48—50.
4. А. Кузнецов. Трансформаторы и дроссели для импульсных источников питания. — Схемотехника, 2000, №1, с. 30—33, №2, с. 48, 49, 2001, №1, с. 32—34.
5. С. Бирюков. Цифровой измеритель RCL. — Радио, 1996, №3, с. 38—41, №7, с. 62, 1997, №7, с. 32, 1998, №5, с. 63, 2001, №5, с. 44.
6. Г. Г. Гинкин. Справочник по радиотехнике. Изд. 4-е, переработанное. — М.: Госэнергоиздат, 1948, с. 816.
 Очень часто у начинающих радиолюбителей возникает необходимость рассчитать дроссель на ферритовом сердечнике для импульсного источника питания, либо для другой цепи в которой циркулируют значительные токи. При этом, погуглив по запросу «расчет индуктивности на ферритовом кольце», с большой вероятностью он попадет на наш онлайн-калькулятор. Воспользовавшись этим калькулятором или самой программой Coil32 для расчета индуктивности дросселя, радиолюбитель чаще всего приходит к результатам не совпадающим ни со справочной литературой по расчету импульсных силовых цепей, ни с реальностью ( пример обсуждения подобной ситуации на форуме ). Дело может даже закончиться выгоранием транзисторов и прочих мосфетов и проклятиями в адрес разработчиков Coil32. В чем же дело? Давайте разберемся…
Очень часто у начинающих радиолюбителей возникает необходимость рассчитать дроссель на ферритовом сердечнике для импульсного источника питания, либо для другой цепи в которой циркулируют значительные токи. При этом, погуглив по запросу «расчет индуктивности на ферритовом кольце», с большой вероятностью он попадет на наш онлайн-калькулятор. Воспользовавшись этим калькулятором или самой программой Coil32 для расчета индуктивности дросселя, радиолюбитель чаще всего приходит к результатам не совпадающим ни со справочной литературой по расчету импульсных силовых цепей, ни с реальностью ( пример обсуждения подобной ситуации на форуме ). Дело может даже закончиться выгоранием транзисторов и прочих мосфетов и проклятиями в адрес разработчиков Coil32. В чем же дело? Давайте разберемся…
Причина кроется в том, что начинающие радиолюбители часто либо не знают, либо имеют упрощенный взгляд на особенности намагничивания феррита. Вот мы взяли сердечник, засунули его в катушку и ее индуктивность возросла на величину относительной магнитной проницаемости сердечника. Верно? Верно, да не совсем! Один только факт, что для описания свойств феррита существует несколько магнитных проницаемостей, говорит, что не все так однозначно. Магнитные свойства феррита наиболее полно описываются семейством так называемых кривых намагничивания, иначе называемых «петля гистерезиса».  Как происходит процесс намагничивания/размагничивания феррита, что такое остаточная индукция Br, коэрцитивная сила Hc, индукция насыщения, предельная петля гистерезиса [1] и т.д. уже достаточно подробно описано и вы можете прочитать об этом по ссылкам в конце статьи. Мы же остановимся здесь на том, как меняется магнитная проницаемость сердечника в процессе его перемагничивания, поскольку этот параметр использует для расчетов Coil32. Вот неполный список понятий магнитной проницаемости в котором начинающему радиолюбителю не грех и запутаться:
Как происходит процесс намагничивания/размагничивания феррита, что такое остаточная индукция Br, коэрцитивная сила Hc, индукция насыщения, предельная петля гистерезиса [1] и т.д. уже достаточно подробно описано и вы можете прочитать об этом по ссылкам в конце статьи. Мы же остановимся здесь на том, как меняется магнитная проницаемость сердечника в процессе его перемагничивания, поскольку этот параметр использует для расчетов Coil32. Вот неполный список понятий магнитной проницаемости в котором начинающему радиолюбителю не грех и запутаться:
- Относительная и абсолютная магнитная проницаемость. По сути различаются только множителем µ = 4π*10 -7 ., который реально согласует в системе СИ единицы измерения в электромагнетизме и единицы длины и условно именуется как магнитная проницаемость вакуума или магнитная постоянная.
- В общем случае величина относительной магнитной проницаемости пропорциональна наклону касательной к кривой намагничивания в данной точке. Эта величина называется дифференциальной магнитной проницаемостью. Она не постоянна и динамически меняется при движении по кривой намагничивания.
- Начальная магнитная проницаемость µi характеризуется наклоном начальной кривой намагничивания [0] в начале координат. Обычно эта величина приводится в справочниках.
- Максимальная магнитная проницаемость µmax. При намагничивании феррита его магнитная проницаемость растет, достигая некоторого максимума, а затем начинает уменьшаться. Величина максимальной магнитной проницаемости обычно в разы больше начальной. Также можно найти в справочниках по ферритам.
- Динамическая магнитная проницаемость. Характеризует насколько возрастет индуктивное сопротивление переменному току у катушки, если воздух вокруг нее заменить на наш феррит. Т.е. как раз то, что нас интересует. Если феррит помещен в относительно слабое переменное магнитное поле, не загоняющее его в предельную петлю гистерезиса, то его петлю перемагничивания (частную петлю гистерезиса) можно приближенно представить как эллипс. Тогда с достаточным приближением можно считать, что динамическая магнитная проницаемость характеризуется наклоном большой оси этого эллипса.
- Эффективная магнитная проницаемость. Это величина относится не к самому ферриту, а к сердечнику из него с разомкнутой магнитной цепью.
При слабых полях, без подмагничивания постоянным током (важно!), феррит перемагничивается условно по кривой [3] и в этом случае величина динамической магнитной проницаемости близка к величине начальной магнитной проницаемости феррита. Поэтому в слаботочных цепях с относительно небольшой погрешностью при расчетах можно использовать величину начальной магнитной проницаемости, что и делает наш онлайн калькулятор и программа Coil32.
Другое дело силовой дроссель в импульсной схеме питания. Ферриты широкого применения имеют относительно низкое значение индукции насыщения (около 0.3Т), поэтому в цепи силового ключа дроссель переключается между максимальным значением поля, когда он почти заходит в режим насыщения и нулевым значением поля, когда он размагничивается до величины остаточной индукции (кривая [4]). Как мы видим наклон большой оси эллипса 4 намного меньше чем у эллипса 3. Другими словами магнитная проницаемость сердечника в таком режиме значительно снижается. Ситуация усугубляется если сердечник дросселя кроме того подмагничивается постоянным током (кривая [5]). Предельная петля гистерезиса реального феррита более прямоугольна, чем на нашем схематическом рисунке и, в итоге, динамическая магнитная проницаемость силового дросселя на ферритовом кольце падает до единиц. Будто бы феррита и нет совсем! В итоге, индуктивное сопротивление дросселя падает, ток резко возрастает (что ведет еще к большему уменьшению µ!), ключевой транзистор греется и выходит из строя. А расчеты из Coil32 для такого дросселя дают абсолютно неверный результат. Ведь мы использовали при расчете начальную магнитную проницаемость, а в реальной схеме она на два-три порядка меньше. В такую же ситуацию вы попадете, если измерите относительную магнитную проницаемость кольца методом пробной намотки, ведь прибор, измеряющий индуктивность, также является слаботочным устройством.
Выходом из ситуации является использование ферритового сердечника с разорванной магнитной цепью. В случае ферритового кольца, его приходится ломать пополам и потом склеивать с зазором. Предельная петля гистерезиса такого сердечника становится более пологой [2], остаточная индукция значительно меньше [B’r], эффективная магнитная проницаемость тоже меньше, чем у сердечника без зазора. Однако при этом, кривая перемагничивания [6] показывает, что динамическая магнитная проницаемость у такого дросселя намного выше, чем у аналогичного, но с сердечником без зазора. Реально она имеет величину порядка 50..100 и слабо зависит от величины начальной магнитной проницаемости феррита. Coil32 такой дроссель также не в состоянии правильно рассчитать, поскольку не учитывает немагнитный зазор. Другим выходом из ситуации является применение специальных колец для силовых дросселей из распыленного железа, Iron Powder (это не феррит). Именно такие кольца можно найти в импульсных блоках питания и на материнских платах компьютеров. «Зазор» в таком кольце как бы размазан по всему его объему.
Вывод. Программа Coil32 рассчитывает только слаботочные катушки на ферритовых кольцах, работающие в слабых полях. Для расчета силовых дросселей необходимо применять совершенно другую методику, в чем вам могут помочь следующие ссылки:
- КАК ЖЕ РАБОТАЮТ ТРАНСФОРМАТОРЫ И ДРОССЕЛИ – физические законы по которым работают трансформаторы и дроссели, петля гистерезиса, основные формулы.
- Трансформаторы и дроссели для ИИП – формулы и таблицы для расчета дросселей и трансформаторов импульсных источников питания.
- Сердечники из распылённого железа (IronPowder) – таблицы параметров сердечников из порошкового железа.
- Дроссели для импульсных источников питания на ферритовых кольцах – таблицы и формулы для расчета дросселя на кольце из феррита широкого применения.
- РАСЧЁТ ДРОССЕЛЯ – В.Я. Володин. Изложена оригинальная методика расчетов силовых дросселей как на стальных, так и на ферритовых сердечниках. Приведены формулы расчетов и примеры.
- Силовая электроника для любителей и профессионалов Б.Ю. Семенов 2001 – Доступным языком рассказывается о проектировании импульсных устройств питания. (Выбор магнитных материалов, расчет дросселей и трансформаторов, "Зачем нужен этот зазор?", MOSFET, IGBT, чоппер, бустер и т.п.) Практические примеры конструкций и расчетов.
- Параметры ферритов широкого применения – справочная таблица основных характеристик.
