Делаю тут проект и возникла вот какая проблема. Получаю данные с АЦП (дельта-сигма) микросхемы в которую встроен контроллер и фильтр, но этот фильтр имеет довольно убогую АЧХ, в итоге идёт завал по ВЧ от 60Гц и далее. Выглядит это примерно так:

Т.е. такая неравномерность АЧХ нас явно не устраивает (не проходит по техническим требованиям), правда есть возможность повысить частоту дискретизации с 250Гц до 500Гц, чтобы выровнять АЧХ, однако тогда увеличивается объём данных который ещё нужно будет усреднять, что скажется на производительности (проект на STM32F103VE) системы в целом и на общем потреблении энергии (батарейное питание). Но есть и другой путь.
Можно выровнять АЧХ с помощью параметрического цифрового фильтра, в данном случае ВЧ. То есть это тоже самое что эквалайзер, мы поднимаем одни частоты, а другие не трогаем (или заваливаем). Такой метод конечно хорош, но т.к. мы пытаемся восстановить информацию, часть которой была уничтожена другим фильтром на входе (тот что в микросхеме), неизбежно увеличится уровень помех на высоких частотах, т.к. вместе с сигналом мы усилим также и их, но вот насколько?
Итак, идея решения проблемы есть, осталась реализация. Что мы помним о цифровых фильтрах (к тем кто не имел с ними практики) из университетского курса? Разве что такие слова как свёртка, Z-преобразование, импульсная характеристика и т.д. В общем не понятно с какого конца подходить даже, вроде надо какие-то коэффициенты рассчитывать, но что и зачем непонятно, поднимать курс и сидеть с книгами по ЦОС (есть одна на 800 страниц) нет времени, проект стоит и надо что-то делать, и быстро.
Поэтому немного погуглив находим вот такой ресурс в интернете. Это сайт по расчёту цифровых фильтров (и не только!) он-лайн, а сделал его некий Dr Anthony J. Fisher.
Итак задаёмся требованиями которые нам нужны и вводим на сайте. Во-первых, нам нужна плавная характеристика, поэтому однозначно Баттерворт первого порядка ВЧ (highpass). Во-вторых, sample rate, т.е. количество преобразований АЦП в секунду, или частота дискретизации, у нас это 250Гц. Вводим. И наконец, в-третьих, частота среза (-3дБ) — 50Гц, т.к. фильтр на входе режет примерно здесь. Нажимаем отправить и получаем вот такую характеристику нашего будущего фильтра:

Красным представлен график амплитуды от частоты Найквиста, синим изменение фазы. 0,5 соответствует половине частоты дискретизации.
Также получаем С код с рассчитанными коэффициентами:
Но это только фильтр, помним, что нам нужно усилить частоты от 50Гц и выше, чтобы выпрямить АЧХ, и эта функция в таком виде нам не поможет, поэтому путём нехитрых манипуляций приводим функцию к такому виду:
Всё. Чтобы использовать фильтр кидаем данные в параметры функции, а возвращает она отфильтрованные данные. Коэффициент усиления OUR_GAIN подбираем опытным путём, снимая показания с АЦП и замеряя АЧХ.
Таким образом мне удалось поднять АЧХ практически без дополнительной нагрузки на контроллер и мой проект прошёл по техническим требованиям (в медицинской области они весьма не хилые). Я боялся, что сильно возрастёт уровень помех, но он увеличился с 4-5мкВ примерно до 6-8мкВ, что нас устраивает. В заключении могу порекомендовать ещё одну бесплатную программу по расчёту цифровых фильтров — WinFilter, скачать её можно здесь. Насколько она работоспособна не знаю, не проверял, но она может выдавать код в VHDL (и в С естественно), что наверняка пригодится для ПЛИС. Также есть программа от Texas Instuments, по расчёту коэффициентов цифровых фильтров, называется она TIBQ. Всё. Удачи в проектировании цифровых фильтров.
Меню Фильтры содержит функции, накладывающие различные фильтры:
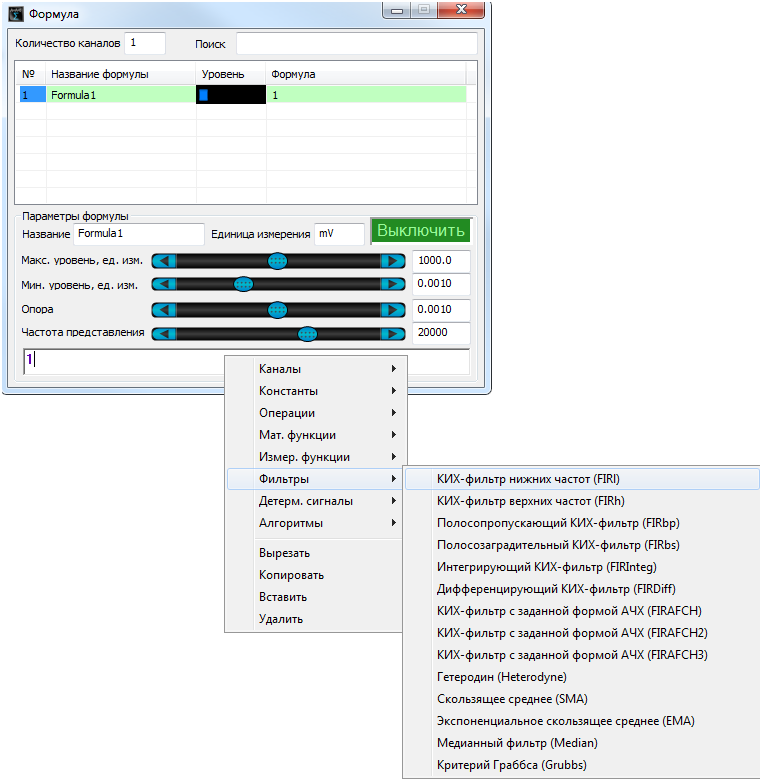
Несколько слов насчет использования КИХ-фильтров
Фильтры с конечной импульсной характеристикой (КИХ-фильтры) имеют задержку, определяемую количеством коэффициентов. Причем задержка всегда равна количеству коэффициентов фильтра. Также количество коэффициентов служит мерой точности фильтра: отношение частоты дискретизации по каналу, отнесенное к числу коэффициентов фильтра представляет собой половину полосы частот в которой фильтр удовлетворяет требованиям. Вообще говоря, для цифрового фильтра в подавляющем числе случаев число коэффициентов лучше увеличивать. Но есть одно важное ограничение: при большом числе коэффициентов фильтрация сигнала занимает слишком много процессорного времени. В связи с этим в программе Формула введен алгоритм вычисления оптимального числа коэффициентов.
Количество коэффициентов фильтра вычисляется согласно следующему алгоритму:
1) определяется тактовая частота установленного процессора, и число коэффициентов рассчитывается так, чтобы загрузка одного ядра процессора составляла 3%. Формула для расчета:
где tapslen — число коэффициентов фильтра,
CPUSPEED — тактовая частота процессора, Гц,
ADC_FREQUENCY — частота дискретизации по фильтруемому каналу.
2) Если полученный результат превышает рационально допустимое количество коэффициентов (2000), то количество коэффициентов приравнивается к нему.
3) Если полученный результат меньше минимально допустимого(20), то количество коэффициентов приравнивается к нему.
4) Если полученный результат не позволяет вычислить результат с требуемой точностью по частоте, то используется формула:
где NORM_FREQ — нормализованная частота, т.е. введенная частота отнесенная к частоте дискретизации.
5) Если же полученный результат является слишком дорогостоящим по вычислительной мощности (загружает более 30% одного ядра процессора), то окончательный результат будет рассчитываться по формуле:
Пусть необходимо рассчитать временную задержку по каналу с частотой дискретизации 500 кГц на двухядерном процессоре 2.5 ГГц, при наложении ФНЧ на 300 Гц.
Воспользуемся алгоритмом по шагам:
1) tapslen = 2.5e+9 * 2e-2 / 5e+5 = 100 — вариант при котором загрузка процессора составит 2% делённое на количество ядер, т.е. 1%
2), 3) — не влияют на результат
4) tapslen = 1 / (5e-1 * 3e+2 / 5e+5) = 3.3e+3 — такое количество коэффициентов необходимо для удовлетворения поставленной задачи
5) tapslen = 2.5e+9 * 3e-1/ 5e+5 = 1500 — такое количество коэффициентов мы можем себе позволить при данных условиях.
Теперь, когда получено количество коэффициентов фильтра tapslen = 1500, оценим временную задержку и то насколько требуемый фильтр удовлетворяет нашим требованиям по точности.
Временная задержка dt = tapslen/ADC_FREQUENCY = 1.5e+2 / 5e+5 = 3e-4 (секунды), или 300 мкс.
Частота среза фильтра составит: Fсреза = ADC_FREQUENCY/(0.5e-1 * tapslen) = 5e+5 / ( 0.5e-1 * 1.5e+3) = 6.7e+3 (Герц), т.е. в два раза больше чем требовалось.
Будьте внимательны! При высоких частотах дискретизации не стоит настраивать фильтры с очень большой точностью — вы загрузите процессор, а результата так и не добьетесь. Старайтесь выбирать для измерений наиболее оптимальный диапазон частот. Если вам нужно исследовать ВЧ-сигнал, то мы советуем использовать аппаратный гетеродин.
Примечание: в программе Фильтрация сигналов используются фильтры с бесконечной импульсной характеристикой. При описании фильтров Формулы будут приводиться результаты работы фильтров программы Фильтрация сигналов — для сравнения.
Описание фильтров
FIRl( , const) – фильтр низких частот с граничной частотой равной const. Частота не может быть меньше нуля и больше половины частоты дискретизации. Данный тип фильтра следует использовать для отсечения нежелательных высокочастотных составляющих, к примеру — в задаче идентификации движения человека или автомобиля по земле, где интересующий нас сигнал лежит в области низких частот.
FIRh( , const) – фильтр высоких частот с граничной частотой равной const. Частота не может быть меньше нуля и больше половины частоты дискретизации. Данный тип фильтра следует использовать для отсечения постоянной и низкочастотной составляющих сигнала. Пример использования: вывод звуковой информации с отсечением неслышимой части и постоянной составляющей.
На рисунках ниже приведен пример фильтрации шумового сигнала (используется функция формулы ) фильтром низких и фильтром высоких частот в программе Формула и программе Фильтрация сигналов.
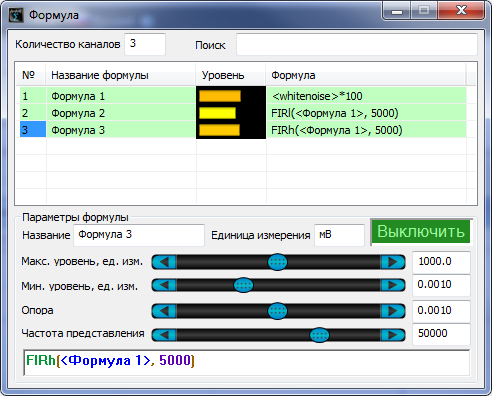
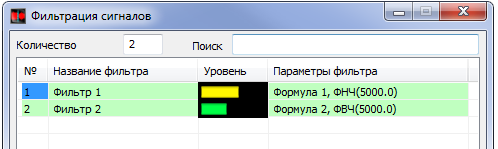

Спектр исходного сигнала
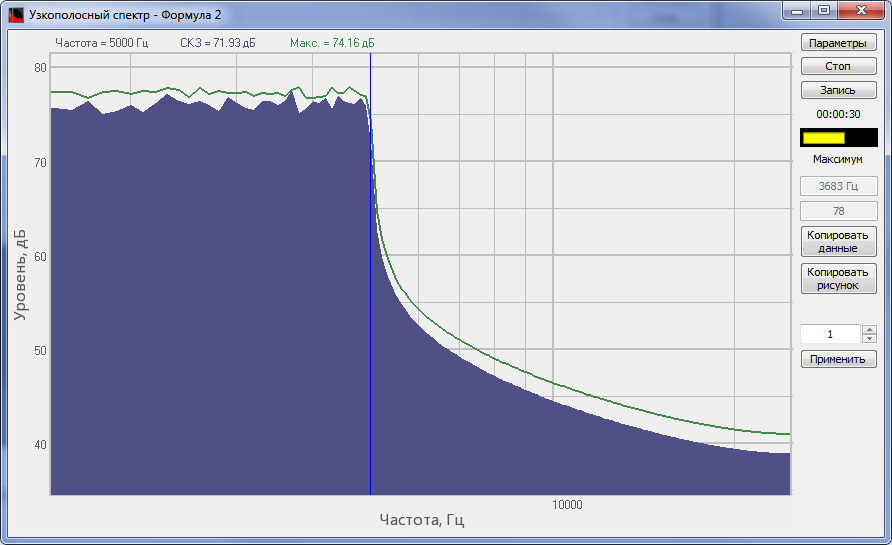
Спектр сигнала, обработанного ФНЧ программы Формула
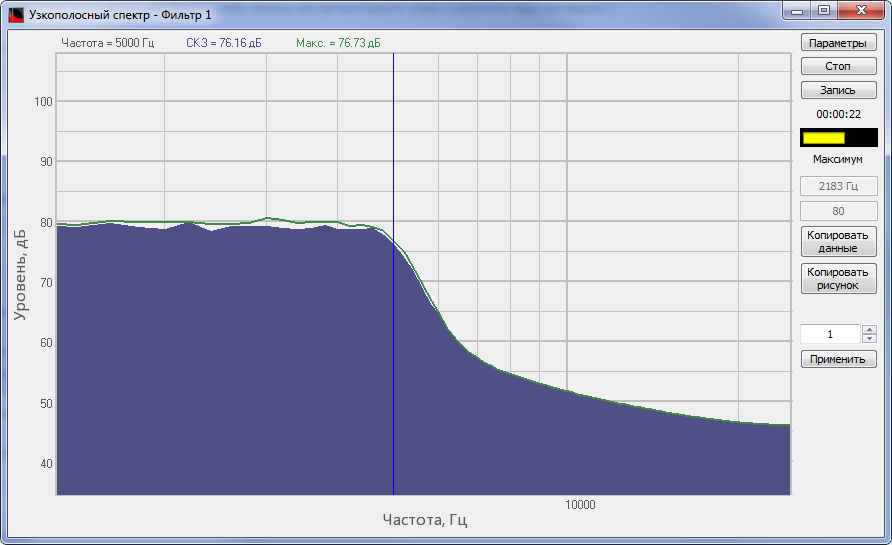
Спектр сигнала, обработанного ФНЧ программы Фильтрация сигналов
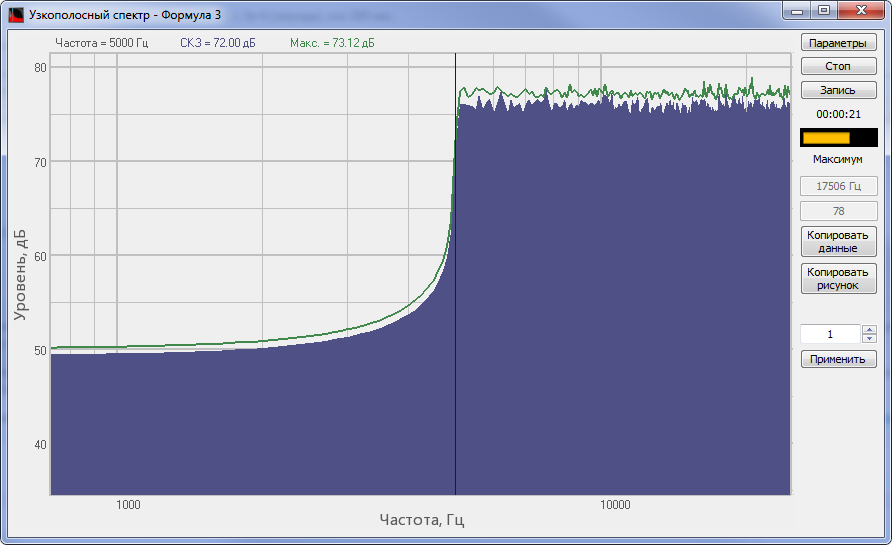
Спектр сигнала, обработанного ФВЧ программы Формула
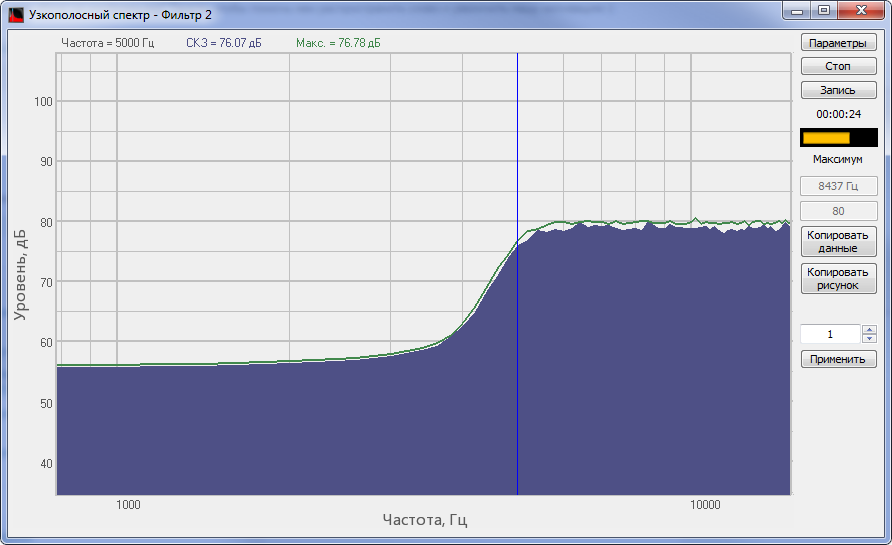
Спектр сигнала, обработанного ФВЧ программы Фильтрация сигналов
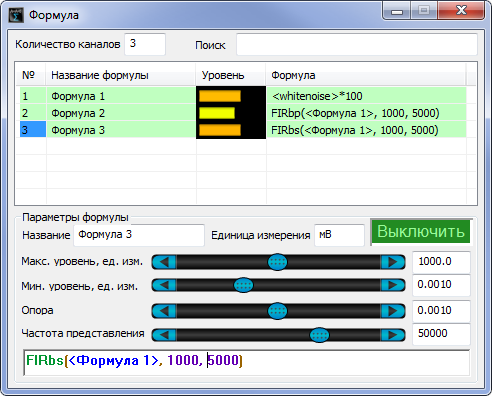
FIRbp( , const 1, const 2) – полосовой фильтр, пропускающий частоты от первой до второй. Значения частот не могу быть меньше нуля и больше половины частоты дискретизации. Если введены такие значения, то фильтр на их место подставляет предельно допустимые. Фильтр может быть использован для вырезания частот соответствующих человеческому голосу.
FIRbs( , const 1, const 2) – полосовой фильтр, вырезающий частоты от первой до второй. Значения частот не могу быть меньше нуля и больше половины частоты дискретизации. Если введены такие значения, то фильтр на их место подставляет предельно допустимые. Разницы в порядке следования частот в выражении нет.
На рисунках ниже приведен пример фильтрации шумового сигнала (используется функция формулы ) полосопропускающим фильтром (ППФ) и полосозаграждающим фильтром (ПЗФ) в программе Формула и программе Фильтрация сигналов.
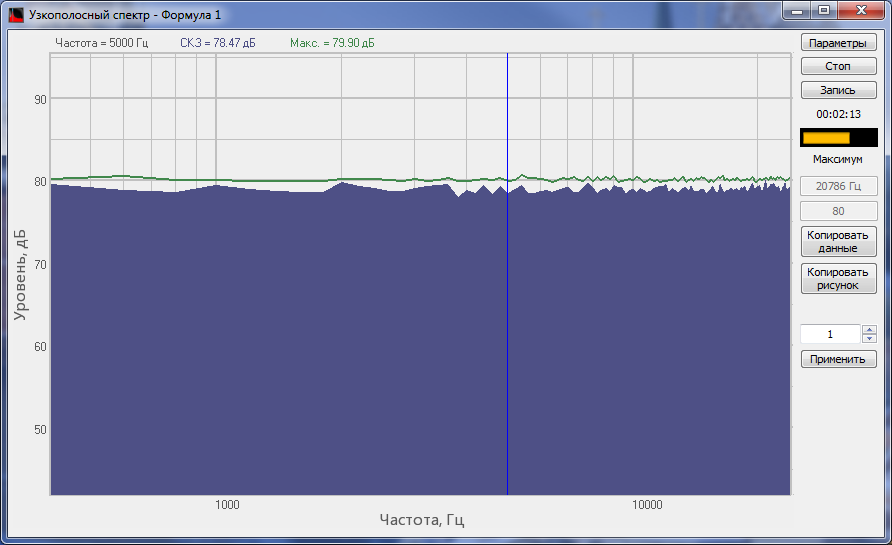
Спектр исходного сигнала
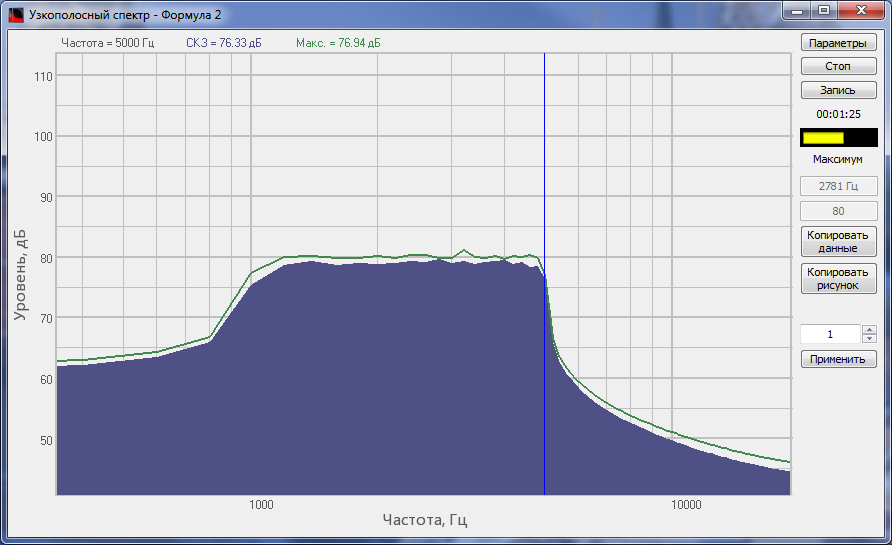
Спектр сигнала, обработанного ППФ программы Формула
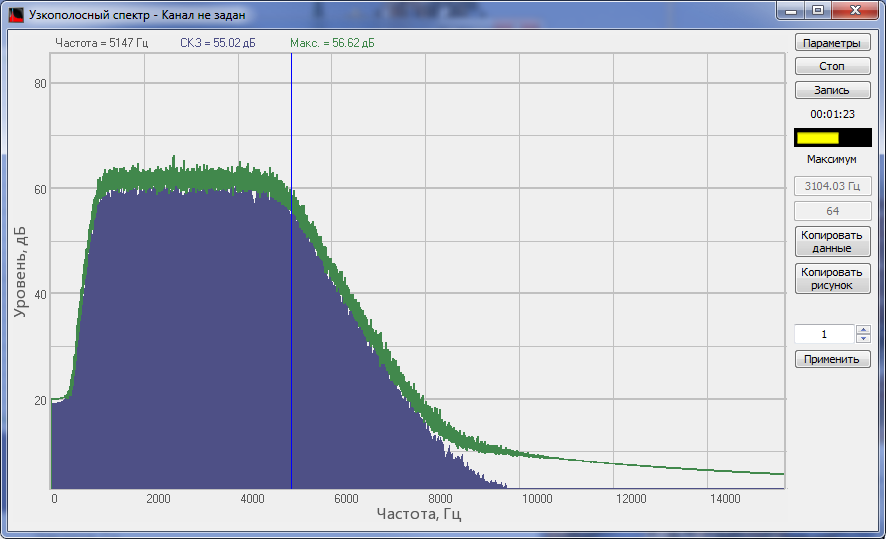
Спектр сигнала, обработанного ППФ программы Фильтрация сигналов
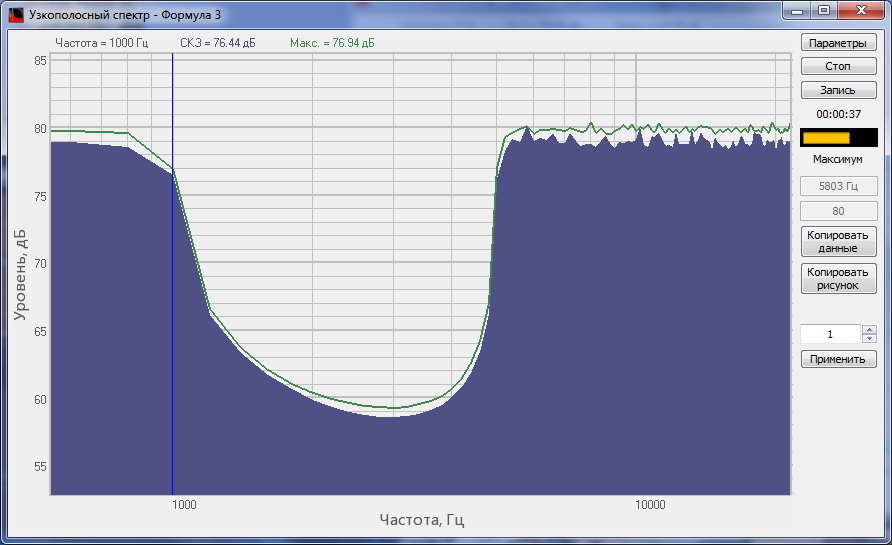
Спектр сигнала, обработанного ПЗФ программы Формула
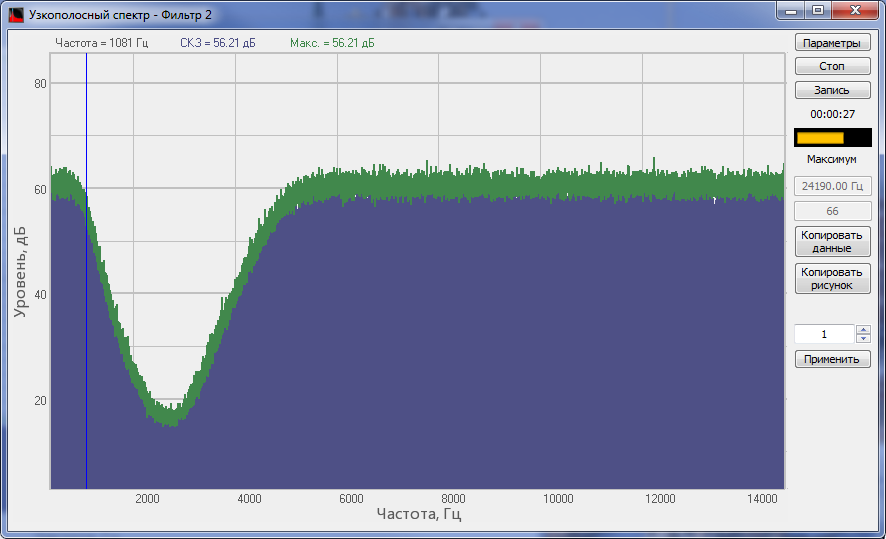
Спектр сигнала, обработанного ПЗФ программы Фильтрация сигналов
FIRInteg( ) – интегрирующий КИХ-фильтр, является потенциально неустойчивым, поэтому перед его применением следует ставить фильтр высоких частот.
FIRDiff( ) — дифференцирующий КИХ-фильтр
FIRAFCH( , ) – КИХ-фильтр с заданной формой АЧХ.
Heterodyne( , частота, полоса) – гетеродин. Вырезает из спектра сигнала полосу с частотой Frequency Гц и полосой Band Гц. Затем сдвигает её в область низких частот. Основным использованием гетеродина является частотная демодуляция сигнала — процесс переноса части спектра из области высоких частот в область низких. Применяется в радиотехнических задачах.
SMA( , время) — фильтрует скользящее среднее значения которых в каждой точке определения равны среднему значению исходной функции за предыдущий период. Скользящие средние обычно используются с данными временных рядов для сглаживания краткосрочных колебаний. Математически скользящее среднее является одним из видов свёртки, и поэтому его можно рассматривать как фильтр низких частот, используемых в обработке сигналов. Так как при расчёте скользящего среднего значение функции вычисляется каждый раз заново, при этом учитывается конечное значимое множество предыдущих значений скользящее среднее «перемещается» (движется), как бы «скользя» по временному ряду (Подробнее).
EMA( , константа) — фильтрует экспоненциальное среднее. В обычном экспоненциальном скользящем среднем сглаживанию подвергается значения исходной функции, однако, сглаживанию могут подвергаться и значения результирующей функции. Значение «Константа» должно изменяться от 0 до 1, чем оно меньше, тем более крупным становится экспоненциальное значение (Подробнее).
Median( , Time) — эффективная процедура обработки сигналов, подверженных воздействию импульсных помех. Является одним из видов цифровых фильтров, широко используемый в цифровой обработке сигналов и изображений для уменьшения уровня шума. Медианный фильтр является нелинейным КИХ-фильтром.Значения отсчётов внутри окна фильтра сортируются в порядке возрастания (убывания); и значение, находящееся в середине упорядоченного списка, поступает на выход фильтра. В случае четного числа отсчетов в окне выходное значение фильтра равно среднему значению двух отсчетов в середине упорядоченного списка. Окно перемещается вдоль фильтруемого сигнала и вычисления повторяются (Подробнее).
Grubbs( , Time, Q) — осуществляет исключение грубых погрешностей. Для исключения грубых погрешностей используют критерий Граббса. Статистический критерий Граббса исключения грубых погрешностей основан на предположении о том, что группа результатов измерений принадлежит нормальному распределению (Подробнее). Выполнен по ГОСТ Р 8.736-2011 «ГСИ. Измерения прямые многократные. Методы обработки результатов измерений».
Меню Фильтры содержит функции, накладывающие различные фильтры:

Несколько слов насчет использования КИХ-фильтров
Фильтры с конечной импульсной характеристикой (КИХ-фильтры) имеют задержку, определяемую количеством коэффициентов. Причем задержка всегда равна количеству коэффициентов фильтра. Также количество коэффициентов служит мерой точности фильтра: отношение частоты дискретизации по каналу, отнесенное к числу коэффициентов фильтра представляет собой половину полосы частот в которой фильтр удовлетворяет требованиям. Вообще говоря, для цифрового фильтра в подавляющем числе случаев число коэффициентов лучше увеличивать. Но есть одно важное ограничение: при большом числе коэффициентов фильтрация сигнала занимает слишком много процессорного времени. В связи с этим в программе Формула введен алгоритм вычисления оптимального числа коэффициентов.
Количество коэффициентов фильтра вычисляется согласно следующему алгоритму:
1) определяется тактовая частота установленного процессора, и число коэффициентов рассчитывается так, чтобы загрузка одного ядра процессора составляла 3%. Формула для расчета:
где tapslen — число коэффициентов фильтра,
CPUSPEED — тактовая частота процессора, Гц,
ADC_FREQUENCY — частота дискретизации по фильтруемому каналу.
2) Если полученный результат превышает рационально допустимое количество коэффициентов (2000), то количество коэффициентов приравнивается к нему.
3) Если полученный результат меньше минимально допустимого(20), то количество коэффициентов приравнивается к нему.
4) Если полученный результат не позволяет вычислить результат с требуемой точностью по частоте, то используется формула:
где NORM_FREQ — нормализованная частота, т.е. введенная частота отнесенная к частоте дискретизации.
5) Если же полученный результат является слишком дорогостоящим по вычислительной мощности (загружает более 30% одного ядра процессора), то окончательный результат будет рассчитываться по формуле:
Пусть необходимо рассчитать временную задержку по каналу с частотой дискретизации 500 кГц на двухядерном процессоре 2.5 ГГц, при наложении ФНЧ на 300 Гц.
Воспользуемся алгоритмом по шагам:
1) tapslen = 2.5e+9 * 2e-2 / 5e+5 = 100 — вариант при котором загрузка процессора составит 2% делённое на количество ядер, т.е. 1%
2), 3) — не влияют на результат
4) tapslen = 1 / (5e-1 * 3e+2 / 5e+5) = 3.3e+3 — такое количество коэффициентов необходимо для удовлетворения поставленной задачи
5) tapslen = 2.5e+9 * 3e-1/ 5e+5 = 1500 — такое количество коэффициентов мы можем себе позволить при данных условиях.
Теперь, когда получено количество коэффициентов фильтра tapslen = 1500, оценим временную задержку и то насколько требуемый фильтр удовлетворяет нашим требованиям по точности.
Временная задержка dt = tapslen/ADC_FREQUENCY = 1.5e+2 / 5e+5 = 3e-4 (секунды), или 300 мкс.
Частота среза фильтра составит: Fсреза = ADC_FREQUENCY/(0.5e-1 * tapslen) = 5e+5 / ( 0.5e-1 * 1.5e+3) = 6.7e+3 (Герц), т.е. в два раза больше чем требовалось.
Будьте внимательны! При высоких частотах дискретизации не стоит настраивать фильтры с очень большой точностью — вы загрузите процессор, а результата так и не добьетесь. Старайтесь выбирать для измерений наиболее оптимальный диапазон частот. Если вам нужно исследовать ВЧ-сигнал, то мы советуем использовать аппаратный гетеродин.
Примечание: в программе Фильтрация сигналов используются фильтры с бесконечной импульсной характеристикой. При описании фильтров Формулы будут приводиться результаты работы фильтров программы Фильтрация сигналов — для сравнения.
Описание фильтров
FIRl( , const) – фильтр низких частот с граничной частотой равной const. Частота не может быть меньше нуля и больше половины частоты дискретизации. Данный тип фильтра следует использовать для отсечения нежелательных высокочастотных составляющих, к примеру — в задаче идентификации движения человека или автомобиля по земле, где интересующий нас сигнал лежит в области низких частот.
FIRh( , const) – фильтр высоких частот с граничной частотой равной const. Частота не может быть меньше нуля и больше половины частоты дискретизации. Данный тип фильтра следует использовать для отсечения постоянной и низкочастотной составляющих сигнала. Пример использования: вывод звуковой информации с отсечением неслышимой части и постоянной составляющей.
На рисунках ниже приведен пример фильтрации шумового сигнала (используется функция формулы ) фильтром низких и фильтром высоких частот в программе Формула и программе Фильтрация сигналов.



Спектр исходного сигнала

Спектр сигнала, обработанного ФНЧ программы Формула

Спектр сигнала, обработанного ФНЧ программы Фильтрация сигналов

Спектр сигнала, обработанного ФВЧ программы Формула

Спектр сигнала, обработанного ФВЧ программы Фильтрация сигналов
FIRbp( , const 1, const 2) – полосовой фильтр, пропускающий частоты от первой до второй. Значения частот не могу быть меньше нуля и больше половины частоты дискретизации. Если введены такие значения, то фильтр на их место подставляет предельно допустимые. Фильтр может быть использован для вырезания частот соответствующих человеческому голосу.
FIRbs( , const 1, const 2) – полосовой фильтр, вырезающий частоты от первой до второй. Значения частот не могу быть меньше нуля и больше половины частоты дискретизации. Если введены такие значения, то фильтр на их место подставляет предельно допустимые. Разницы в порядке следования частот в выражении нет.
На рисунках ниже приведен пример фильтрации шумового сигнала (используется функция формулы ) полосопропускающим фильтром (ППФ) и полосозаграждающим фильтром (ПЗФ) в программе Формула и программе Фильтрация сигналов.



Спектр исходного сигнала

Спектр сигнала, обработанного ППФ программы Формула

Спектр сигнала, обработанного ППФ программы Фильтрация сигналов

Спектр сигнала, обработанного ПЗФ программы Формула

Спектр сигнала, обработанного ПЗФ программы Фильтрация сигналов
FIRInteg( ) – интегрирующий КИХ-фильтр, является потенциально неустойчивым, поэтому перед его применением следует ставить фильтр высоких частот.
FIRDiff( ) — дифференцирующий КИХ-фильтр
FIRAFCH( , ) – КИХ-фильтр с заданной формой АЧХ.
Heterodyne( , частота, полоса) – гетеродин. Вырезает из спектра сигнала полосу с частотой Frequency Гц и полосой Band Гц. Затем сдвигает её в область низких частот. Основным использованием гетеродина является частотная демодуляция сигнала — процесс переноса части спектра из области высоких частот в область низких. Применяется в радиотехнических задачах.
SMA( , время) — фильтрует скользящее среднее значения которых в каждой точке определения равны среднему значению исходной функции за предыдущий период. Скользящие средние обычно используются с данными временных рядов для сглаживания краткосрочных колебаний. Математически скользящее среднее является одним из видов свёртки, и поэтому его можно рассматривать как фильтр низких частот, используемых в обработке сигналов. Так как при расчёте скользящего среднего значение функции вычисляется каждый раз заново, при этом учитывается конечное значимое множество предыдущих значений скользящее среднее «перемещается» (движется), как бы «скользя» по временному ряду (Подробнее).
EMA( , константа) — фильтрует экспоненциальное среднее. В обычном экспоненциальном скользящем среднем сглаживанию подвергается значения исходной функции, однако, сглаживанию могут подвергаться и значения результирующей функции. Значение «Константа» должно изменяться от 0 до 1, чем оно меньше, тем более крупным становится экспоненциальное значение (Подробнее).
Median( , Time) — эффективная процедура обработки сигналов, подверженных воздействию импульсных помех. Является одним из видов цифровых фильтров, широко используемый в цифровой обработке сигналов и изображений для уменьшения уровня шума. Медианный фильтр является нелинейным КИХ-фильтром.Значения отсчётов внутри окна фильтра сортируются в порядке возрастания (убывания); и значение, находящееся в середине упорядоченного списка, поступает на выход фильтра. В случае четного числа отсчетов в окне выходное значение фильтра равно среднему значению двух отсчетов в середине упорядоченного списка. Окно перемещается вдоль фильтруемого сигнала и вычисления повторяются (Подробнее).
Grubbs( , Time, Q) — осуществляет исключение грубых погрешностей. Для исключения грубых погрешностей используют критерий Граббса. Статистический критерий Граббса исключения грубых погрешностей основан на предположении о том, что группа результатов измерений принадлежит нормальному распределению (Подробнее). Выполнен по ГОСТ Р 8.736-2011 «ГСИ. Измерения прямые многократные. Методы обработки результатов измерений».
