Что ты хочешь узнать?
Ответ
Проверено экспертом


- Комментарии
- Отметить нарушение
Ответ
Функция периодическая с периодом . Область определения функции – вся числовая ось.
Область значений функции:
План построения графика. Строим сначала график функции затем растягиваем от оси Ох на 3 единицы и параллельно сдвигаем вниз на 2 единицы.
Тема: Циклические алгоритмы. Построение графиков функций.
Цели:
- Учебные:
- дать понятие возможности построения графиков функций;
- научить учащихся строить графики тригонометрических функций и с их помощью показывать свойства соответствующих функций.
-
Воспитательная:
- способствовать развитию таких мыслительных операций, как анализ, синтез, обобщение.
- Знать графики и свойства элементарных тригонометрических функций.
- Уметь читать свойства тригонометрических функций по их графикам.
Основные знания и умения:
1. Проверка домашнего задания
2. Актуализация знаний и умений
Повторить свойства тригонометрических функций.
3. Объяснение нового материала
При построении графиков функций необходимо учитывать особенности графического экрана: разрешение; ориентацию экранной системы координат.
Расчет построения графика заключается в следующем: пусть на [a; b] надо построить график функции f(х). Отрезок [a; b] ––> [0; 640] с коэффициентом k = 640/( b – а), где х = – k * а.
Точечный график можно реализовать фрагментом:
100 for x = a to b step 640/(b – a)
110 pset ( x + x + k, y – k * f(x))
120 next
Задача 1
Провести ось через центр экрана и построить график функции y = sin x.
10 screen 2
20 line (350, 0) – (350, 260)
30 line (0, 120) – (640, 120)
40 for x = 0 to 100
50 pset (10 * x, 120 + 120 * sin(x – 120) / 10)
60 next x
Рассмотренный график представляет собой совокупность точек, между которыми могут быть достаточно большие промежутки. Этот недостаток можно исправить применяя прием уплотнения:
40 for x = 0 to 100 step 0.01
Для построения более сложных графиков удобно пользоваться оператором определения функции (функция пользователя).
Задача 2
Построить график функции y = 3cosx и проверить соответствует ли он графику функции построенному с помощью программы BASIC.
Построим график функции y = cosx.
а) Область определения – множество всех действительных чисел.
б) Множество значений – отрезок [–1, 1].
в) Функция четная: cos(–x) = cosx для всех х 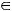 R.
R.
г) Функция периодическая с наименьшим положительным периодом 2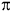 , т.е. cos(x + 2
, т.е. cos(x + 2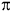 ) = cosx для всех х
) = cosx для всех х 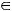 R.
R.
д) cosx = 0 при х = 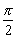 +
+ 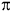 k, k
k, k 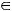 Z.
Z.
е) cosx >0 для всех х 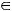 (–
(– 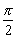 + 2
+ 2 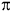 k;
k; 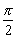 + 2
+ 2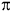 k), k
k), k 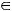 Z.
Z.
ж) cosx 0 для всех х 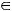 (2
(2 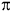 k;
k; 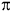 + 2
+ 2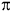 k), k
k), k 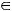 Z.
Z.
ж) sin x 0 для всех х 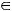 (–
(–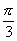 + 2
+ 2 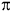 k;
k; 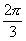 + 2
+ 2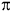 k), k
k), k 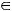 Z.
Z.
Решение
График функции пересекает ось X при f = 0
значит надо решить уравнение:
$$- 3 cos
Решаем это уравнение
Точки пересечения с осью X:
Аналитическое решение
$$x_ <1>= – operatorname
ight )> + 2 pi$$
$$x_ <2>= operatorname
ight )>$$
Численное решение
$$x_ <1>= 52.1761156937$$
$$x_ <2>= 35.7884786068$$
$$x_ <3>= 71.0256716152$$
$$x_ <4>= -83.5920422296$$
$$x_ <5>= 67.2044051427$$
$$x_ <6>= -96.1584128439$$
$$x_ <7>= 54.6380345284$$
$$x_ <8>= 1.91063323625$$
$$x_ <9>= -35.7884786068$$
$$x_ <10>= -33.3265597721$$
$$x_ <11>= -48.3548492212$$
$$x_ <12>= 79.7707757571$$
$$x_ <13>= -29.5052932996$$
$$x_ <14>= 33.3265597721$$
$$x_ <15>= 23.2221079925$$
$$x_ <16>= 58.4593010009$$
$$x_ <17>= 77.3088569224$$
$$x_ <18>= 155.168999443$$
$$x_ <19>= -23.2221079925$$
$$x_ <20>= 8.19381854343$$
$$x_ <21>= -27.043374465$$
$$x_ <22>= -64.742486308$$
$$x_ <23>= -20.7601891578$$
$$x_ <24>= 92.3371463714$$
$$x_ <25>= 86.0539610643$$
$$x_ <26>= -39.6097450793$$
$$x_ <27>= 96.1584128439$$
$$x_ <28>= -58.4593010009$$
$$x_ <29>= -86.0539610643$$
$$x_ <30>= -4.37255207093$$
$$x_ <31>= -92.3371463714$$
$$x_ <32>= -60.9212198355$$
$$x_ <33>= 14.4770038506$$
$$x_ <34>= -73.4875904499$$
$$x_ <35>= 89.8752275368$$
$$x_ <36>= 73.4875904499$$
$$x_ <37>= 48.3548492212$$
$$x_ <38>= 42.071663914$$
$$x_ <39>= -77.3088569224$$
$$x_ <40>= 20.7601891578$$
$$x_ <41>= -71.0256716152$$
$$x_ <42>= 16.9389226853$$
$$x_ <43>= -52.1761156937$$
$$x_ <44>= -89.8752275368$$
$$x_ <45>= -10.6557373781$$
$$x_ <46>= -7726.40729459$$
$$x_ <47>= -971.983089377$$
$$x_ <48>= -79.7707757571$$
$$x_ <49>= -67.2044051427$$
$$x_ <50>= 98.6203316786$$
$$x_ <51>= 27.043374465$$
$$x_ <52>= 64.742486308$$
$$x_ <53>= -54.6380345284$$
$$x_ <54>= 60.9212198355$$
$$x_ <55>= 10.6557373781$$
$$x_ <56>= -42.071663914$$
$$x_ <57>= -14.4770038506$$
$$x_ <58>= 39.6097450793$$
$$x_ <59>= 3426.24662565$$
$$x_ <60>= 83.5920422296$$
$$x_ <61>= -45.8929303865$$
$$x_ <62>= -8.19381854343$$
$$x_ <63>= 4.37255207093$$
$$x_ <64>= 29.5052932996$$
$$x_ <65>= 45.8929303865$$
$$x_ <66>= -98.6203316786$$
$$x_ <67>= -16.9389226853$$
$$x_ <68>= -1.91063323625$$
Для того, чтобы найти экстремумы, нужно решить уравнение
$$frac f
(производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
$$frac f
Первая производная
$$3 sin
Решаем это уравнение
Корни этого ур-ния
$$x_ <1>= 0$$
$$x_ <2>= pi$$
Зн. экстремумы в точках:
Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
Минимумы функции в точках:
$$x_ <2>= 0$$
Максимумы функции в точках:
$$x_ <2>= pi$$
Убывает на промежутках
Возрастает на промежутках
Найдем точки перегибов, для этого надо решить уравнение
$$frac<2>><2>> f
(вторая производная равняется нулю),
корни полученного уравнения будут точками перегибов для указанного графика функции:
$$frac<2>><2>> f
Вторая производная
$$3 cos
Решаем это уравнение
Корни этого ур-ния
$$x_ <1>= frac
$$x_ <2>= frac<3 pi><2>$$
Интервалы выпуклости и вогнутости:
Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
Вогнутая на промежутках
Выпуклая на промежутках
© Контрольная работа РУ – калькуляторы онлайн
