Метод золотого сечения минимум функции

Правила ввода функции

2. Примеры правильного написания F(x):
   1) 10•x•e 2x ≡ 10*x*exp(2*x)
   2) x•e -x +cos(3x) ≡ x*exp(-x)+cos(3*x)
   3) x 3 -x 2 +3 ≡ x^3-x^2+3

Не всегда можно определить заранее, сколько раз придется вычислять функцию. Метод золотого сечения почти столь же эффективен при n-2, что и метод Фибоначчи, однако при этом не требуется знать n – количество вычислений функции.
Сущность этого метода заключается в следующем. Интервал неопределенности делится на две неравные части так, что отношение длины большего отрезка к длине всего интервала равно отношению длины меньшего отрезка к длине большего (рис 3).

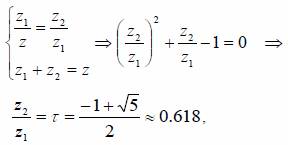
где τ – «золотое сечение»

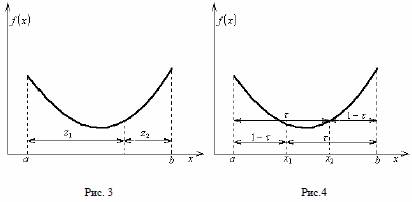
На каждом шаге этой итеративной процедуры, кроме первого, вычисляется только одно значение функции. Однако Химмельблау рекомендовал вычислять на каждом шаге две точки, для того чтобы не накапливалась погрешность, так как τ имеет приближенное значение (рис 4).
Если длина конечного интервала неопределенности равна δ, то для достижения требуемой точности число вычислений значений функции по методу золотого сечения можно найти по условию

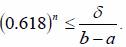
Пример . Методом золотого сечения найти точку минимума x * функции f(x) на отрезке [a;b] с точностью ε и значение целевой функции в этой точке:
f(x)=x 4 +2x 2 +4x+1=0 , [-1;0], ε=0.1
Решение. Положим a₁ = a, b₁ = b. Вычислим λ₁ = a₁ + (1- 0.618)(b₁ – a₁), μ₁ = a₁ + 0.618(b₁ – a₁).
Вычислим f(λ₁) = -0.5623, f(μ₂) = -0.2149
Итерация №1.
Поскольку f(λ₁) f(μ₂), то a₃ = -0.7639, b₃ = b₂, λ₃ = -0.618
μ₃ = a₃ + 0.618(b₃ – a₃) = -0.7639 + 0.618(-0.382 +0.7639), f(μ₃) = f(-0.5279) = -0.5623
Итерация №3.
Поскольку f(λ₃) x как середину интервала [a,b]: x=(-0.618-0.70818104)/2 = -0.66309052.
Ответ: x = -0.66309052; F(x) = -0.57965758

1. МЕТОДЫ ОДНОМЕРНОЙ ОПТИМИЗАЦИИ

При построении процесса оптимизации стараются сократить объем вычислений и время поиска. Этого достигают обычно путем сокращения количества вычислений значений целевой функции f ( x ). Одним из наиболее эффективных методов, в которых при ограниченном количестве вычислений f ( x ) достигается наилучшая точность, является метод золотого сечения.

Если известно, что функция f ( x ) унимодальная на отрезке [ a , b ], то положение точки минимума можно уточнить, вычислив f ( x ) в двух внутренних точках отрезка. При этом возможны две ситуации:

Минимум реализуется на отрезке [ a , x ₂ ] .

Минимум реализуется на отрезке [ x ₁ , b ] .

В методе золотого сечения каждая из точек x ₁ и x ₂ делит исходный интервал на две части так, что отношение целого к большей части равно отношении большей части к меньшей, т.е. равно так называемому "золотому отношению". Это соответствует следующему простому геометрическому представлению:

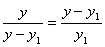
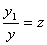
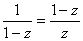
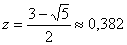
Итак, длины отрезков [ a , x ₁ ] и [ x ₂ , b ] одинаковы и составляют 0,382 от длины ( a , b ) . Значениям f ( x ₁ ) и f ( x ₂ ) определяется новей интервал ( a , x ₂ ) или ( x ₁ , b ) , в котором локализован минимум. Найденный интервал снова делится двумя точками в том же отношении, причем одна из новых точек деления сов падает с уже использованной на предыдущем шаге.

Взаимное расположение точек первых трех вычислений можно показать следующим образом:

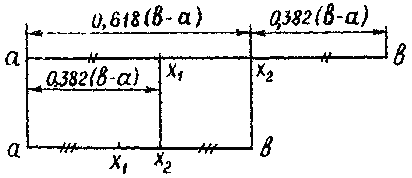
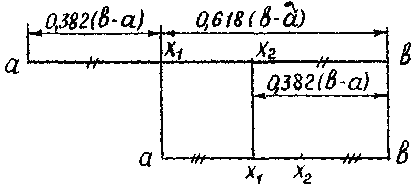
Таким образом, длина интервала неопределенности на каждом шаге сжимается с коэффициентом 0,618. На первом шаге необходимы два вычисления функции, на каждом последующем – одно.

Длина интервала неопределенности после S вычислений значений f ( x ) составляет:

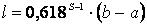
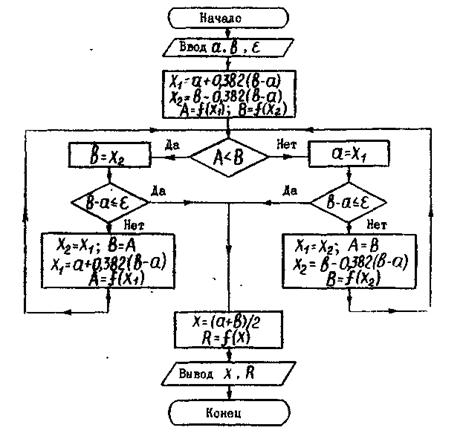
Алгоритм метода золотого сечения для минимизации функции f ( x ) складывается из следующих этапов:

1. Вычисляется значение функции f ( x₁ ) , где x₁ = a +0,382( b – a ) .
2. Вычисляется значение функции f ( x₂ ) , где x₁ = b +0,382( b – a ) .
3. Определяется новый интервал (a,x2) или (x1,b), в котором локализован минимум.
4. Внутри полученного интервала находится новая точка ( x₁ в случае 1) или ( x₂ в случае 2), отстоящая от его конца на расстоянии, составляющем 0,382 от его длины. В этой точке рассчитывается значение f ( x ). Затем вычисления повторяются, начиная с пункта 3, до тех пор, пока величина интервала неопределенности станет меньше или равна ε, где ε – заданное сколь угодно малое положительное число.

Блок-схема алгоритма поиска минимума функции f ( x ) методом золотого сечения.

Используя метод золотого сечения, минимизировать функцию f (х)= x 2 +2х на интервале (-3,5). Алина конечного интервала не­определенности не должна превосходить 0,2.

Задачи поиска максимума эквивалентны задачам поиска минимума, так как требуется лишь поменять знак перед функцией. Для поиска минимума необходимо определить интервал, на котором функция могла бы иметь минимум. Для этого можно использовать (1) графическое представление функции, (2) аналитический анализ аппроксимирующей функции и (3) сведения о математической модели исследуемого процесса (т.е. законы поведения данной функции).

Численные методы поиска минимума функции одной переменной.

Определения.
Функция f(x) имеет локальный минимум при некотором 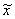, если существует некоторая конечная ξ-окрестность этого элемента, в которой 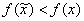, 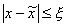. Требуется, чтобы на множестве X функция f(x) была по крайней мере кусочно-непрерывной.

Точка, в которой функция достигает наименьшего на множестве X значения, называется абсолютным минимумом функции. Для нахождения абсолютного минимума требуется найти все локальные минимумы и выбрать наименьшее значение.

Задачу называют детерминированной, если погрешностью вычисления (или экспериментального определения) функции f(x) можно пренебречь. В противном случае задачу называют стохастической. Все изложенные далее методы применимы только к детерминированным задачам.

Методы поиска минимума по нахождению корней уравнений.

Если функция f(x) аналитически дифференцируема, то решаем f / >(x) = 0 методами, изложенными в предыдущих главах. При этом условие f // (x) > 0 в найденной точке указывает нам на минимум. Для использования этих методов необходимо знать либо аналитический вид первой и второй производных, либо рассчитать их численно, если это не приведет к потере точности.

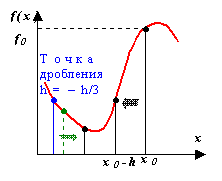
Наиболее простой метод поиска минимума. Пусть дана начальная точка x, а также величина и знак шага h, определяющие движение из этой точки в сторону предполагаемого минимума f(x). Метод заключается в последовательном дроблении исходного шага h с изменением его знака при выполнении условия f(x_k+1) > f(x_k), где k – порядковый номер вычисляемой точки. Например, как только очередное значение функции стало больше предыдущего, выполняется h = – h/3 и процесс продолжается до тех пор, пока

Данный метод является одним из самых медленных для поиска минимума. Основное достоинство данного алгоритма – возможность использования в программах управления экспериментальными исследованиями, когда значения функции f(x) последовательно измеряются с шагом h ≥ h_min.

Метод золотого сечения.

Пусть f(x) задана и кусочно-непрерывна на [x_L, x_R], и имеет на этом отрезке только один локальный минимум. Золотое сечение, о котором упоминал ещё Евклид, состоит в разбиении интервала [ _L, x_R] точкой x₁ на две части таким образом, что отношение длины всего отрезка к его большей части равно отношению большей части к меньшей:

. (2)

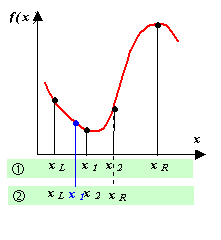
Таким образом, возьмем на отрезке две точки x₁ и x₂, симметрично относительно границ делящие исходный отрезок в отношении золотого сечения:

,

,

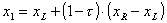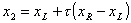где коэффициент .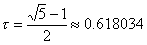

Если f(x)_{1 R} = x₂, в противном случае x_L = x₁. Оставшаяся внутри нового отрезка точка является первым приближением к минимуму и делит этот отрезок в отношении золотого сечения. Таким образом, на каждой итерации приближения к минимуму (см. рисунок) нам нужно ставить только одну точку (x₁ или x₂), в которой считать значение функции и сравнивать его с предыдущим. Условием выхода из итерационного процесса будет, подобно предыдущему случаю, условие |x₂ – x₁| ≤ ξ.

Метод отличается высокой скоростью сходимости, обычно изысканной компактностью программной реализации и всегда находит точку, минимальную на заданном интервале.

Пусть f(x) имеет первую и вторую производную. Разложим f(x) в ряд Тейлора в некоторой точке x_k, ограничиваясь при этом тремя членами разложения:

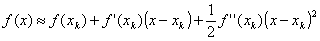. (3)

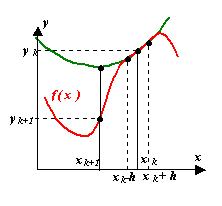
Иными словами, аппроксимируем нашу функцию в точке x_k параболой. Для этой параболы можно аналитически вычислить положение экстремума как корень уравнения первой производной от (3): 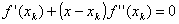. Пусть минимум аппроксимирующей параболы находится в точке x_k+1. Тогда вычислив значение функции f(x_k+1), мы получаем новую точку приближения к минимуму.

Обычно в практических реализациях данного метода не используют аналитический вид первой и второй производных f(x). Их заменяют конечно-разностными аппроксимациями. Наиболее часто берут симметричные разности с постоянным шагом h:

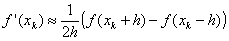
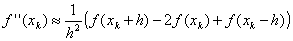
Это эквивалентно аппроксимации функции параболой, проходящей через три близкие точки x_k+h, x_k, x_k–h. Окончательное выражение, по которому можно строить итерационный процесс, таково:

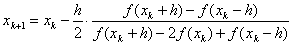. (4)

Данный метод отличается от вышеизложенных высокой скоростью сходимости. Вблизи экстремума, вплоть до расстояний

h 2 , сходимость практически не отличается от квадратичной. Однако алгоритм требует постоянного контроля сходимости. Например, итерационный процесс будет сходиться к минимуму, если

знаменатель формулы (4) должен быть >0. Если это не так, нужно сделать шаг в обратном направлении, причем достаточно большой. Обычно в итерационном процессе полагают 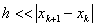. Иногда ради упрощения расчетов полагают 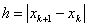, однако это существенно уменьшает скорость сходимости.

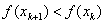• . Если это не так, то от x_k следует сделать шаг 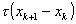с τ = ½. Если и при этом условие убывания не выполнено, уменьшают τ и вновь делают шаг.

Численные методы поиска минимума функции нескольких переменных.

Будем рассматривать методы поиска минимума 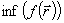в многомерных задачах на примере функции двух переменных f(x, y), так как эти методы легко аппроксимировать на случай трех и более измерений. Все эффективные методы поиска минимума сводятся к построению траекторий, вдоль которых функция убывает. Разные методы отличаются способами построения таких траекторий, так как метод, приспособленный к одному типу рельефа, может оказаться плохим для рельефа другого типа. Различают следующие типы рельефа:

1) Котловинный
(гладкая функция)



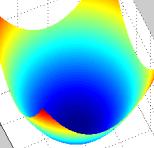
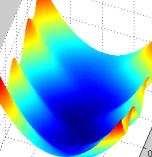
2) Истинный овраг



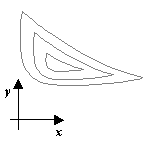
3) Разрешимый овраг





Метод координатного спуска.



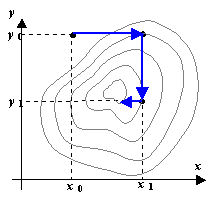
Пусть требуется найти минимум f(x, y). Выберем нулевое приближение (x , y). Рассмотрим функцию одной переменной f(x, y) и найдем ее минимум, используя любой из рассмотренных выше способов. Пусть этот минимум оказался в точке (x₁ , y). Теперь точно так же будем искать минимум функции одной переменной f(x₁ , y). Этот минимум окажется в точке (x₁ , y₁). Одна итерация спусков завершена. Будем повторять циклы, постепенно приближаясь ко дну котловины, пока не выполнится условие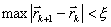

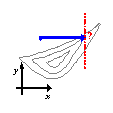Сходимость метода зависит от вида функции и выбора нулевого приближения. Вблизи невырожденного минимума гладкой функции спуск по координатам линейно сходится к минимуму. Если линии уровня образуют истинный овраг, возможен случай, когда спуск по одной координате приводит на дно оврага, а любое движение по следующей координате ведет на подъем. Процесс координатного спуска в данном случае не сходится к минимуму.
При попадании траектории спуска в разрешимый овраг сходимость становится чрезвычайно медленной. В физических задачах овражный рельеф указывает на то, что не учтена какая-то закономерность, определяющая связь между переменными. Явный учет этой закономерности облегчает использование численных методов.

Метод градиентного (наискорейшего) спуска.

Читайте также:  Iphone 5s не входит в dfu режим

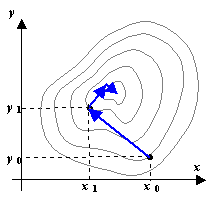В этом методе функция минимизируется по направлению, в котором она быстрее всего убывает, т.е. в направлении, обратном . Вдоль этого направления функция зависит от одной параметрической переменной t, для нахождения минимума которой можно воспользоваться любым известным методом поиска минимума функции одной переменной. Спуск из точки начального приближения 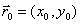против градиента до минимума t определяет новую точку 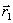, в которой вновь определяется градиент и делается следующий спуск. Условием окончания процесса, как и в случае координатного спуска, будет .

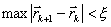С помощью метода градиентного спуска минимум гладких функций в общем случае находится быстрее, чем при использовании координатного спуска, однако нахождение градиента численными методами может свести на нет полученный выигрыш. Сходимость плохая для функций с овражным рельефом, т.е. с точки зрения сходимости градиентный спуск не лучше спуска по координатам.

Каждый спуск заканчивается в точке, где линия градиента касательна к линии (поверхности) уровня. Это означает, что каждый следующий спуск должен быть перпендикулярен предыдущему. Таким образом, вместо поиска градиента в каждой новой точке можно сосчитать градиент в начальной точке, и развернуть оси координат так, чтобы одна их осей была параллельна градиенту, а затем осуществлять спуск координатным методом.

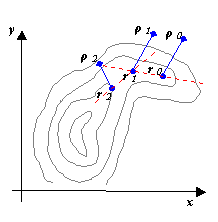Ставится задача найти минимум 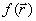для овражной функции. Для этого выбираются две близкие точк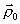и и 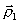, и осуществляется спуск из этих точек (любым методом), причем высокой точности сходимости не требуется. Конечные точки спуска 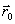и 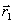будут лежать вблизи дна оврага. Затем осуществляется движение вдоль прямой, соединяюще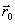й и 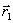в сторону уменьшения 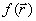(как бы вблизи дна оврага). Движение может быть осуществлено только на один шаг

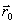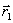h, направление выбирается из сравнения значения функции в точках и . Таким образом, находится новая точка 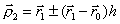. Так как возможно, что точка 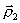уже лежит на склоне оврага, а не на дне, то из нее снова осуществляется спуск в новую точку 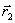. Затем намечается новый путь по дну оврага вдоль прямой, соединяющей 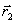и . Если 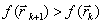– процесс прекращается, а в качестве минимума в данном овраге используется значение .

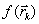Метод оврагов рассчитан на то, чтобы пройти вдоль оврага и выйти в котловину около минимума. В этой котловине значения минимума лучше уточнять другими методами.

Проблемы поиска минимума в задачах с большим числом измерений.

Пусть в n-мерном векторном пространстве задана скалярная функция 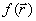. Наложим дополнительные условия 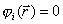, 1 ≤ i ≤ m; 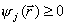, 1 ≤ j ≤ p. Условия типа равенств выделяют в пространстве некоторую (n – m)-мерную поверхность, а условия типа неравенств выделяют n-мерную область, ограниченную гиперповерхностями 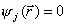. Число таких условий может быть произвольным. Следовательно, задача inf 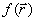есть поиск минимума функции n переменных в некоторой (n – m)-мерной области E. Функция может достигать минимального значения как внутри области, так и на ее границе. Однако перейти к (n – m)-мерной системе координат практически никогда не удается, поэтому спуск приходится вести во всем n-мерном пространстве.

Даже если нулевое приближение лежит в области E, естественная траектория спуска сразу выходит из этой области. Для принудительного возврата процесса в область E, например, используется метод штрафных функций: к 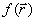прибавляются члены, равные нулю в E, и возрастающие при нарушении дополнительных условий (ограничений). Метод прост и универсален, однако считается недостаточно надежным. Более качественный результат дает использование симплекс-методов линейного программирования, однако данный вопрос в рамках настоящего курса не рассматривается.

No related posts.