- Что такое матрица поворота?
- Как матрицы вращения влияют на систему координат?
- Как сгенерировать матрицу поворота по оси X?
- Как сгенерировать матрицу поворота по оси Y?
- Как сгенерировать матрицу поворота по оси Z?
- Что такое углы Эйлера?
- Что такое рыск, качение и тангаж?
- Как мне комбинировать матрицы поворота?
- Что такое фиксация оси?
- Как правильно комбинировать матрицы вращения?
- Как сгенерировать матрицу вращения из углов Эйлера?
- Как мне перевести матрицу вращения в углы Эйлера?
- Как мне сгенерировать матрицу вращения для выбранных осей и углов?
- Как мне сгенерировать матрицу вращения, проецирующую один вектор на другой?
- Как мне использовать матрицы для перехода из одной системы координат в другую?
- Что такое матрица переноса?
- Что такое матрица скалирования?
- Что такое матрица сдвига?
- Как мне линейно интерполировать две матрицы?
- Как мне сделать кубическую интерполяцию между четырьмя матрицами?
- Как отрисовать матрицу?
- Сложение, вычитание и умножение на скаляр.
- Норма и модуль
- Обратный кватернион или сопряжение ( conjugate )
- Инверсный (inverse) кватернион
- Тождественный кватернион
- Скалярное произведение
- Вращение 3d вектора
В двумерном пространстве поворот можно описать одним углом  со следующей матрицей линейного преобразования в декартовой системе координат:
со следующей матрицей линейного преобразования в декартовой системе координат:

Поворот выполняется путём умножения матрицы поворота на вектор-столбец, описывающий вращаемую точку:
 .
.
Координаты (x’,y’) в результате поворота точки (x,y) имеют вид:
 ,
,
 .
.
Положительным углам при этом соответствует вращение вектора против часовой стрелки в обычной, правосторонней системе координат, и по часовой стрелке в левосторонней системе координат.
[править] Матрица поворота в трёхмерном пространстве
Матрицами вращения вокруг оси декартовой системы координат на угол α в трёхмерном пространстве являются:
· Вращение вокруг оси x:
 ,
,
· Вращение вокруг оси y:
 ,
,
· Вращение вокруг оси z:
 .
.
Положительным углам при этом соответствует вращение вектора против часовой стрелки в правой системе координат, и по часовой стрелке в левой системе координат, если смотреть на плоскость вращении со стороны полупространства, где значения координат оси, вокруг которой осуществляется поворот, положительные. Правая система координат связана с выбором правого базиса (см. правило буравчика).
Свойства матрицы поворота.
Свойства матрицы поворота
Если  — матрица, задающая поворот вокруг оси
— матрица, задающая поворот вокруг оси  на угол ϕ, то:
на угол ϕ, то:
· 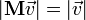

· 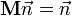
· 
·  (след матрицы вращения)
(след матрицы вращения)
· 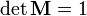 (матрица имеет единичный определитель).
(матрица имеет единичный определитель).
· если строки (или столбцы матрицы) рассматривать как координаты векторов  , то верны следующие соотношения):
, то верны следующие соотношения):
o 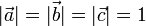
o 
o 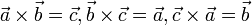
· Матрица обратного поворота получается обычным транспонированием матрицы прямого поворота, т. о. 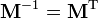 .
.
24. Алгоритм Брезенхема для растеризации отрезка.
Алгоритм Брезенхе́ма (англ. Bresenham’s line algorithm) — это алгоритм, определяющий, какие точки двумерного растра нужно закрасить, чтобы получить близкое приближение прямой линии между двумя заданными точками. Это один из старейших алгоритмов в машинной графике — он был разработан Джеком Е. Брезенхэмом (Jack E. Bresenham) в компании IBM в 1962 году. Алгоритм широко используется, в частности, для рисования линий на экране компьютера. Существует обобщение алгоритма Брезенхэма для построения кривых 2-го порядка.
Алгоритм
Отрезок проводится между двумя точками — (x,y) и (x1,y1), где в этих парах указаны колонка и строка, соответственно, номера которых растут вправо и вниз. Сначала мы будем предполагать, что наша линия идёт вниз и вправо, причём горизонтальное расстояние x1 − x превосходит вертикальное y1 − y, т.е. наклон линии от горизонтали — менее 45°. Наша цель состоит в том, чтобы для каждой колонки x между x и x1, определить, какая строка y ближе всего к линии, и нарисовать точку (x,y).
Общая формула линии между двумя точками:

Поскольку мы знаем колонку x, то строка y получается округлением к целому следующего значения:

Однако, вычислять точное значение этого выражения нет необходимости. Достаточно заметить, что y растёт от y и за каждый шаг мы добавляем к x единицу и добавляем к y значение наклона

которое можно вычислить заранее. Более того, на каждом шаге мы делаем одно из двух: либо сохраняем тот же y, либо увеличиваем его на 1.
Что из этих двух выбрать — можно решить, отслеживая значение ошибки, которое означает — вертикальное расстояние между текущим значением y и точным значением y для текущего x. Всякий раз, когда мы увеличиваем x, мы увеличиваем значение ошибки на величину наклона s, приведённую выше. Если ошибка превысила 0.5, линия стала ближе к следующему y, поэтому мы увеличиваем y на единицу, одновременно уменьшая значение ошибки на 1. В реализации алгоритма, приведённой ниже, plot(x,y) рисует точку, а abs возвращает абсолютную величину числа:
function line(x0, x1, y0, y1) int deltax := abs(x1 – x0) int deltay := abs(y1 – y0) real error := 0 real deltaerr := deltay / deltax int y := y0 for x from x0 to x1 plot(x,y) error := error + deltaerr if error >= 0.5 y := y + 1 error := error – 1.0
Проблема такого подхода — в том, что с вещественными величинами, такими как error и deltaerr, компьютеры работают относительно медленно. Кроме того, при вычислениях с плавающей точкой может накапливаться ошибка. По этим причинам, лучше работать только с целыми числами. Это можно сделать, если умножить все используемые вещественные величины на deltax. Единственная проблема — с константой 0.5 — но в данном случае достаточно умножить обе части неравенства на 2. Получаем следующий код:
Умножение на 2 для целых чисел реализуется битовым сдвигом влево.
Теперь мы можем быстро рисовать линии, направленные вправо-вниз с величиной наклона меньше 1. Осталось распространить алгоритм на рисование во всех направлениях. Это достигается за счёт зеркальных отражений, т.е. заменой знака (шаг в 1 заменяется на -1), обменом переменных x и y, обменом координат начала отрезка с координатами конца.
[править] Рисование линий
Реализация на C++:
vo > -deltaY) < error -= deltaY; x1 += signX; >if(error2 = 0) drawpixel(X1 + x, Y1 + y) drawpixel(X1 + x, Y1 – y) drawpixel(X1 – x, Y1 + y) drawpixel(X1 – x, Y1 – y) error = 2 * (delta + y) – 1 if ((delta 0) && (error > 0)) delta += 1 – 2 * –y continue x++ delta += 2 * (x – y) y–
Алгоритм сглаживания Ву.
Алгоритм Ву — это алгоритм разложения отрезка в растр со сглаживанием. Был предложен У Сяолинем (Xiaolin Wu, отсюда устоявшееся в русском языке название алгоритма) в статье, опубликованной журналом Computer Graphics в июле 1991 года. Алгоритм сочетает высококачественное устранение ступенчатости и скорость, близкую к скорости алгоритма Брезенхема без сглаживания.
Алгоритм
Горизонтальные и вертикальные линии не требуют никакого сглаживания, поэтому их рисование выполняется отдельно. Для остальных линий алгоритм Ву проходит их вдоль основной оси, подбирая координаты по неосновной оси аналогично алгоритму Брезенхема. Отличие состоит в том, что в алгоритме Ву на каждом шаге устанавливается не одна, а две точки. Например, если основной осью является Х, то рассматриваются точки с координатами (х, у) и (х, у+1). В зависимости от величины ошибки, которая показывает как далеко ушли пиксели от идеальной линии по неосновной оси, распределяется интенсивность между этими двумя точками. Чем больше удалена точка от идеальной линии, тем меньше ее интенсивность. Значения интенсивности двух пикселей всегда дают в сумме единицу, то есть это интенсивность одного пикселя, в точности попавшего на идеальную линию. Такое распределение придаст линии одинаковую интенсивность на всем ее протяжении, создавая при этом иллюзию, что точки расположены вдоль линии не по две, а по одной.


Результат работы алгоритма
Реализация в псевдокоде (только для линии по x):
function plot(x, y, c) is // рисует точку с координатами (x, y) // и яркостью c (где 0 ≤ c ≤ 1) function ipart(x) is return целая часть от x function round(x) is return ipart(x + 0.5) // округление до ближайшего целого function fpart(x) is return дробная часть x function draw_line(x1,y1,x2,y2) is if x2 BColor) and (C<>Color) then
PutPixel (x, y, Color);
PixelFill (x+1, y, BColor, Color);
PixelFill (x, y+1, BColor, Color);
PixelFill (x-1, y, BColor, Color);
PixelFill (x, y-1, BColor, Color);
Этот алгоритм не оптимизирован относительно использования стековой памяти и является одним из самых медленных алгоритмов закрашивания (в среднем только один из четырёх вызовов используется для закрашивания). Алгоритм не может заполнить области, ограниченные цветом заполнения. Можно построить подобный алгоритм и без рекурсии, если вместо стека использовать массивы.
Алгоритм закрашивания линиями.
| Данный алгоритм получил широкое распространение в компьютерной графике. От приведенного ранее он отличается тем, что на каждом шаге закрашивания рисуется горизонтальная линия, которая размещается между пикселями контура. Данный алгоритм также рекурсивный, однако количество вложенных вызовов гораздо меньше (пропорционально длине линии). Схема алгоритма такова (см.рис.): |  |
1.Имеется затравочная точка с координатами (xst, yst) и начальное направление действия рекурсивных вызовов dir=1. Параметры левой и правой границы вначале совпадают с координатой затравочной точки: xPL = xst, xPR = xst. Вызывается процедура LineFill, в которой:
2.Находятся xL и xR – левая и правая границы, между которыми проводится текущая горизонтальная линия.
3.Делается приращение у=у+dir и, между xL и xR, анализируется цвет пикселей над линией. Если он не совпадает с цветом заполнения, процедура LineFill вызывается рекурсивно с dir = 1 и xPL = xL, xLR = xR.
4.Делается приращение y=y–dir и, начиная от xL до предыдущего значения xPL анализируется цвет пикселей под линией. Если цвет пикселя отличается от цвета заполнения, процедура вызывается рекурсивно с dir = –1 и xPL = xL, xPR = xR.
5.Продолжая по той же горизонтали от предыдущего xPR до xR анализируется цвет под линией. Если цвет какого-либо пикселя отличается от цвета заполнения, процедура вызывается рекурсивно с dir = –1 и xPL = xL, xPR = xR.
Ниже приведен пример реализации этого алгоритма на языке С++:
void LineFill (int x, int y, int dir, int xPL, int xPR)
// в этой переменной будет храниться цвет пикселя
// УСТАНАВЛИВАЕМ ТЕКУЩИЕ ГРАНИЦЫ xL И xR
color = GetPixel (–xL,y);
// xL=xL-1 помещается в вызов функции
while (color != bcolor); // bcolor – цвет границы
color = GetPixel (++xR,y);
while (color !=bcolor);
Line (xL,y, xR,y, Mycolor);
//это может быть любая функция рисования линии
// АНАЛИЗИРУЕМ ПИКСЕЛИ НАД ЛИНИЕЙ
Описание алгоритма


Алгоритм разделяет плоскость на 9 частей прямыми, которые образуют стороны прямоугольника. Каждой из 9 частей присваивается четырёхбитный код. Биты (от младшего до старшего) значат «левее», «правее», «ниже», «выше». Иными словами, у тех трёх частей плоскости, которые слева от прямоугольника, младший бит равен 1, и так далее.
Алгоритм определяет код конечных точек отрезка. Если оба кода равны нулю, то отрезок полностью находится в прямоугольнике. Если битовое И кодов не равно нулю, то отрезок не пересекает прямоугольник (т.к. это значит, что обе конечные точки отрезка находятся с одной стороны прямоугольника). В прочих случаях, алгоритм выбирает конечную точку, находящуюся вне прямоугольника, находит ближайшую к ней точку пересечения отрезка с одной из линий, образующей стороны прямоугольника, и использует эту точку пересечения как новую конечную точку отрезка. Укороченный отрезок снова пропускается через алгоритм.
Реализация алгоритма для трёхмерной модели идентична двумерной реализации, за исключением того, что вместо четырёхразрядного кода применяется шестиразрядный (дополнительные два бита глубины).
28. Алгоритм разбиения средней точкой.
Последнее изменение этой страницы: 2016-04-21; Нарушение авторского права страницы
Что такое матрица поворота?
Матрица поворота используется для поворота точек вокруг
системы координат. В то время как отдельные точки привязываются к новым координатам,
расстояния между ними не меняются.
Все вращения определяются через тригонометрические функции синус и косинус.
Для двумерной системы координат, матрица вращения такая:
Если угол А равен 0, то на выходе получаем единичную матрицу:
Если угол А равен +90 градусов, то матрица такова:
Если угол А равен -90 градусов, то матрица такова:
Углы поворота, взятые с обратным знаком равны транспонированию матрицы.
Если матрица вращения умножена на транспонированную,
в результате будет единичная матрица
Как матрицы вращения влияют на систему координат?
Матрицы вращения влияют на систему координат следующим образом:
По договоренности положительные углы создают вращение по часовой стрелке,
если смотреть из центра координат в положительном направлении оси вращения.
Следуя этому правилу, в праворукой декартовой системе координат,
мы увидим следующие три вида:
Так как вращение на положительный угол создает вращение по часовой стрелке,
можно создать набор координат для каждого такого вращения.
Для упрощения рассмотрим поворот на +90:
Можно упростить так:
В матрице это будет так:
Это и есть те три базовые матрицы, которые используются в OpenGL.
Как сгенерировать матрицу поворота по оси X?
Для 4×4 матрицы:
Как сгенерировать матрицу поворота по оси Y?
Для 4×4 матрицы:
Как сгенерировать матрицу поворота по оси Z?
Для 4×4 матрицы:
Что такое углы Эйлера?
Углы Эйлера это имя, данное для набора углов поворота определённых
относительно трех осей
Их можно определить в векторном виде и хранить в структуре VECTOR.
К примеру, набор из всегда дает единичную матрицу.
Если представить углы в таком виде, то:
вращение на +90 градусов по X.
вращение на +90 градусов по Y.
вращение на +90 градусов по Z.
Что такое рыск, качение и тангаж?
Рыск, качение и тангаж это термины аэронавтики для поворота
в Эвклидовой системе координат (Углах Эйлера), относительно местной
системы координат самолета.
Представьте, что вы в самолете и смотрите вперед
Ось Z соединяет хвост и нос самолета.
X от конца левого крыла к концу правого крыла.
Y указывает с земли в небо.
Тангаж- поворот по Х, Рыск – поворот по Y, Качение – поворот по Z.
Как мне комбинировать матрицы поворота?
Матрицы поворота комбинируются при помощи матричного умножения.
Так что порядок умножения очень важен.
Что такое фиксация оси?
Фиксация – проблема, появляющаяся при использовании углов Эйлера.
Так как конечный поворот зависит от порядка умножения, может произойти так,
что одна ось вращения отобразиться на другую ось.
Из-за чего станет невозможно повернуть объект в нужной оси.
К примеру, если вращать объект в порядке Z,Y,X и повернуть
по оси Y на 90 градусов.
В этом случае, вращение по оси Z будет произведено первым,
а значит, будет проведено, верно. По оси Y также корректно.
Однако после вращения по Y, ось X будет вращаться по оси Z.
Так что любое вращение по X на самом деле будет вращать по Z.
Единственное решение этой проблемы – использовать Кватернионы.
Как правильно комбинировать матрицы вращения?
На самом деле, нет "правильного пути". Однако для возможности предсказать
результат, некоторая организация необходима. Это также нужно,
при создании полноценной 3D матричной библиотеки.
Самый простой путь повернуть объект:
где M финальная матрица вращения, и X,Y,Z матрицы вращения по осям.
Они опишет поворот по оси Х (тангаж), затем по Y(рыск)
и в конце по Z(качение).
Однако со стороны наблюдателя порядок вращений будет обратным.
К примеру, если ты стоишь и поворачиваешься налево,
то все в поле твоего зрения движется вправо.
Однако кто-либо кто смотрит на тебя, скажет, что ты повернулся направо.
Так что вид из камеры нужно моделировать в таком порядке:
Это обратная матрица вращения генерируется,
если камера считается как еще один объект.
Как сгенерировать матрицу вращения из углов Эйлера?
На первый взгляд, самый явный способ создать матрицу вращения из углов Эйлера
это создать каждую матрицу отдельно и умножить их друг на друга.
Однако этот способ очень затратный в терминах времени обработки.
Для матрицы 4х4 гарантированно 10 элементов будут равны 0, два равны 1,
и четыре оставшихся будут иметь какое-то значение,
больше 75% всех матричных операций пройдет впустую. И это не считая
настройку и инициализацию каждой матрицы.
Вместе, больше 75% всех операций будут потрачены на нулевой или единичный результат.
Нужно более эффективное решение. К счастью, есть другой путь, определения
конечной матрицы.
Если все три матрицы записать в алгебраической форме,
то мы получим следующее выражение:
Где M – конечная матрица,
X – матрица вращения по X,
Y – матрица вращения по Y,
Z – матрица вращения по Z,
Расписав мы получим:
где A,B косинус и синус вращения по оси X,
C,D косинус и синус вращения по оси Y,
E,F косинус и синус вращения по оси Z,
Законченый алгоритм будет таким:
Оптимизированный алгоритм требует всего 12 умножений, 6 вычитаний
и 18 присваиваний.
Как видно при использовании оптимизированного алгоритма, мы получили
прирост производительности в 1000%.
Как мне перевести матрицу вращения в углы Эйлера?
Эта операция обратная к прошлому вопросу.
Дана матрица вращения:
где A,B косинус и синус угла по оси X,
C,D косинус и синус угла по оси Y,
E,F косинус и синус угла по оси Z,
При использовании Сишной структуры для матрицы 4х4,
индексы элементов будут такими:
Сравнивая эти таблицы, можно увидеть, что элемент [2] отвечает значению -D
или -sin(Y). Значит, вращение по Y можно рассчитать через арксинус.
Передав полученное значение в косинус, получим значение C.
Если C не равно 0, то вращение в X и Z, можно получить из третьей колонки
и первого ряда соответственно:
Углы могут быть получены из деления каждой пары значений на С и получения
ответа через арктангенс.
Если C равно 0, то эти вычисления невозможны. В этом случае поворот
по Y будет либо -90, либо 90. Так что D будет иметь значения либо 1, либо -1.
В этом случае мы получаем фиксацию оси. Поворот по оси X и Z будет
производиться на одной оси. Это можно увидеть из расчета осей поворота.
Эти два значения отвечают за синус и косинус одной оси вращения.
Алгоритм будет таким:
Как мне сгенерировать матрицу вращения для выбранных осей и углов?
Есть лишь один способ создать этот тип матрицы поворота через математику кватернионов.
Смотри вопрос В54.
Как мне сгенерировать матрицу вращения, проецирующую один вектор на другой?
Когда создаешь анимационные программы, часто необходимо найти
матрицу поворота для проецирования направления одного вектора на другой.
Это проблему можно представить в виде двух векторов исходящих из одной точки.
То все поле значений вращения сформирует сферу.
В теории, есть бесконечное число осей вращения и углов, которыми можно
проецировать один вектор на другой. Все они лежат в плоскости
где все точки лежат на одинаковых расстояниях от обоих векторов.
Однако лишь одно решение имеет практический интерес. Это путь, который
будет иметь кротчайшее угловое расстояние между векторами.
Вращение оси по этому пути считается через векторное произведение
между двумя векторами:
Так как Земля круглая, кратчайший путь будет иметь
кратчайшее угловое вращение между двумя городами.
Как мне использовать матрицы для перехода из одной системы координат в другую?
Похоже на предыдущую проблему, необходимо привести одну координатную систему к другой.
Однако, вместо того, чтобы пытаться проецировать одну координатную ось к другой,
необходимо совместить все три оси. Координатные системы представлены в виде матриц
3х3 или 4х4.
Проблема в том, чтобы найти матрицу поворота, которая бы отобразила одну матрицу на другую.
Математически это будет так:
Значит, задача состоит в поиске матрицы Mrot. Это можно сделать
через перестановку в уравнении:
Таким образом, нужную матрицу можно вычислить, умножив
обратную матрицу в оригинальной системе на финальную матрицу вращения.
Для проверки, представим, что и оригинальная и конечная матрица – единичные матрицы.
Тогда, матрица поворота должна совпадать с финальной и обратной к ней.
Единожды посчитанная, матрица вращения может быть превращена в кватернион.
Что такое матрица переноса?
Матрица переноса используется для установки объекта в 3D пространстве без его поворота.
Перенос может быть осуществлен с помощью матричного умножения
лишь при использовании 4х4 матриц.
Если перенос описан вектором [X Y Z], то матрица 4х4 будет такой:
Что такое матрица скалирования?
Матрица скалирования используется для расширения или
сжимания размеров 3D модели.
Если вектор скалирования равен [X Y Z] то матрица будет такой:
Что такое матрица сдвига?
Матрица сдвига используется для сдвига 3D модели в стороны.
К примеру, "курсивный" текс требует, чтобы каждый символ был сдвинут вправо.
В трех измерениях возможны 6 сторон сдвига:
o сдвигает X по Y
o сдвигает X по Z
o сдвигает Y по X
o сдвигает Y по Z
o сдвигает Z по X
o сдвигает Z по Y
Все 6 направлений сдвига могут быть собраны в одной матрице:
Где Sij реализует сдвиг I по J
Так что, Sxy сдвигает X по Y
Теоретически, вращение в трех измерениях может быть комбинацией сдвига в 6 направлениях.
Как мне линейно интерполировать две матрицы?
Даны две матрицы, задача найти путь для определения средних точек
в зависимости от переменной t, которая изменяется в рамках от 0.0 до 1.0.
Это можно сделать переводом двух матриц либо в углы Эйлера, либо в сферические углы (кватернионы)
и вектор переноса. В этом случае каждая матрица превращается в пару 3D векторов.
Интерполировать между этими двумя векторами можно стандартной формулой линейной интерполяции:
Это уравнение можно применять и на вектор переноса и на вектор поворота.
Однажды определенный, конечный перенос и поворот потом может быть переведен
обратно в среднюю матрицу.
Как мне сделать кубическую интерполяцию между четырьмя матрицами?
Дано четыре матрицы вращения или переноса, задача – найти способ определения
средний точек определённых параметром t.
Это можно сделать при помощи кубической интерполяции.
Как и с линейной интерполяцией четыре матрицы переводятся в соответствующие
вектора переноса и вращения (опять же, либо углы Эйлера, либо сферические углы)
Каждый из четырех векторов переводится в один вектор G. С помощью
математики сплайнов, этот вектор преобразуется в интерполированную матрицу M
Если вектор задан так:
Это можно сделать через стандартную матрично-векторное умножение.
Интерполировать можно при помощи параметрической переменной t:
Результат может быть преобразован обратно в матрицу вращ ения или переноса.
Необходимо заметить, что пути поворота могут оказаться закрученными,
это нормально, так как алгоритм пытается найти путь минимального вращения
между четырьмя векторами.
Из двух методов, сферические углы вращения дают обычно самую
лучшую интерполяцию для вращения.
Как отрисовать матрицу?
Когда используешь графическое окно для 3D анимации, бывает нужно видеть
как матрица вращения влияет на анимацию.
Однако, просто показ матрицы вращения в виде чисел не очень понятен.
Как альтернатива, можно отрисовать численные данные в виде графиков.
Похоже на графический эквалайзер в стерео, матрица вращения можно
представить в виде графика. Каждый элемент матрицы вращения отрисовывается в
виде отдельной колонки в рамке от -1 до +1.
Матрица 3х3 будет выглядеть так:
Для удобства, отрицательные значения можно красить другим цветом,
нежели положительные.
Объект обычно определяется в удобной для его описания локальной системе координат (ЛСК), а его положение в пространстве — в глобальной системе координат (ГСК).
В трёхмерном пространстве переход из одной СК в другую описывается в общем случае системой линейных уравнений:

Уравнения могут быть записаны через матрицы геометрических преобразований в однородных координатах одним из 2-х способов:

В ортогональных СК оси X, Y и Z взаимно перпендикулярны и расположены по правилу правой руки:

На рисунке справа большой палец определяет направление оси, остальные пальцы — положительное направление вращения относительно этой оси.
Все три вектора направлений есть единичными.

Ниже приводится единичная матрица для 2-х способов записи уравнений геометрических преобразований. Такая матрица не описывает ни перемещения, ни вращения. Оси ЛСК и ГСК совпадают.

Далее рассматривается матрица для второго способа матричной записи уравнений (матрица справа). Этот способ встречается в статьях значительно чаще.
При использовании матрицы вы можете игнорировать нижнюю строку. В ней всегда хранятся одни и те же значения 0, 0, 0, 1. Она добавлена для того,чтобы мы могли перемножать матрицы (напомню, что можно перемножать только квадратные матрицы).
Остальные 12 значений определяют координатную систему. Первый столбец описывает компоненты направления оси X(1,0,0). Второй столбец задает направление оси Y(0,1,0), третий – оси Z (0,0,1). Последний столбец определяет положение начала системы координат (0,0,0).
Как будет выглядеть матрица для задания ЛСК, с началом в точке (10,5,0) и повёрнутой на 45° вокруг оси Z глобальной СК, показано на рисунке.

Рассмотрим сначала ось X. Если новая система координат повернута на 45° вокруг оси z, значит и ось x повернута относительно базовой оси X на 45° в положительном направлении отсчета углов. Таким образом, ось X направлена вдоль вектора (1, 1, 0), но поскольку вектор системы координат должен быть единичным, то результат должен выглядеть так (0.707, 0.707, 0). Соответственно, ось Y имеет отрицательную компоненту по X и положительную по Y и будет выглядеть следующим образом (-0.707, 0.707, 0). Ось Z направления не меняет (0, 0, 1). Наконец, в четвертом столбце вписываются координаты точки начала системы координат (10, 5, 0).
Частным случаем матриц геометрических преобразований есть матрицы поворота ЛСК относительно базовых осей ГСК. Вектора осей ЛСК здесь выражены через синусы и косинусы углов вращения относительно оси, перпендикулярной к плоскости вращения.

От матрицы преобразований размером 4*4 можно перейти непосредственно к матрице поворота 3*3 убрав нижний ряд и правый столбик. При этом система линейных уравнений записывается без свободных элементов (лямда, мю, ню), которые определяют перемещение вдоль осей координат.
Путем перемножения базовых матриц можно получать комбинированные вращения. Ниже рассмотрены возможности комбинировать вращениями через матрицы поворота на примерах работы с углами Эйлера.


От выбора осей и последовательности вращения зависит конечный результат. На рисунках отображена следующая последовательность вращения относительно осей ЛСК:
- оси Z (угол alpha);
- оси X (угол beta);
- оси Z (угол gamma).

Можно получить результирующую матрицу, которая определяет положение ГСК относительно ЛСК. Для этого необходимо перемножить матрицы с отрицательными углами в последовательности выполнения поворотов:


Почему знак угла поворота меняется на противоположный? Объяснение этому простое. Движение относительно. Абстрагируемся и представим, что ГСК меняет положение относительно неподвижной ЛСК. При этом направление вращения меняется на противоположное.
Перемножение матриц даст следующий результат:

Результирующую матрицу можно использовать для пересчета координат из ГСК в ЛСК:

Для пересчета координат из ЛСК в ГСК используется результирующая обратная матрица.

В обратной матрице последовательность поворота и знаки углов меняются на противоположные (в рассматриваемом примере снова на положительные) по сравнению с матрицей определения положения ГСК относительно ЛСК.


Перемножение матриц даст следующий результат:

Выше был рассмотрен случай определения углов Эйлера через вращение относительно осей ЛСК. То же взаимное положение СК можно получить, выполняя вращение относительно осей ГСК:
- оси z (угол (gamma+pi/2));
- оси y (угол угол beta);
- оси z (угол (-alpha)).

Последовательность преобразований берется не откуда-то свыше, а определяется чисто на здравом смысле, используя пространственное воображение. При выборе последовательности руководствуйтесь простым правилом — преобразования не должны искажать натуральную величину параметров (углов).
Умение правильно выбирать последовательность элементарных геометрических преобразований помогает в решении множества, задач (см. Примеры геометрических преобразований).
Определение углов Эйлера через вращение относительно осей ГСК позволяет также просто получить зависимости для пересчета координат из ЛСК в ГСК через перемножение матриц поворота.

В рамках рассматриваемой задачи вместо угла gamma в матрицe Az используем угол gamma+pi/2.
Также легко можно перейти к зависимостям для пересчета координат из ГСК в ЛСК.

Обратная матрица получается перемножением обратных матриц в обратном порядке по сравнению с прямым преобразованием. При этом каждая из обратных матриц вращения может быть получена заменой знака угла на противоположный.
Детально с теоретическими основами аффинных преобразований (включая и вращение) можно ознакомиться в статье Геометрические преобразования в графических приложениях
Примеры преобразований рассмотрены в статьях:
Выбрав подходящую ось (англ. rotation axis) и угол (англ. rotation angle) можно задать любую ориентацию объекта.

Обычно хранят ось вращения в виде единичного вектора и угол поворота вокруг этой оси в радианах или градусах.
q = [ x, y, z, w ] = [ v, w ]
В некоторых случаях удобно хранить угол вращения и ось в одном векторе. Направление вектора при этом совпадает с направлением оси вращения, а его длина равна углу поворота:
q = [ x, y, z]; w=sqrt (x*x +y*y +z*z)
В физике, таким образом хранят угловую скорость. Направление вектора совпадает с направлением оси вращения, а длина вектора равна скорости (в радианах в секунду).
Можно описать рассмотренные выше углы Эйлера через Axis Angle представление в 3 этапа:
q1 = [ 0, 0, 1, alpha]; q2 = [ 1, 0, 0, beta]; q3 = [ 0, 0, 1, gamma ]
Здесь каждое вращение выполняется относительно осей текущего положения ЛСК. Такое преобразование равнозначно рассмотренному выше преобразованию через матрицы поворота:
Возникает вопрос, а можно ли 3 этапа Axis Angle представления объединить в одно, подобно матрицам поворота? Попробуем решить геометрическую задачу по определению координат последнего вектора вращения в последовательности преобразований через Axis Angle представления:
q = [ x, y, z, gamma ]

Есть ли представление q= [x, y, z, gamma] композицией последовательности из 3-х этапов преобразований? Нет! Координаты x, y, z определяют всего лишь положение оси Z ЛСК после первого и второго этапов преобразований:

При этом ось Z, отнюдь, не есть вектор вращения для Axis Angle представления, которое могло бы заменить рассмотренные 3-х этапа преобразований.
К сожалению, никакие операции (типа объединения нескольких преобразований в одно) с Axis Angle представлениями нельзя выполнить. Не будем расстраиваться. Это можно сделать через кватернионы, которые также определяют вращение через через параметры оси и угол.
Кватернион (как это и видно по названию) представляет собой набор из четырёх параметров, которые определяют вектор и угол вращения вокруг этого вектора. По сути такое определение ничем не отличается от Axis Angle представления вращения. Отличия лишь в способе представления. Как же хранят вращение в кватернионе?
q = [ V*sin(alpha/2), cos(alpha/2) ]
В кватернионе параметры единичного вектора умножается на синус половины угла поворота. Четвертый компонент — косинус половины угла поворота.
Таблица с примерами значений кватернионов:

Представление вращения кватернионом кажется необычным по сравнению с Axis Angle представлением. Почему параметры вектора умножаются на синус половины угла вращения, четвертый параметр — косинус половины угла вращения, а не просто угол?
Откуда получено такое необычное представление кватерниона детально можно ознакомиться в статье Доступно о кватернионах и их преимуществах. Хотя программисту не обязательно знать эти детали, точно также как и знать, каким образом получены матрицы преобразования пространства. Достаточно лишь знать основные операции с кватернионами, их смысл и правила применения.
Кватернион удобно рассматривать как 4d вектор, и некоторые операции с ним выполняются как над векторами.
Сложение, вычитание и умножение на скаляр.
Смысл операции сложения можно описать как «смесь» вращений, т.е. мы получим вращение, которое находится между q и q’.
Что-то подобное сложению кватернионов выполнялось при неудачной попытке объединить 3 этапа Axis Angle представления.
Умножение на скаляр на вращении не отражается. Кватернион, умноженный на скаляр, представляет то же самое вращение, кроме случая умножения на 0. При умножении на 0 мы получим «неопределенное» вращение.
Пример сложения 2-х кватернионов:
Норма и модуль
Следует различать (а путают их часто) эти две операции:
Модуль (magnitude), или как иногда говорят «длина» кватерниона:
Через модуль кватернион можно нормализовать. Нормализация кватерниона — это приведение к длине = 1 (так же как и в векторах):
Обратный кватернион или сопряжение ( conjugate )
Обратный кватернион задает вращение, обратное данному. Чтобы получить обратный кватернион достаточно развернуть вектор оси в другую сторону и при необходимости нормализовать кватернион.
Например, если разворот вокруг оси Y на 90 градусов = (w=0,707; x = 0; y = 0,707; z=0), то обратный = (w=0,707; x = 0; y = -0,707; z=0).
Казалось бы, можно инвертировать только компоненту W, но при поворотах на 180 кватернион представляется как (w=1; x = 0; y = 0; z=0), то есть, у него длина вектора оси = 0.
Фрагмент программной реализации:
Инверсный (inverse) кватернион
Существует такой кватернион, при умножении на который произведение дает нулевое вращение и соответствующее тождественному кватерниону (identity quaternion), и определяется как:
Тождественный кватернион
Записывается как q[0, 0, 0, 1]. Он описывает нулевой поворот (по аналогии с единичной матрицей), и не изменяет другой кватернион при умножении.
Скалярное произведение
Скалярное произведение полезно тем, что дает косинус половины угла между двумя кватернионами умноженную на их длину. Соответственно скалярное произведение двух единичных кватернионов даст косинус половины угла между двумя ориентациями. Угол между кватернионами это угол поворота из q в q’ (по кратчайшей дуге).
Вращение 3d вектора
Вращение 3d вектора v кватернионом q определяется как
причем вектор конвертируется в кватернион как
и кватернион обратно в вектор как
Одна из самых полезных операций, она аналогична умножению двух матриц поворота. Итоговый кватернион представляет собой комбинацию вращений — сначала объект повернули на q, а затем на q’ (если смотреть из глобальной системы координат).
Примеры векторного и скалярного перемножения 2-х векторов

векторное произведение — вектор:
Скалярное произведение — число:
Пример умножения 2-х кватернионов:

В разделе Axis Angle представление вращения была сделана неудачная попытка объединить 3 Axis Angle представления в одно . Это можно сделать опосредовано. Сначала Axis Angle представления конвертируются в кватернионы, затем кватернионы перемножаются и результат конвертируется в Axis Angle представление.
Пример конвертирования произведения 2-х кватернионов в Axis Angle представление:
Фрагмент программы на C:
Матрица поворота выражается через компоненты кватерниона следующим способом:
 где
где

Проверим формулы конвертирования на примере конвертирования произведения 2-х кватернионов в матрицу поворотов:
Определяем элемент матрицы m[0][0] через параметры кватерниона:

Соответствующее произведению кватернионов (q1 и q2) произведение матриц поворотов было получено ранее (см. Матрицы поворота и углы Эйлера):

Как видим, результат m[0][0], полученный через конвертирование, совпал с значением в матрице поворота.
Фрагмент программного кода на С для конвертирования кватерниона в матрицу поворота:
При конвертировании используется только умножения и сложения, что является несомненным преимуществом на современных процессорах.
Часто для задания вращений используют только кватернионы единичной длины, но это не обязательно и иногда даже не эффективно. Разница между конвертированием единичного и неединичного кватернионов составляет около 6-ти умножений и 3-х сложений, зато избавит во многих случаях от необходимости нормировать (приводить длину к 1) кватернион. Если кусок кода критичен по скорости и вы пользуетесь только кватернионами единичной длины тогда можно воспользоваться фактом что норма его равна 1.

Конвертирование матрицы в кватернион выполняется не менее эффективно, чем кватерниона в матрицу, но в итоге мы получим кватернион неединичной длины. Его можно нормализовать.
Фрагмент программного кода конвертирования матрицы поворота в кватернион:
