Содержание урока
Практическое задание №7
Тема: Численные эксперименты с демоверсиями моделей
1. Математическая модель полета снаряда
1.1. Запустить программу «Демонстрационная математическая модель». Познакомиться с работой модели в режиме без учета сопротивления воздуха и с учетом сопротивления воздуха.
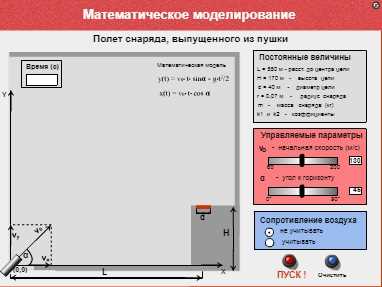 |

1.2. В режиме «Сопротивление воздуха не учитывать» провести следующий эксперимент: изменяя величину начальной скорости снаряда от 60 м/с до 200 м/с с шагом 10 м/с для каждого значения скорости подбирать величину угла выстрела, при котором произойдет попадание снаряда в цель. Желательно поиск искомого значения угла осуществлять методом деления пополам. При попадании в цель фиксировать время полета снаряда. Полученные результаты занести в таблицу.

Определить параметры выстрела, при которых цель будет поражена за наименьшее время. В тех случаях, если попасть в цель не удается, в графе времени поставить прочерк.
1.3. Повторить те же эксперименты в режиме «Сопротивление воздуха учитывать»
2. Имитационная модель системы массового обслуживания
2.1. Запустить программу «Имитационное моделирование». Познакомиться с работой программы
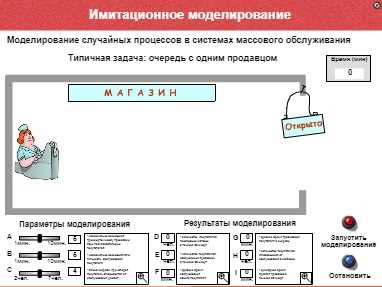 |

Пояснение. В магазине проводится эксперимент с целью совершенствования обслуживания покупателей. Эксперимент длится 60 минут. Управляемыми являются параметры А, В, С (см. описание на экране). Результатами эксперимента являются параметры D, E, F, G, H, I. Покупателей обслуживает один продавец.
2.2. Для заданных значений параметров С и А (например С=3 чел. , А=5 мин) подобрать максимально возможное В, при котором не будет покупателей, отказавшихся от совершения покупки. Для этого изменять В от 1 мин до 10 мин с шагом 1 мин. Результаты эксперимента заносить в таблицу:

2.3. Провести численный эксперимент с целью определения режима работы продавца, при котором будет обслужено наибольшее число покупателей.
- Привлечение школьников к освоению возможностей компьютерного эксперимента.
- Обобщение и применение для решения реальной задачи знаний по физике
- Развитие познавательного интереса, творческой активности учащихся, умения использовать дополнительную литературу.
- Обобщение знаний основного программного материала.
- Обучающие
– повторение и проверка умений учащимися пользоваться современными информационными технологиями.
- Развивающие –
- Воспитательные
развитие логического мышления, воображения, зрительного внимания, умения мыслить.
– развивать навыки работы в группах, информационную культуру.
Вид урока: изучение и первичное закрепление новых знаний и способов деятельности
I. Организационный момент
II. Актуализация опорных знаний
1. Модель есть замещение изучаемого объекта другим объектом, который отражает:
А) все стороны данного объекта;
Б) некоторые стороны данного объекта;
В) существенные стороны данного объекта;
Г) несущественные стороны данного объекта.
2. Информационной моделью организации занятий в школе является:
А) правила поведения учащихся;
Б) расписание уроков;
В) список класса;
Г) перечень учебников.
3. Материальной моделью является:
4. Генеалогическое дерево семьи является:
А) табличной информационной моделью;
Б) иерархической информационной моделью;
В) сетевой информационной моделью;
Г) словесной информационной моделью.
5. Знаковой моделью является:
А) анатомический муляж;
Б) макет здания;
В) модель корабля;
Г) диаграмма.
6. Устное представление информационной модели называется:
А) графической моделью;
Б) словесной моделью;
В) табличной моделью;
Г) логической моделью.
7. Упорядочение информации по определенному признаку называется:
А) сортировкой;
Б) формализацией;
В) систематизацией;
Г) моделированием.
8. Как называется упрощенное представление реального объекта:
9. Процесс построения модели называется:
А) моделирование;
Б) конструирование;
В) экспериментирование;
Г) проектирование.
10. Информационная модель, состоящая из строк и столбцов, называется:
III. Объяснение нового материала. [3]
Современным инструментом для информационного моделирования является компьютер. Конечно, на компьютере можно писать тексты (строить вербальные модели), рисовать карты и схемы (графические модели), строить таблицы (табличные модели). Но при таком использовании компьютера в моделировании его возможности проявляются не в полной мере. Главное преимущество компьютера перед человеком – способность к быстрому счету. Современные компьютеры считают со скоростями в сотни тысяч, миллионы и даже миллиарды операций в секунду.
Учитывая, что расчеты производятся над многозначными числами (10 – 20 десятичных цифр), вычислительные способности компьютера нельзя даже сравнивать с человеческими. Эти феноменальные вычислительные возможности проявляются, прежде всего, в компьютерном математическом моделировании.
Математическая модель – это описание моделируемого процесса на языке математики.
После появления компьютеров стало возможным проводить расчеты сложных математических моделей за приемлемое время. Например, рассчитать погоду на завтрашний день до его наступления. Ученые перестали себя ограничивать в сложности создаваемых математических моделей, полагаясь на быстродействие компьютеров.
Компьютерная математическая модель – это программа, реализующая расчеты состояния моделируемой системы по ее математической модели.
Использование компьютерной математической модели для исследования поведения объекта моделирования называется вычислительным экспериментом.
Рассмотрим математическая модель полета снаряда
1.1. Запускаем программу «Демонстрационная математическая модель» [4]. Познакомимся с работой модели в режиме без учета сопротивления воздуха и с учетом сопротивления воздуха.
1.2. В режиме «Сопротивление воздуха не учитывать» можно провести следующий эксперимент: изменяя величину начальной скорости снаряда от 60 м/с до 200 м/с с шагом 10 м/с для каждого значения скорости подбирать величину угла выстрела, при котором произойдет попадание снаряда в цель. При попадании в цель нужно фиксировать время полета снаряда. Полученные результаты необходимо занести в таблицу.
| V0 (м/с) | a (град) | t (c) |
Определим параметры выстрела, при которых цель будет поражена за наименьшее время. В тех случаях, если попасть в цель не удается, в графе времени нужно поставить прочерк.
1.3. Повторим те же эксперименты в режиме «Сопротивление воздуха учитывать».
IV Практическая работа учащихся
Построить математическую модель физического процесса движения тела, брошенного под углом к горизонту. Выяснить зависимость расстояния и время полета тела от угла броска и начальной скорости. Угол броска и начальная скорость являются главными факторами процесса моделирования.
При расчетах будем использовать следующие допущения:
Начало системы координат расположено в точке бросания;
Тело движется вблизи поверхности Земли, т. е. ускорение свободного падения постоянно и равно 9,81 м/с^2
Сопротивление воздуха не учитывается, поэтому движение по горизонтали равномерное.
Пусть V0 – начальная скорость (м/с), a- угол бросания (радиан), L – дальность полета (м).
Движение тела, брошенного под углом к горизонту, описывается следующими формулами:
Vx= V0*соs a – горизонтальная составляющая начальной скорости,
Vy=V0*sin a – вертикальная составляющая начальной скорости,
x =Vx*t – так как движение по горизонтали равномерное,
y =Vy*t – g*t ^2/2 – так как движение по вертикали равноускоренное с отрицательным ускорением.
Искомым в этой задаче будет значение x=L,при котором y= 0
Дано:
V0 – начальная скорость (м/с), α- угол бросания (радиан).
Найти:
L – дальность полета (м).
Связь
(1) L=Vx*t – дальность полета,
(2) 0= Vy*t – g*t ^2/2 – точка падения,
(3) Vx = cos a – горизонтальная проекция вектора начальной скорости,
(4) Vy= V0*sin a – вертикальная проекция вектора начальной скорости,
g= 9,81 — ускорение свободного падения, V0>0, 0 12.02.2012
Ответы на вопрос

ха-ха-ха)) учебник по информатике за 10
program str999; uses crt; var s: string; begin writeln(‘введіте фразу’); read(s); if (s=’край озер’) then writeln (‘край озер лесов и рек’); if (s=’я учусь в школе’) then writeln (‘я учусь в 10-м классе’) end.
потхоньку буду дополнять, не так все быстро))
program р_1; uses crt; var s: string; begin writeln(‘введите фразу’); read(s); if (s=’моя родина беларусь’) then writeln (‘беларусь моя родина’); if (s=’люблю цябе мой родны кут’) then writeln (‘мой родны кут люблю цябе’) end.

может быть крик?
решение должно иметь од 20 до 5000

первым кому удалось расшифровать египетские иероглифы, был французкий ученый жан-франсуа шампольон (1790-1832). он составил полный список иероглифов и их гречиских эквивалентов создав тем самым основу для перевода всех египетских текстов.

наименьшее 4-х разрядное число в системе счисления с основанием 5 = 1000₅.
наибольшее 4-х разрядное число в системе счисления с основанием 5 = 4444₅.
переведем эти числа в десятичную систему счисления:
4444₅ = (10000₅ – 1₅) = 5⁴ – 1 = 624
количество всех 4-х разрядных чисел в системе счисления с основанием 5 равно: 624 – 125 + 1 = 500
