При проецировании прямой на какую-либо плоскость проекций проецирующие лучи, проходящие через точки прямой, образуют проецирующую плоскость, которая пересекает плоскость проекции по прямой (рис. 4.18). Следовательно, проекцией отрезка будет отрезок прямой. Чаще всего проекция отрезка меньше самого отрезка, так как его проекция (ab) является частью катета прямоугольной: треугольника (ВbМ), а отрезок (АВ) — частью гипотенузы. Так как Mb а’ах, т. е. ZB>ZA, и точка В ближе к плоскости V, чем точка А, так как bbxx, т. е. YB Стр 4 из 8 4 5 6 7 8
Для продолжения скачивания необходимо пройти капчу:
 Проекция точки на плоскость. Проекция прямой на плоскость |
|
Угол между прямой и плоскостью |
|
Теорема о трех перпендикулярах. Обратная теорема |
Проекция прямой на плоскость
Определение 1. Ортогональной проекцией точки на плоскость называют основание перпендикуляра, опущенного из этой точки на плоскость.
Рассмотрим рисунок 1, на котором изображены прямая p, перпендикулярная к плоскости α и пересекающая плоскость α в точке O.
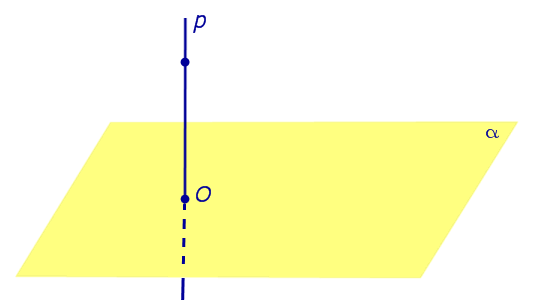
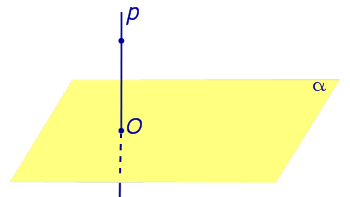
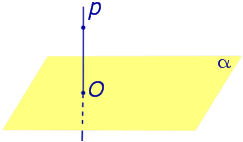
Точка O является ортогональной проекцией на плоскость α каждой точки прямой p.
Замечание 1. Рассматриваемый в данном разделе случай ортогонального проектирования точки на плоскость α представляет собой частный случай более общего понятия проектирования точки на плоскость параллельно некоторой прямой, необязательно перпендикулярной к плоскости. Такое проектирование используется в нашем справочнике при определении понятия «призма».
Замечание 2. Если это не приводит к разночтениям, для упрощения формулировок термин «ортогональная проекция на плоскость» часто сокращают до термина «проекция на плоскость».
Определение 2. Проекцией фигуры a на плоскость α называют фигуру a’, образованную проекциями всех точек фигуры a на плоскость α.
Определение 3. Прямую, пересекающую плоскость и не являющуюся перпендикуляром к плоскости, называют наклонной к этой плоскости (рис. 2).
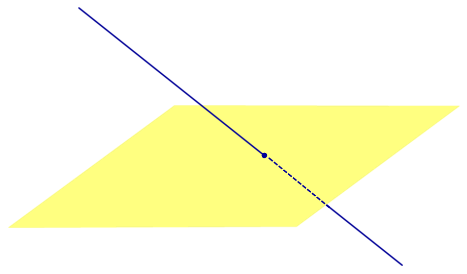
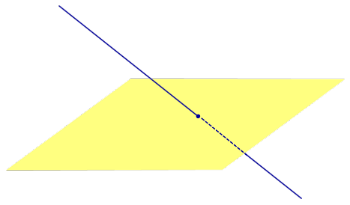
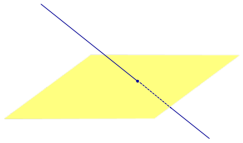
Все возможные случаи, возникающие при ортогональном проектировании прямой на плоскость представлены в следующей таблице
Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α.
На рисунке прямая PO, где P – любая точка прямой a, является перпендикуляром к плоскости α.
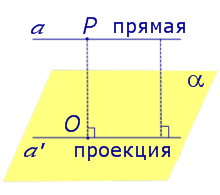
Если прямая a параллельна плоскости α , то проекцией прямой a является прямая a’, лежащая в плоскости α, параллельная прямой a и проходящая через основание O перпендикуляра PO.
Если прямая a лежит в плоскости, то ее проекция a’, совпадает с прямой a .
Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O , то точка O и является проекцией этой прямой на плоскость α.
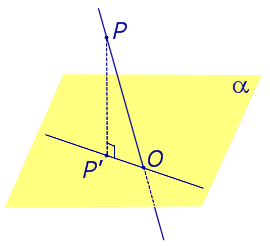
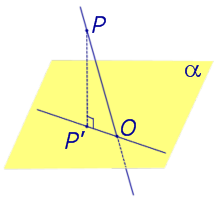
Если прямая PO пересекает плоскость α в точке O и является наклонной к плоскости α, а точка P’ является проекцией произвольной точки P этой прямой на плоскость α, то прямая P’O, лежащая в плоскости α, является проекцией прямой PO на плоскость α.
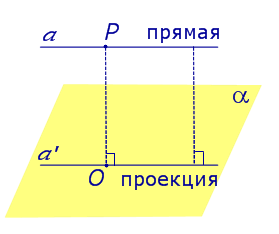
На рисунке прямая PO, где P – любая точка прямой a, является перпендикуляром к плоскости α.
Если прямая a параллельна плоскости α , то проекцией прямой a является прямая a’, лежащая в плоскости α, параллельная прямой a и проходящая через основание O перпендикуляра PO.
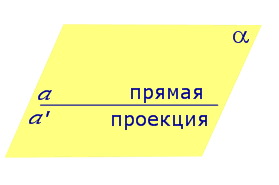
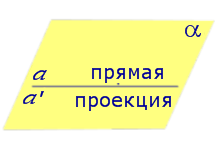
Если прямая a лежит в плоскости, то ее проекция a’, совпадает с прямой a .
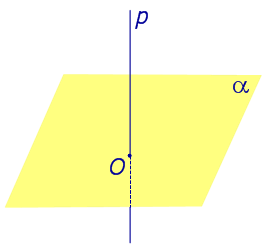
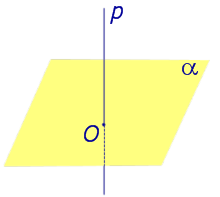
Если прямая перпендикулярна плоскости α и пересекает плоскость α в точке O , то точка O и является проекцией этой прямой на плоскость α.
Угол между прямой и плоскостью
Все возможные случаи, возникающие при определении понятия угла между прямой и плоскостью, представлены в следующей таблице.
| Фигура | Рисунок | Свойство проекции |
| Наклонная к плоскости α | |
|
| Прямая, параллельная плоскости | |
|
| Прямая, лежащая на плоскости | |
|
| Прямая, перпендикулярная к плоскости | |
Углом между наклонной к плоскости (прямая PO ) и плоскостью называют угол между этой наклонной и ее проекцией на плоскость (прямая P’O. )
На рисунке это угол φ
Если прямая параллельна плоскости, то угол между прямой и плоскостью считается равным нулю.
Если прямая лежит в плоскости, то угол между прямой и плоскостью считается равным нулю.
Если прямая перпендикулярна плоскости, то угол между прямой и плоскостью считается равным 90° ( 
радиан).
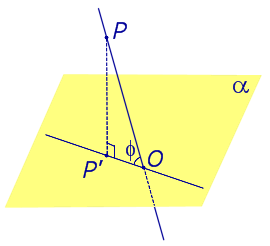
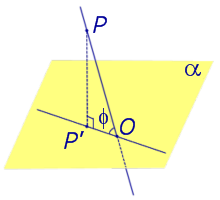
Углом между наклонной к плоскости (прямая PO ) и плоскостью называют угол между этой наклонной и ее проекцией на плоскость (прямая P’O )
На рисунке это угол φ
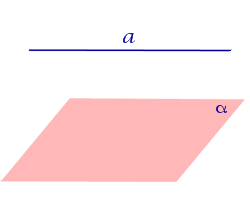
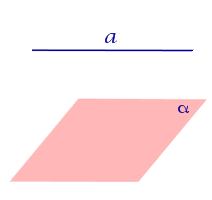
Если прямая параллельна плоскости, то угол между прямой и плоскостью считается равным нулю.
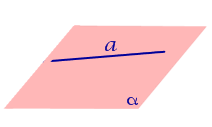
Если прямая лежит в плоскости, то угол между прямой и плоскостью считается равным нулю.
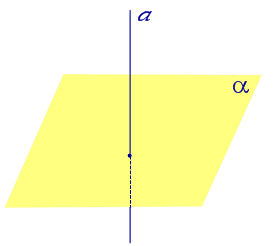
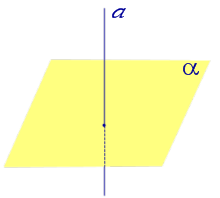
Если прямая перпендикулярна плоскости, то угол между прямой и плоскостью считается равным 90° ( радиан).
Теорема о трех перпендикулярах
Теорема о трех перпендикулярах. Если наклонная a к плоскости α перпендикулярна к прямой b, лежащей на плоскости α, то и проекция наклонной a’ на плоскость α перпендикулярна к прямой b.
Доказательство. Рассмотрим следующий рисунок 3.
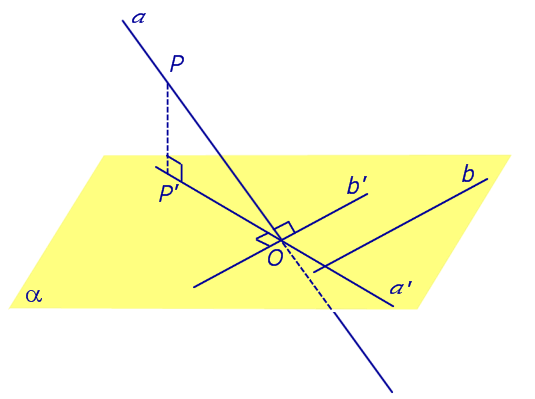
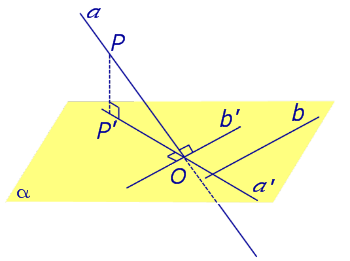
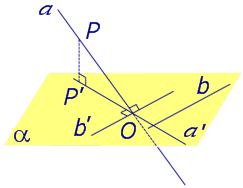
На рисунке 3 буквой O обозначена точка пересечения наклонной a с плоскостью α. Точка P – произвольная точка на прямой a, а точка P’ – это проекция точки P на плоскость α. Проведем через точку O прямую b’, параллельную прямой параллельную прямой b. Если прямая b проходит через точку O, то прямая b’, совпадет с прямой b.
Поскольку PP’ – перпендикуляр к плоскости α, то прямая PP’ перпендикулярна к прямой b’. Прямая a перпендикулярна к прямой b’ по условию. Таким образом, прямая b’ перпендикулярна к двум пересекающимся прямым PO и PP’, лежащим в плоскости POP’. В силу признака перпендикулярности прямой и плоскости получаем, что прямая b’ перпендикулярна к плоскости POP’, откуда вытекает, что прямая b’ перпендикулярна и к прямой a’, лежащей на плоскости POP’.
Теорема, обратная теореме о трех перпендикулярах. Если проекция a’ наклонной a к плоскости α перпендикулярна к прямой b, лежащей на плоскости α, то и сама наклонная a перпендикулярна к прямой b.
Доказательство. Как и для доказательства прямой теоремы о трех перпендикулярах, воспользуемся рисунком 3.
Прямая a’ перпендикулярна к прямой b по условию обратной теоремы. Прямая PP’ перпендикулярна к прямой b’, поскольку PP’ – перпендикуляр к плоскости α. Таким образом, прямая b’, перпендикулярна к двум пересекающимся прямым P’O и PP’, лежащим в плоскости POP’. В силу признака перпендикулярности прямой и плоскости прямая b’ перпендикулярна к плоскости POP’. Тогда, в частности, прямая b’ перпендикулярна к прямой a, лежащей на плоскости POP’.
Это легко) У тебя нарисована прямая, опускаешь перпендикуляр на плоскость от этой прямой, этот перпендикуляр пересекает плоскость в определённой точке. Соединяешь 2 точки лежащие на плоскости и это проекция.
Проще говоря: прямая АВ, проводишь перпендикуляр ВH, АН – проекция, угол BHA – прямой.
“>
| Фигура | Рисунок | Определение |
| Наклонная к плоскости α | |
|
| Прямая, параллельная плоскости | |
|
| Прямая, лежащая на плоскости | |
|
| Прямая, перпендикулярная к плоскости | |