
МЕТОДИЧЕСКОЕ РУКОВОДСТВО К ЛАБОРАТОРНОЙ РАБОТЕ № 1.5
ЦЕЛЬ РАБОТЫ: изучение закономерностей механических упругих столкновений шаров; проверка законов сохранения импульса и энергии в механике при столкновениях.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: Стол с наклонной плоскостью, набор шаров, уровень, измерительная линейка.
Столкновения (удары)
Под столкновением двух или большего числа тел в широком смысле подразумеваются такие их взаимодействия, при которых между телами возникают кратковременные силы столь значительные, что роль всех других постоянно действующих сил можно считать несущественной. При этом вовсе не предполагается, что тела приходят в непосредственное соприкосновение, так называемое «столкновение». Примеры соударений: удар бильярдных шаров, попадание пули в мишень, столкновение машин на дорогах, столкновение молекул и атомов, пролет космического корабля вблизи Луны и т.д. Изучение столкновений (рассеяний) микрочастиц в атомной и ядерной физике позволяет определять характер полей, создаваемых ими, и другие важные свойства. Циклотроны, синхрофазотроны и другие ускорители микрочастиц являются в сущности своей приборами для изучения столкновений.
Рассматривая столкновения, мы допускаем, что
а) исходная система отсчета инерциальная;
б) система из двух и более шаров замкнута;
в) потенциальной энергией взаимодействия шаров и их вращением пренебрегаем.
Различают упругие и неупругие столкновения. Предельными идеализированными случаями столкновений являются столкновения абсолютно упругие и абсолютно неупругие.
Если после столкновения внутреннее состояние тел изменяется, например, тела не восстанавливают свою первоначальную форму, или столкновение сопровождается превращением кинетической энергии тел в другие виды энергии, то такое столкновение называется неупругим.
Столкновение тел называется абсолютно неупругим, если по его завершению тела движутся как единое целое. В этом случае имеет место потеря механической энергии под действием диссипативных сил.
Примерами абсолютно неупругих столкновений являются попадание пули в подвижную мишень, например, в ящик с песком, подвешенный на веревке. Пуля, застряв в песке, остается в ящике и движется дальше вместе с ним. Шары из пластилина, воска или глины при столкновении обычно слипаются и затем движутся как единое целое. Аналогичное поведение наблюдается при столкновении двух разноименных ионов, сопровождающееся образованием молекулы, захвате свободного электрона положительным ионом и т.д.
Физические явления при столкновении тел довольно сложны. Сталкивающиеся тела деформируются, возникают упругие силы трения, в телах возбуждаются колебания и волны. Если удар неупругий, то в конечном итоге все эти процессы прекращаются и в дальнейшем оба тела, соединившись вместе, движутся как единое твердое тело. Его скорость, не вдаваясь в механизм сопутствующих явлений, можно найти, используя только закон сохранения импульса.
Пусть абсолютно неупругое столкновение происходит между двумя телами массой  и
и  , движущимися со скоростями
, движущимися со скоростями  и
и  соответственно. По закону сохранения импульса
соответственно. По закону сохранения импульса
 ,
,
откуда скорость тел после столкновения  определяется выражением:
определяется выражением:
 . (1.1)
. (1.1)
Как видно из формулы (1.1), движение тел после столкновения происходит по диагонали параллелограмма, построенного на векторах  и
и  :
:

Если до столкновения линии скоростей  и
и  лежали вдоль прямой, соединяющей центры масс тел, то столкновение называется центральным, в противном случае – нецентральным. В случае центрального соударения при переходе от векторной формы записи к скалярной векторы импульсов разумно проектировать на направление, совпадающее с направлением вектора скорости одного из тел, например, первого. Тогда:
лежали вдоль прямой, соединяющей центры масс тел, то столкновение называется центральным, в противном случае – нецентральным. В случае центрального соударения при переходе от векторной формы записи к скалярной векторы импульсов разумно проектировать на направление, совпадающее с направлением вектора скорости одного из тел, например, первого. Тогда:
 (1.2)
(1.2)
В этом выражении и далее по тексту в числителе верхний знак относится к случаю, когда тела до соударения двигались в одном направлении, а нижний – когда они двигались навстречу друг другу. В обоих случаях « » является скоростью движения центра инерции системы.
» является скоростью движения центра инерции системы.
Найдем, какая часть кинетической энергии  при центральном абсолютно неупругом столкновении превращается в другие виды энергии.
при центральном абсолютно неупругом столкновении превращается в другие виды энергии.
Суммарная кинетическая энергия тел до столкновения равна:



 (1.3)
(1.3)
где  ‑ приведенная масса.
‑ приведенная масса.
Таким образом, при столкновении двух абсолютно неупругих тел происходит потеря кинетической энергии макроскопического движения, равная половине приведенной массы, умноженной на квадрат относительной скорости.
Рассмотрим один частный случай, когда 
 и
и  (с точки зрения классической электронной теории металлов это имеет место при столкновении электронов проводимости в металле с узлами кристаллической решетки).
(с точки зрения классической электронной теории металлов это имеет место при столкновении электронов проводимости в металле с узлами кристаллической решетки).
Разделим числитель и знаменатель в выражении (1.3) на  . Получаем
. Получаем
 .
.
В данном выражении, исходя из условия, что 
 и
и  , слагаемыми, содержащими
, слагаемыми, содержащими  , и дробью
, и дробью  , в силу их малости, можно пренебречь и тогда
, в силу их малости, можно пренебречь и тогда
 . (1.4)
. (1.4)
Это показывает, что при абсолютно неупругом столкновении быстрых частиц малой массы с медленной (или покоящейся) частицей большой массы, практически вся кинетическая энергия быстрой частицы преобразуется в другие виды энергии.
Таким образом, во время абсолютно неупругого столкновения в системе действуют диссипативные силы, уменьшающие кинетическую энергию макроскопического движения. Поэтому применять закон сохранения энергии в его механической форме к таким процессам, происходящим во время удара, нельзя. Но после того, как удар закончился, и сталкивающиеся тела соединились в одно тело, законом сохранения энергии уже можно пользоваться (если, конечно, в дальнейшем не действуют диссипативные силы).

| Главная | Цены | Оплата | Примеры решений | Отзывы | Ccылки | Теория | Книги | Сотрудничество | Форум |
| Теория / Физические основы механики / Лабораторная работа № 1. Изучение центрального столкновения шаров |
|
Цель работы: изучение законов упругого и неупругого столкновения. I. Теоретические сведения. Столкновение (соударение) – это кратковременное взаимодействие, при котором тела непосредственно касаются друг друга. В данной работе изучается центральное соударение шаров. Соударение называется центральным , если векторы скорости шаров до удара направлены по прямой, проходящей через их центры. Абсолютно упругим называется такое столкновение, при котором механическая энергия сталкивающихся тел сохраняется. При абсолютно упругом центральном соударении шаров кинетическая энергия сталкивающихся шаров до удара должна равняться их кинетической энергии после удара. При абсолютно неупругом соударении кинетическая энергия полностью или частично превращается во внутреннюю энергию. После удара тела либо движутся с одинаковой скоростью, либо покоятся. Закон сохранения механической энергии не выполняется. Абсолютно упругие и неупругие столкновения – это идеальные случаи. На практике они могут быть реализованы лишь с определенной степенью приближения. В произвольном случае соударения шаров справедливы законы сохранения импульса и энергии: |
.gif) |
(1) |
.gif) |
(2), где |
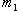 ,
, 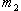 – массы шаров,
– массы шаров,
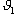 ,
, 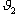 – скорости шаров до соударения,
– скорости шаров до соударения,
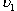 ,
, 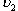 – скорости шаров после соударения,
– скорости шаров после соударения,
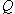 – энергия, передающаяся во внутреннюю энергию шаров.
– энергия, передающаяся во внутреннюю энергию шаров.
В случае абсолютно упругого соударения 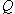 = 0, а для абсолютно неупругого соударения
= 0, а для абсолютно неупругого соударения 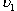 =
=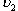
Введем критерий упругости соударения шаров. Энергетический коэффициент восстановления равен отношению полной кинетической энергии системы после удара к полной кинетической энергии до удара:
.gif) |
(3) |
Для абсолютно упругого столкновения 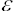 = 1.
= 1.
В нашей установке один из шаров до соударения будет покоится ( 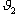 = 0). В этом случае энергетический коэффициент восстановления для абсолютно неупругого столкновения (
= 0). В этом случае энергетический коэффициент восстановления для абсолютно неупругого столкновения ( 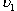 =
= 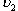 ) будет равным
) будет равным
.gif) |
(4) |
Формула (4) выводится с использованием (1) и (2).
Для произвольных столкновений шаров справедливо неравенство:
.gif) |
(5) |
II. Практическая часть
В работе ставятся две задачи:
1. Определение энергетического коэффициента восстановления для различных пар сталкивающихся шаров.
2. Проверка закона сохранения импульса при соударении.
.gif) |
На устойчивой подставке укреплена вертикальная труба (1) с подвесами для шаров (2) (рис. 1). Один из шаров (с массой 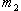 ) покоится (
) покоится (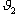 = 0), а другой (с массой
= 0), а другой (с массой 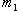 ) – отклоняется на некоторый угол. По шкале (3) отсчитываются углы отклонения шаров в градусах.
) – отклоняется на некоторый угол. По шкале (3) отсчитываются углы отклонения шаров в градусах.
.gif) |
Выразим энергетический коэффициент восстановления через углы отклонения шаров до и после удара.
Пусть шар массой отводят на высоту над начальным уровнем отсчета потенциальной энергии (0), затем отпускают. Непосредственно перед ударом шар обладает скоростью.
По закону сохранения механической энергии
.gif) |
(6), где |
.gif) |
(см. рис. 2), или |
.gif)
После соударения шары расходятся, поднимаясь на высоту 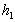 и
и 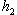 . Кинетические энергии шаров сразу после соударения будут равны потенциальным энергиям в точках, соответствующих углам отклонения
. Кинетические энергии шаров сразу после соударения будут равны потенциальным энергиям в точках, соответствующих углам отклонения 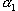 и
и 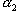 .
.
.gif) |
(7) |
.gif) |
(8), где |
.gif) ,
, .gif) .
.
Подставив (6) – (8) в (3), получим
.gif)
Зная выражения для 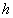 ,
, 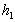 и
и 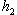 через углы
через углы 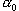 ,
, 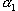 и
и 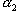 , выведем рабочую формулу для
, выведем рабочую формулу для 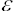 :
:
.gif) |
(9), где |
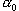 – угол отклонения шара
– угол отклонения шара 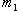 до столкновения;
до столкновения;
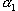 и
и 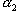 – углы отклонения шаров
– углы отклонения шаров 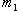 и
и 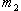 после столкновения.
после столкновения.
Учитывая, что 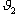 =0, запишем закон сохранения импульса для произвольного соударения:
=0, запишем закон сохранения импульса для произвольного соударения:
.gif) |
(10) |
Из формул (6) – (8) следует, что
.gif) |
; | .gif) |
; | .gif) |
. |
Зависимость 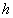 ,
, 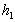 и
и 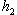 от углов
от углов 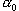 ,
, 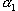 и
и 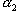 известна, поэтому
известна, поэтому
.gif) |
(11) |
Знак плюс в правой части (11) соответствует случаю, когда шар 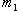 движется после соударения в первоначальном направлении, а знак минус – в противоположном.
движется после соударения в первоначальном направлении, а знак минус – в противоположном.
Порядок выполнения работы. Проведите опыт по столкновению различных пар шаров. В каждом опыте замерьте углы отклонения 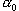 ,
, 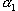 ,
, 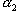 . Массы сталкивающихся шаров
. Массы сталкивающихся шаров 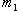 и
и 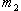 а также отношение масс заполняются автоматически. Вычислите энергетический коэффициент востановления
а также отношение масс заполняются автоматически. Вычислите энергетический коэффициент востановления 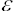 по формуле (6). Установите тип соударения, сравните экспериментальные значения
по формуле (6). Установите тип соударения, сравните экспериментальные значения 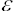 с теоретическим значением для абсолютно упругого (
с теоретическим значением для абсолютно упругого (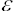 =1) и абсолютно неупругого (4) соударения. Данные занесите в протокол испытаний.
=1) и абсолютно неупругого (4) соударения. Данные занесите в протокол испытаний.
Часто задаваемые вопросы.
1. Как произвести опыт? Сначала надо выбрать шары, которые будут сталкиваться. Далее необходимо отклонить правый шар на некоторый угол (этот угол надо запомнить) и отпустить шар. После того как шары остановятся, надо занести экспериментальные данные в протокол испытаний и вычислить искомые величины.
2. Как выбрать шар? Для смены шара надо навести указатель мыши на шар, находящийся в коробке и нажать левую кнопку мыши. Шар с левой стороны выбирается из левой коробки, с правой – из правой.
3. Как отклонить шар на некоторый угол? Для того чтобы отклонить шар, прикрепленый к подвесу, необходимо навести на него указатель мыши, нажать левую кнопку мыши, и, удерживая ее, отклонить шар на некоторый угол. Угол удобнее замечать по нижней шкале.
Изучение законов упругого и неупругого столкновения шаров.
ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ
Установка для изучения соударения шаров.
Выпрямитель или трансформатор для питания электромагнита.
Рассмотрим столкновение двух шаров. Скорости, импульс и энергия шаров до и после соударения связаны законами сохранения импульса и энергии:
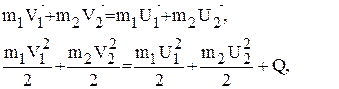 |
где В случае абсолютно упругого соударения шаров выполняется закон сохранения механической энергии и
Введем критерий упругости соударения
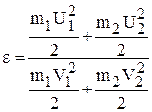 . . |
(1) |
Для абсолютно упругого соударения В случае, когда второй шар до соударения покоился и
 ,
,
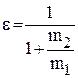 . . |
(2) |
Для частично упругих соударений будет выполняться неравенство
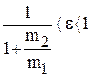 . . |
В лабораторной работе экспериментально решаются две задачи:
1) определение доли сохраненной механической энергии различных пар сталкивающихся шаров 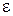 ;
;
2) экспериментальная проверка закона сохранения импульса при соударении шаров.
Пусть шары массами Выразим коэффициент
В момент удара шар
 обладает скоростью
обладает скоростью
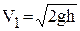 .
.
Скорости шаров сразу после соударения можно выразить через высоты
Из
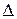 ABC (рис. 1.1) следует, что
ABC (рис. 1.1) следует, что
 ,
,
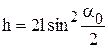 .
.
Выражение (1) для коэффициента
 , , |
(3) |
где Подстановка углов отклонения шаров
|
|
(4) |
Знак « Для малых углов
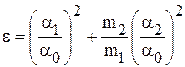 , , |
(5) |
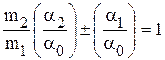 . . |
(6) |
 ОПИСАНИЕ УСТАНОВКИ
ОПИСАНИЕ УСТАНОВКИ
Конструктивно установка представляет собой треногу 1 на трех подъемных винтах, на которой укреплена труба 2, несущая подвески шаров (рис. 2). Один из шаров с массой

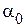 , град.
, град.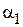 , град.
, град.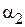 град.
град.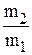 ,
,