Его можно найти несколькими способами. Рассмотрим наиболее распространенные.
а) Метод северо-западного угла.
Он заключается в том, что в начале максимально допустимое количество груза помещается в верхнюю левую (северо-западную) клетку таблицы, затем заполняется соседняя клетка в строке или в столбце, в зависимости от того, где имеются еще неиспользованные возможности перевозок.
Таким же образом (вправо и вниз) производится распределение всего количества груза.
При таком заполнении стоимость перевозки единицы груза не учитывается.
Построить опорный план транспортной задачи для исходных данных, приведенных в таблице.
| Пункты отправления | Пункты назначения | Запасы | ||
| В1 | В2 | В3 | В4 | В5 |
| А1 | ||||
| А2 | ||||
| А3 | ||||
| Потребности |
Определим тип задачи
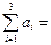
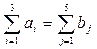следовательно, задача закрытого типа. Построим опорный план методом северо-западного угла .
| Пункты отправления | Пункты назначения | Запасы | ||
| В1 | В2 | В3 | В4 | В5 |
| А1 | ||||
| А2 | ||||
| А3 | ||||
| Потребности |
Таким образом , опорный план имеет вид:
Определим стоимость перевозок:
С=2×60+3×70+4×10+1×110+7×60+2×100=1380
б) Метод минимального элемента.
В этом случае на каждом шаге вычислений выбирают клетку с минимальным тарифом перевозок (если таких клеток несколько , то выбирают любую из них) и помещают в эту клетку максимально допустимое количество груза, с учетом имеющихся запасов и требуемых потребностей. Заполняя по этому принципу требуемое количество клеток, получим опорный план; при этом стоимость перевозок, как правило, меньше, чем в предыдущем методе.
Построить опорный план транспортной задачи для условий предыдущего примера методом минимального элемента.
| Пункты отправления | Пункты назначения | Запасы | ||
| В1 | В2 | В3 | В4 | В5 |
| А1 | ||||
| А2 | ||||
| А3 | ||||
| Потребности |
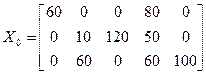
С=2×60+2×80+4×10+120+4×50+7×60+2×100=1260
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Студент – человек, постоянно откладывающий неизбежность. 10585 – 
| 7334 – 
или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Метод минимального элемента позволяет построить начальный опорный план транспортной задачи и является вариантом метода северозападного угла, учитывающим специфику матрицы С=(cij)m,n. В отличие от метода северо-западного угла данный метод позволяет сразу получить достаточно экономичный план и сокращает общее количество итераций по его оптимизации.
Схема метода: элементы матрицы С нумеруют начиная от минимального в порядке возрастания, а затем в этом же порядке заполняют матрицу Х 0 .
Пусть элементом с минимальным порядковым номером оказался элемент x 0 ij .
Тогда полагают x 0 ij = min (ai, bj)
Возможны три случая:
а) если min (ai, bj) = ai, то оставшуюся часть i-й строки заполняют нулями;
б) если min (a1, b1) = bj, то оставшуюся часть j-ro столбца заполняют нулями.
в) если ai = bj, то оставшуюся часть строки и столбца заполняют нулями.
Далее этот процесс повторяют с незаполненной частью матрицы.
Пусть элементом с k -м порядковым номером оказался х k lm. Тогда х k lm = min(a k l, b k m),
где
а k l = al – Σx g lj, g = 1..l-1
b k m = bm – Σx u im, u = 1..k-1
Возможны три случая:
а) а k l k m, тогда х k lm = а k l и оставшуюся часть строки l заполняют нулями;
б) а k l > b k m, тогда х k lm = b k m и остаток столбца m заполняют нулями;
в) а k = b k m, тогда оставшуюся часть строки l и столбца m заполняют нулями.
Как и при решении ЗЛП по планированию симплексным методом, определение оптимального плана транспортной задачи начинают с нахождения какого-нибудь ее опорного плана. Рассмотрим несколько методов нахождения такого плана.
Метод северо-западного угла. На примере конкретной задачи продемонстрируем этот метод нахождения опорного плана.
З а д а ч а 12. На три базы А1, А2, А3 поступил однородный груз в количествах, соответственно равных 140, 180, 160 ед. Этот груз требуется перевезти в пять пунктов назначения В1, В2, В3, В4, В5 соответственно в количествах 60, 70, 120, 130, 100 ед. Тарифы перевозок единичного количества груза с каждого из складов в соответствующие пункты назначения указаны в табл.16. Найти план перевозок данной транспортной задачи методом северо-западного угла.
Структурная запись задачи
Р е ш е н и е. Введем понятие маршрута – наименование клетки АiBj, где i – порядковый номер поставщика, j – порядковый номер потребителя.
Задача является закрытой, так как количество имеющегося у поставщиков грузов равно объему грузов, запрашиваемых потребителями. Здесь число пунктов отправления m=3, а число пунктов назначения n=5. Следовательно, невырожденный опорный план задачи будет определяться числом заполненных маршрутов (ненулевых переменных) в количестве 5+3-1=7.
По рассматриваемому методу заполнение маршрутов начнем с клетки, стоящей в левом верхнем углу. Потребность в грузе пункта В1 составляет 60 ед и от поставщика А1 можно эту потребность полностью удовлетворить. Иначе, по маршруту А1В1 будет запланирована поставка в размере 60 ед. Следующий потребитель В2 нуждается в поставке 70 ед груза, что также можно выполнить, доставив требуемый объем груза от поставщика А1 , у которого после первой поставки осталось 140-60=80 ед. Таким образом, по маршруту А1В2 можно запланировать доставку груза в полном объеме. Оставшийся у поставщика А1 объем груза в 10 ед запланируем доставить потребителю В3,
т.е. по маршруту А1В3. Так как ресурсы поставщика А1 полностью израсходованы, потребителю В2 оставшиеся 110 ед груза запланируем доставить по маршруту А2В3 , т.е. от поставщика А2. Пользуясь подобным алгоритмом, по маршруту А2В4 запланируем доставку 70 ед, по маршруту А3В4 доставку 60 ед и по маршруту А3В5 оставшиеся 100 ед груза (табл.17).
Результирующая таблица опорного плана задачи 12