Функция обратной матрицы в excel
Содержание

Приложение Excel выполняет целый ряд вычислений, связанных с матричными данными. Программа обрабатывает их, как диапазон ячеек, применяя к ним формулы массива. Одно из таких действий – это нахождение обратной матрицы. Давайте выясним, что представляет собой алгоритм данной процедуры.
Выполнение расчетов
Вычисление обратной матрицы в Excel возможно только в том случае, если первичная матрица является квадратной, то есть количество строк и столбцов в ней совпадает. Кроме того, её определитель не должен быть равен нулю. Для вычисления применяется функция массива МОБР. Давайте на простейшем примере рассмотрим подобное вычисление.
Расчет определителя
Прежде всего, вычислим определитель, чтобы понять, имеет первичный диапазон обратную матрицу или нет. Это значение рассчитывается при помощи функции МОПРЕД.
- Выделяем любую пустую ячейку на листе, куда будут выводиться результаты вычислений. Жмем на кнопку «Вставить функцию», размещенную около строки формул.

Запускается Мастер функций. В перечне записей, который он представляет, ищем «МОПРЕД», выделяем этот элемент и жмем на кнопку «OK».
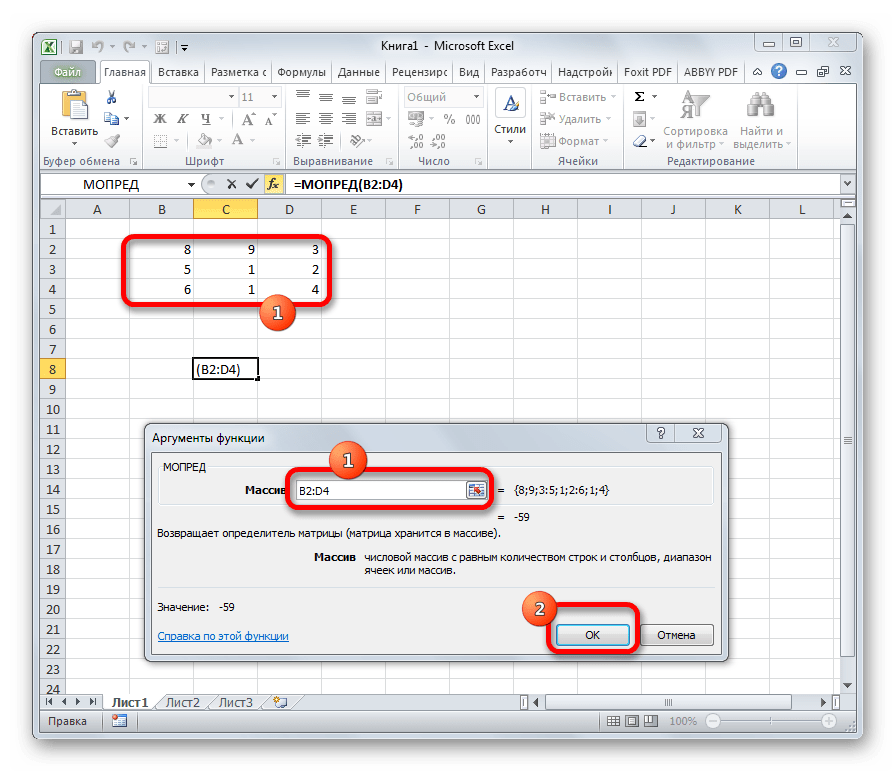
Открывается окно аргументов. Ставим курсор в поле «Массив». Выделяем весь диапазон ячеек, в котором расположена матрица. После того, как его адрес появился в поле, жмем на кнопку «OK».

Расчет обратной матрицы
Теперь можно преступить к непосредственному расчету обратной матрицы.
-
Выделяем ячейку, которая должна стать верхней левой ячейкой обратной матрицы. Переходим в Мастер функций, кликнув по значку слева от строки формул.
В открывшемся списке выбираем функцию МОБР. Жмем на кнопку «OK».

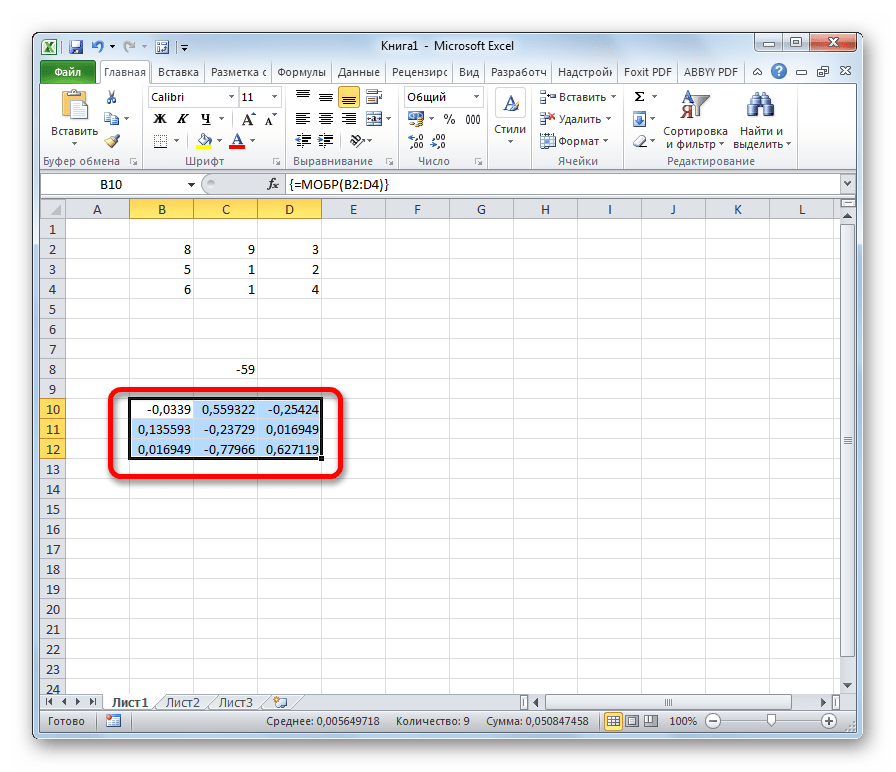
Как видим, появилось значение только в одной ячейке, в которой была формула. Но нам нужна полноценная обратная функция, поэтому следует скопировать формулу в другие ячейки. Выделяем диапазон, равнозначный по горизонтали и вертикали исходному массиву данных. Жмем на функциональную клавишу F2, а затем набираем комбинацию Ctrl+Shift+Enter. Именно последняя комбинация предназначена для обработки массивов.
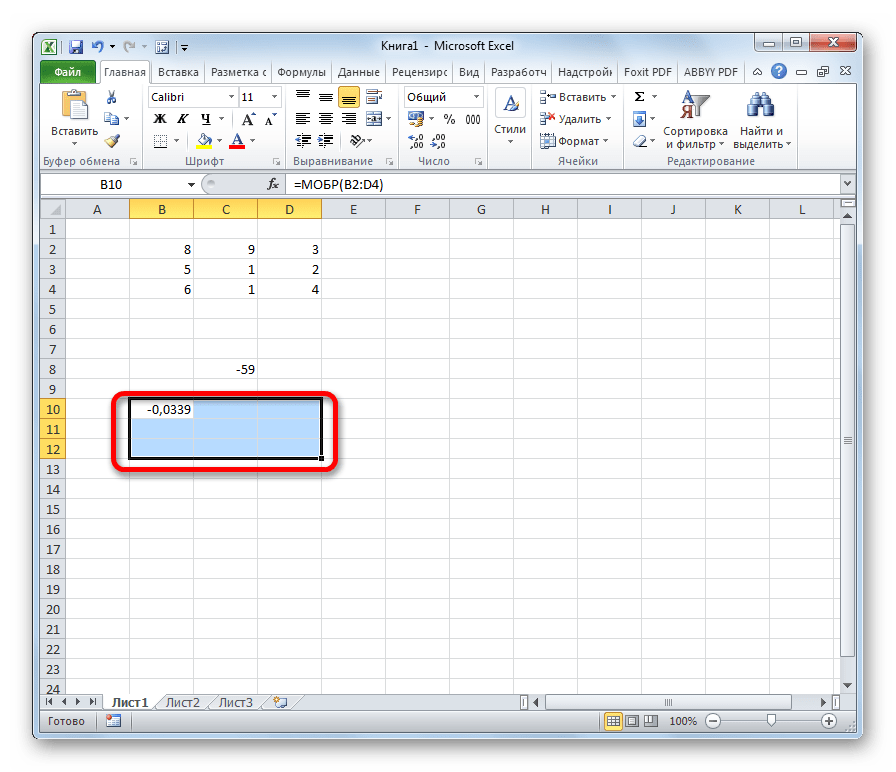
- Как видим, после этих действий обратная матрица вычислена в выделенных ячейках.
- Массив(обязательный аргумент) — числовой массив, содержащий матрицу с одинаковым числом столбцов и строк.
- В том случае, когда исходная матрица является вырожденной (определитель равен нулю), то функция вернет ошибку #ЧИСЛО!;
- Если число строк и столбцов в матрице не совпадает, то функция возвратит ошибку #ЗНАЧ!;
- Функция также вернет ошибку #ЗНАЧ!, если хотя бы один из элементов матрицы является пустым или записан в текстовом виде.
- выделить диапазон 2 х 2, который не пересекается с исходным диапазономА8:В9, например, Е8:F9
- в Cтроке формул ввести формулу = МОБР (A8:B9) и нажать комбинацию клавиш CTRL+SHIFT+ENTER, т.е. нужно ввести ее как формулу массива (формулу можно ввести прямо в ячейку, предварительно нажав клавишу F2)
- Вычисляем определитель матрицы А (далее – Det(A)) и убеждаемся, что он отличен от нуля (в противном случае матрица А необратима)
- Строим матрицу из алгебраических дополнений элементов исходной матрицы
- Транспонируем матрицу из алгебраических дополнений
- Умножаем каждый элемент транспонированной матрицы из алгебраических дополнений на 1/Det(A) и получаем обратную матрицу
На этом расчет можно считать завершенным.
Если вы производите расчет определителя и обратной матрицы только при помощи ручки и бумаги, то над этим вычислением, в случае работы над сложным примером, можно ломать голову очень долго. Но, как видим, в программе Эксель данные вычисления производятся очень быстро, независимо от сложности поставленной задачи. Для человека, который знаком с алгоритмом подобных расчетов в этом приложении, все вычисление сводится к чисто механическим действиям.
Отблагодарите автора, поделитесь статьей в социальных сетях.
Подробно рассмотрим особенности вычисления обратной матрицы в Excel и примеры использования функции МОБР.
В первую очередь освежим в памяти, что обратная матрица — это матрица (записывается как A -1 ), при умножении которой на исходную матрицу (A) дает единичную матрицу (E), другими словами выполняется формула:
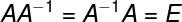
Из определения следует важное свойство, что обратная матрица определена только для квадратных (т.е. число строк и столбцов совпадает) и невырожденных матриц (т.е. определитель отличен от нуля).
Как найти обратную матрицу в Excel?
В отличие от транспонированной матрицы, вычислить обратную матрицу технически несколько сложнее.
Посчитать обратную матрицу можно через построение матриц алгебраических дополнений и определителя исходной матрицы.
Однако сложность вычисления по данному алгоритму имеет квадратичную зависимость от порядка матрицы.
К примеру, для обращения квадратной матрицы 3-го порядка нам необходимо будет дополнительно сделать 9 матриц алгебраических дополнений, транспонировать итоговую созданную матрицу и поэлементно разделить на определитель начальной матрицы, что затрудняет возможность подобного расчета в Excel.
Поэтому воспользуемся стандартной функцией МОБР, которая позволит найти обратную матрицу:
Функция МОБР
Синтаксис и описание функции МОБР в Excel:
МОБР(массив)
Возвращает обратную матрицу (матрица хранится в массиве).
Рассмотрим расчет обратной матрицы посредством функции МОБР на конкретном примере.
Предположим у нас имеется следующая квадратная матрица 3-го порядка:
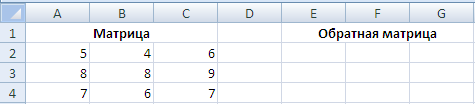
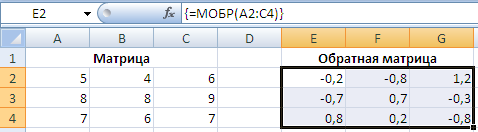
Выделяем диапазон пустых ячеек E2:G4, куда мы в дальнейшем поместим обратную матрицу.
Не снимая выделения ячеек вводим формулу =МОБР(A2:C4) и нажимаем комбинацию клавиш Ctrl + Shift + Ввод для расчета формулы массива по данному диапазону:
При работе с функцией МОБР могут возникнуть следующие ошибки:
Для вычисления обратной матрицы в MS EXCEL существует специальная функция МОБР() или англ. MINVERSE .
Понятие обратной матрицы определено только для квадратных матриц, определитель которых отличен от нуля.
СОВЕТ: О нахождении определителя матрицы читайте статью Вычисление определителя матрицы в MS EXCEL
Матрица А -1 называется обратной для исходной матрицы А порядка n, если справедливы равенства А -1 *А=Е и А*А -1 =Е, где Е единичная матрица порядка n.
Для вычисления обратной матрицы в MS EXCEL существует специальная функция МОБР() .
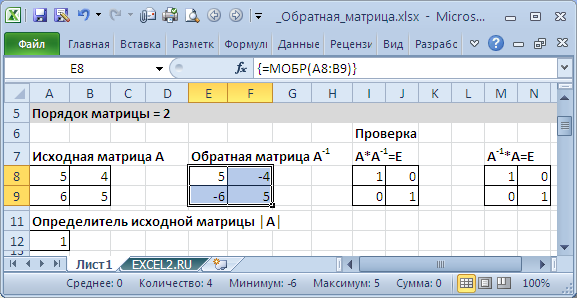
Если элементы исходной матрицы 2 х 2 расположены в диапазоне А8:В9, то для получения транспонированной матрицы нужно (см. файл примера ):
Если матрица большей размерности, то перед вводом формулы нужно выделить соответственно больший диапазон ячеек.
Массив может быть задан не только как интервал ячеек, например A8:B9, но и как массив констант, например =МОБР(<5;4: 3;2>) . Запись с использованием массива констант позволяет не указывать элементы в отдельных ячейках, а разместить их в ячейке вместе с функцией. Массив в этом случае указывается по строкам: например, сначала первая строка 5;4, затем через двоеточие записывается следующая строка 3;2. Элементы отделяются точкой с запятой.
Ссылка на массив также может быть указана как ссылка на именованный диапазон.
Некоторые квадратные матрицы не могут быть обращены: в таких случаях функция МОБР() возвращает значение ошибки #ЧИСЛО!. Матрицы не могут быть обращены, у которых определитель равен 0.
Если функция МОБР() вернула значение ошибки #ЗНАЧ!, то либо число строк в массиве не равно числу столбцов, либо какая-либо из ячеек в массиве пуста или содержит текст. Т.е. функция МОБР() пустую ячейку воспринимает не как содержащую 0 (как например, это делает СУММ() ), а как ошибочное значение.
Вычисление обратной матрицы с помощью матрицы из алгебраических дополнений
СОВЕТ: Этот раздел стоит читать только продвинутым пользователям MS EXCEL. Кроме того материал представляет только академический интерес, т.к. есть функция МОБР() .
В файле примера приведен расчет обратной матрицы 3-го порядка через матрицу алгебраических дополнений.
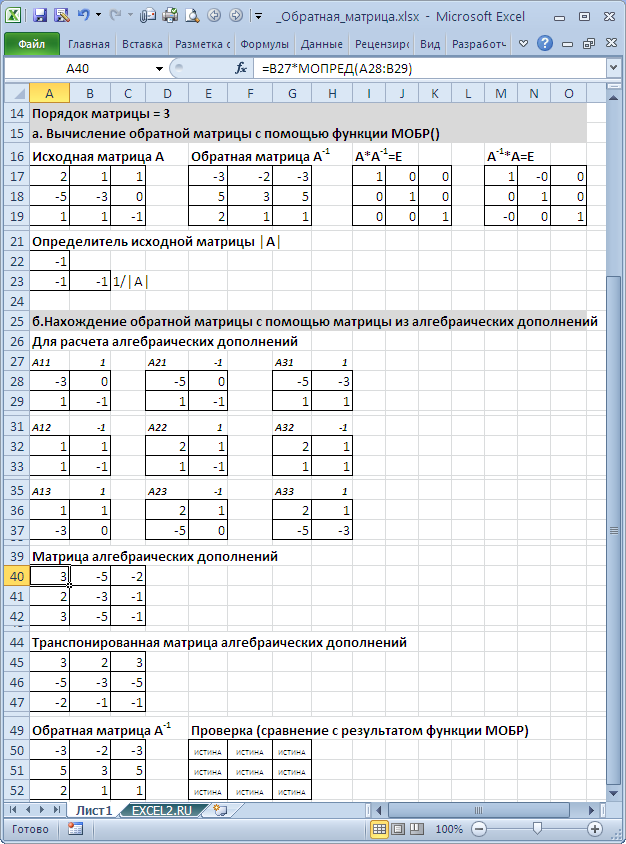
Порядок действий при вычислении обратной матрицы:
В качестве проверки можно перемножить исходную и обратную матрицы. В результате должна получиться единичная матрица.