Доказать примитивную рекурсивность функции

На этой странице вы найдете готовые примеры заданий по проверки примитивной рекурсивности функции .

Типовые задачи снабжены подробным решением, формулами, пояснениями. Используйте их, чтобы научиться решать подобные задачи или закажите решение своей работы нам.

Задачи и решения о рекурсивных функциях

Задача 1. Пользуясь определением примитивно рекурсивной функции, показать что числовая функция $f(x)$ примитивно рекурсивна. $f(x)=x!$

Задача 2. Доказать примитивную рекурсивность следующей функции $f(x,y)=xcdot y$.

Задача 3. Доказать, что заданная функция, определенная для натуральных аргументов и принимающая натуральные значения, является примитивно рекурсивной. $f(x,y)=x^y+x$.

Примитивно-рекурсивные функции

Введем базис простых операций:

• Константа 0
• Функция следования $x’=x+1$ (иногда обозначается $S(x)=x+1$)
• Функция проекции $I_m^n(x_1,x_2. x_n)=x_m$

Оператором суперпозиции (оператором подстановки) $S_m^n$ называется подстановка в функцию от $m$ переменных $m$ функций от $n$ одних и тех же переменных. Суперпозиция дает новую функцию от $n$ переменных.

Оператор примитивной рекурсии $R_n$ определяет $(n+1)$ – местную функцию $f$ через $n$ – местную функцию $g$ и $(n+2)$ – местную функцию $h$ так:

$$ f(x_1. x_n,0)=g(x_1. x_n),\ f(x_1. x_n,y+1)=h(x_1. x_n, y, f(x_1. x_n,y). $$

Эта пара равенств называется схемой примитивной рекурсии и обозначается, как

Данная схема определяет функцию $f$ рекурсивно не только через другие функции, но и через значения самой $f$ в предшествующих точках. Существенным в операторе примитивной рекурсии является то, что независимо от числа переменных в $f$ рекурсия ведется только по одной переменной $y$, а остальные $n$ переменных $x_1. x_n$ на момент применения схемы рекурсии зафиксированы и играют роль параметров.

Функция называется примитивно-рекурсивной, если она может быть получена из константы 0, функции $x’$ и функции $I_m^n$ с помощью конечного числа применений операторов суперпозиции и примитивной рекурсии.

Основные примитивно-рекурсивные функции: сложение $a+b$, умножение $ab$, возведение в степень $a^b$, симметрическая разность $|a-b|$.

Пусть заданы функции:

Функция f(x₁, . , x_n+1) получается из функций g и h с помощью операции примитивной рекурсии, если справедливы соотношения:

f(x₁, . . . , x_n, ) = g(x₁, . . . , x_n); (1)

f(x₁, . . . , x_n, y+1) = h(x₁, . . . , x_n, y, f(x₁, . . . , x_n, y)). (2)

Соотношения (1) и (2) называются схемой примитивной рекурсии. Соотношение (1) задает граничное условие, а соотношение (2) рекурсивно выражает значения функции f через другое значение этой функции.

Переменные x₁, . . . , x_n в схеме примитивной рекурсии представляют собой параметры. При этом допускается отсутствие параметров. В последнем случае функция g не имеет существенных переменных и является константой. Переменные x_n+1 и x_n+2 называются соответственно переменной рекурсии и переменной для рекурсивного вызова.

Предположим, что функции g и h являются вычислимыми. В этом случае функция f также является вычислимой.

Действительно, для нахождения значения f(x₁, . . . , x_n+1) можно воспользоваться следующей процедурой:

1. Вычислить значение f(x₁, . . . , x_n, ), используя алгоритм вычисления функции g и соотношение (1) схемы примитивной рекурсии.

2. Используя соотношение (2) и алгоритм вычисления функции h, можно последовательно вычислить значения

f(x₁, . . . , x_n, 1), . . . , f(x₁, . . . , x_n, x_n+1).

ОПРЕДЕЛЕНИЕ

Функции, получаемые из простейших функций с помощью конечного числа применений операций суперпозиции и примитивной рекурсии, называются примитивно-рекурсивными.

Из приведенного определения следует, что всякая примитивно-рекурсивная функция является всюду определенной функцией. Кроме того, все примитивно-рекурсивные функции вычислимы.

Упражнение. Показать, что если f(x₁, x₂) является примитивно-рекурсивной функцией, если она выражается через примитивно-рекурсивные функции g и h с помощью соотношений

f(, x) = g(x); (1)

f(y+1, x) = h(x, y, f(y, x)). (2)

Доказательство справедливости приведенного в упражнении утверждения обосновывать примитивную рекурсивность функций, определяемых рекурсивными схемами, в которых рекурсия ведется по произвольной переменной.

Рассмотрим примеры примитивно-рекурсивных функций.

1. Сумма f(x, у) = x + у задается следующей схемой примитивной рекурсии:

f(x, ) = (x);

f(x, у+1) = S(f(x, у)).

То есть f(x ,у) получается из элементарных функций g(x₁)= (x₁) и h(x₁, x₂, x₃) =S( ( x₁, x₂, x₃)) с помощью операции примитивной рекурсии и поэтому является примитивно-рекурсивной.

2. Произведение p(x, у) = x ´ у задается схемами:

p(x, ) = O(x);

p(x, у+1) = x+ p(x, у).

Здесь p выражается через функции O(x) и f( 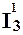(x₁, x₂, x₃), ( x₁, x₂, x₃)), где f – это примитивно-рекурсивная функция из предыдущего примера.

3. Экспонента e(x) = 2 x может быть задана соотношениями:

e() = S();

e(x+1) = 2×e(x).

Функции S((y)) и 2y – примитивно-рекурсивные. Поэтому функция e(x) также является примитивно-рекурсивной.

4. Функции sg(x) и (x), определяемые как:

sg(x) = и (x) = , задаются следующими схемами:

sg() = ; (x) = 1;

sg(x+1) = 1. (x+1) = .

5. Функция уменьшения на единицу d(x) = x – 1 определяется как:

d() = ;

d(x+1) = x.

6. Функция усеченного вычитания m(x, у) = x – у:

m (x, ) = x;

m (x, у+1) = d(m(x, у)).

Функции из примеров 5 и 6 являются аналогами арифметического вычитания для множества целых неотрицательных чисел. Такие функции по определению равны нулю, если вычитаемое больше уменьшаемого.

Используя приведенные ранее функции, можно доказывать примитивную рекурсивность и других известных числовых функций.

Например, рассмотрим функцию mod(x,y), принимающую значение, равное остатку от деления числа x на число y.

Для определенности положим, что при делении на нуль остаток всегда равен .

Определим mod(x, y) схемой:

mod(, y) = ; (1)

mod(x+1, y) = (mod(x, y)+1)× sg(y – (mod (x, y)+1)). (2)

Здесь рекурсия ведется по первой переменной.

В соотношении (2) реализовано очевидное свойство остатка от деления значения x+1 на y, которое можно выразить следующим соотношением:

mod(x+1, y) либо равен mod(x, y)+1, если mod(x, y)

Всякий алгоритм для любых исходных данных однозначно определяет некото- рый результат, если, конечно, этот результат существует для них. Поэтому каждо- му алгоритму соответствует функция, которая вычисляет этот результат. Поставим цель дать формальное определение произвольного алгоритма как функции, принад- лежащей некоторому специальным образом построенному классу функций. Для то- го, чтобы определение такого класса функций было строго формальным, необходимо выбрать способ его задания. Воспользуемся конструктивным методом определения и опишем некоторый класс функций с помощью рекурсивных определений. Основным свойством конструктивного подхода является то, что все множество исследуемых объектов (в данном случае функций ) строится из конечного числа исходных объек- тов — базиса — с помощью простых операций, эффективная выполнимость которых

достаточно очевидна. Операции над функциями в дальнейшем будем называть опе- раторами.

Рассмотрим сначала набор простейших функций, для которых с очевидностью

существуют алгоритмы их вычисления, а затем введем специальные операторы над числовыми функциями, с помощью которых можно будет из имеющихся функций получать новые функции.

В качестве простейших функций будем использовать следующие три функции:

1) 0(x1, . . . , xn) = 0 — нуль–функция,

2) s(x) = x + 1 — функция следования,

3) Im(x1, . . . , xn) = xm— функция выбора (или тождества).

m

Сразу отметим, что нуль–функция и функция выбора могут иметь разное число аргументов: 0n(x1, . . . , xn) и In(x1, . . . , xn).

Рассмотрим операторы, позволяющие конструировать новые функции из уже имеющихся. Введем в рассмотрение два оператора – оператор суперпозиции и опе- ратор примитивной рекурсии. Оператор суперпозиции из функций

строит новую функцию

m

Обозначим оператор суперпозиции через S(f, f1, . . . , fm) или, с явным указанием числа аргументов функций, Sn(f, f1, . . . , fm). Благодаря наличию функций выбора, стандартное представление суперпозиции с точным определением числа аргументов у всех функций f1, f2. fmне уменьшает возможностей самого оператора суперпо- зиции, т.к. любую подстановку функции в функцию можно выразить через оператор S и функцию I. Например, для трех функций

можно представить в виде стандартной суперпозиции h(f (I3(x, y, z)), g(x, y, z)).

Следует отметить, что при наличии нуль–функции и функции следования, а так- же оператора суперпозиции можно построить все множество натуральных чисел:

Рассмотрим оператор примитивной рекурсии. Известно, что рекурсия — это спо- соб вычисления значения функции в текущей точке через значение этой же функции в некоторых предыдущих точках. В зависимости от того, какие предшествующие точки используются при вычислении значения в текущей точке, рассматривают раз- личные схемы рекурсии.

Определение 2.1.Функция f (x1, . xn, y) получается оператором примитивной рекурсии из функций g(x1, . . . , xn) и h(x1, . . . , xn, y, z), если

Обозначим оператор примитивной рекурсии как R(g, h). Схема (2.2) называется схемой примитивной рекурсии. Например, при задании примитивно–рекурсивного описания функции одной переменной, схема примитивной рекурсии имеет вид:

где a — константа, принадлежащая множеству N .

Для того, чтобы в некоторой точке (x1, . . . , xn, y) вычислить значение функции, заданной оператором примитивной рекурсии, можно выполнить следующую конеч- ную последовательность вычислений:

Существенной характеристикой оператора примитивной рекурсии является такое его важнейшее свойство, что независимо от числа аргуменов функции f рекурсия ве- дется только по одному аргументу, остальные аргументы зафиксированы на момент применения рекурсии. Очевидно, что реализовать программное вычисление функ- ции, заданной оператором примитивной рекурсии, можно рекурсивным способом. Программа вычисления функции на языке Паскаль имеет вид:

function f(x1. xn,y: integer): integer; begin if y=0 then f:= g(x1. xn)

else f:= h(x1. xn,y-1,f(x1. xn,y-1))

Или на языке Си:

int f(int x1. int xn,int y)

return h(x1. xn,y-1,f(x1. xn,y-1));

Можно использовать итерационный метод вычисления этой же функции. Для этого в программе достаточно организовать цикл, который выполняется столько раз, какова глубина вызова рекурсивной функции.

function f(x1. xn,y: integer): integer; var t,i: integer;

for i:=0 to y-1 do t:= h(x1. xn, i, t); f:=t;

Или соответственно на языке Си:

int f(int x1. int xn,int y)

for ( int i=0; i 0

Другая знаковая функция sg(x) возвращает отрицание знака:

Как уже отмечалось, суперпозицию функции f (x, y) и функций произвольного ви- да, не содержащих f (x, y), всегда можно представить в стандартной форме (2.2), если воспользоваться функцией выбора. Поэтому, если для некоторой функции f (x, y) мы провели доказательство ее примитивной рекурсивности с помощью оператора при- митивной рекурсии и для выражения f (x, y + 1) получили не стандартную форму су- перпозиции функции f (x, y) и известных примитивно–рекурсивных функций, то мы знаем, что получить стандартную форму (2.2) мы всегда можем. Поэтому в дальней- шем мы не всегда будем доводить процесс доказательства до конечной суперпозиции в стандартном виде (2.2).

Оператор минимизации

Вернемся к начальной цели, которую мы поставили — дать формальное опре- деление алгоритма как функции, принадлежащей некоторому конструктивно опре- деленному классу функций. Возможно, что определение примитивно–рекурсивных функций будет удовлетворять этой цели. Однако сначала надо практически убедить- ся в том, что частный случай алгоритмов — программы для ЭВМ — можно предста- вить примитивно–рекурсивными функциями. Заданные в определении примитивно– рекурсивных функций средства их конструирования позволяют использовать для на- писания алгоритмов простейшие функции, оператор суперпозиции и оператор прими- тивной рекурсии. Если рассматривать программную реализацию этих конструктив- ных элементов, то простейшие функции соответствуют некоторому базовому набору операций языка программирования, оператор суперпозиции — последовательному выполнению действий, а оператор примитивной рекурсии — рекурсивной процедуре или оператору цикла типа "for". Рассмотрим достаточность этих средств для кон- струирования любого алгоритма. Сначала введем в рассмотрение новый оператор, представляющий аналог оператора цикла типа "while". Поскольку такой цикл вы- полняется многократно при истинности некоторого условия, необходимо рассматри- вать предикаты, определяющие такие условия. Любой предикат принимает значения "ложь" и "истина с которыми нельзя производить арифметических действий. Для

того, чтобы представить значение предиката натуральным числом, введем понятие характеристической функции предиката

Кстати, при реализации логических переменных в программах для ЭВМ также обычно используются именно числа 0 и 1 для машинного представления значений "ложь" и "истина".

Теперь можно дать определение специального оператора, выполняющего цикл вычислений по некоторому условию.

Определение 2.3.Функция f (x1, . . . , xn) получается оператором минимизации из предиката P (x1, . . . , xn, z), если в любой точке (x1, x2, . xn) значением функции f (x1, . . . , xn) является минимальное значение z, обращающее предикат P (x1, . . . , xn, z)

в истину. Оператор минимизации имеет обозначение

Для того, чтобы для любого предиката P (x1, . . . , xn, z) найти минимальное зна- чение z, обращающее P (x1, . . . , xn, z) в истину, нужно последовательно перебирать значения z = 0, 1, 2, . . Вычисление значения функции, заданной с помощью опера- тора минимизации, можно программно реализовать следующим образом:

int f(int x1. int xn)

while (P(x1. xn,z)==0) z++; return z;

Пример.Пусть f (x, y) = µz(2∗x+z = y+1). Предикат P (x, y, z) = (2∗x+z = y+1) является примитивно–рекурсивным, т.к. его характеристическая функция является суперпозицией примитивно–рекурсивных функций и равна

Вычислим значение f (1, 5):

z = 0,	P (1, 5, 0) =	Ложь,
z = 1, . . . z = 4,	P (1, 5, 1) = P (1, 5, 4) =	Ложь, Истина.

Тогда f (1, 5) = 4. Рассмотрим вычисление f (5, 1). В этой точке функция не опре- делена, т.к. P (5, 1, z) = "Ложь"для любого значения z ∈ N .

Полученный пример показывает, что с помощью оператора минимизации из при- митивно–рекурсивных функций можно получить не всюду определенные функции, поэтому оператор минимизации выводит из класса примитивно–рекурсивных функ- ций. Попробуем сделать так, чтобы остаться внутри класса примитивно–рекурсивных функций, но оставить возможность использования циклов типа "while". Для этого достаточно при определении оператора минимизации ввести ограничение на измене- ние переменной z так, чтобы цикл всегда завершался после некоторого числа шагов. В общем случае такое ограничение должно являться функцией свободных перемен- ных x1, x2. xn.

Папиллярные узоры пальцев рук – маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ – конструкции, предназначен­ные для поддерживания проводов на необходимой высоте над землей, водой.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого.