Даны три последовательные вершины параллелограмма А(-2;1),В(1;3),С(4;0). Найти четвертую его координату D. Система координат аффинная.
Векторы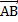 
и 
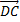равны, значит, равны их координаты ( коэффициенты линейной комбинации):
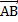= <3;2>, 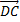=<4-x;-y>; 
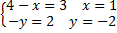. Значит, D(1;-2).
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Учись учиться, не учась! 10425 – 
| 7910 – 
или читать все.
78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Даны три последовательные вершины параллелограмма . Найти:
а) уравнение стороны
б) уравнение высоты, проведенной из вершины на сторону , длину этой высоты;
в) уравнение диагонали
г) площадь параллелограмма;
д) угол между диагоналями параллелограмма.
Версия системы:
7.78 (18.11.2019)
JS-v.1.34 | CSS-v.3.35
Общие новости:
28.04.2019, 09:13
Последний вопрос:
19.11.2019, 17:08
Всего: 151008
Последний ответ:
19.11.2019, 19:03
Всего: 259429
Последняя рассылка:
19.11.2019, 16:15
РАЗДЕЛ • Математика
Консультации и решение задач по алгебре, геометрии, анализу, дискретной математике.
[администратор рассылки: Гордиенко Андрей Владимирович (Профессионал)]
Лучшие эксперты в этом разделе
|
Коцюрбенко Алексей Владимирович Статус: Модератор Рейтинг: 1361 |
Лысков Игорь Витальевич Статус: Старший модератор Рейтинг: 154 |
kovalenina Статус: Практикант Рейтинг: 128 |
| Перейти к консультации №: |
Здравствуйте, уважаемые эксперты! Прошу Вас ответить на следующий вопрос:
Даны три последовательные вершины параллелограмма A(2;-3), B(6;-3), C(5;-5)
Найти:
– Уравнение стороны AD
– Уравнение Высоты, опущенной из вершины В на сторону AD, длину этой высоты
– Уравнение диагонали BD
– Площадь параллелограмма
– Угол между диагоналями параллелограмма
Состояние: Консультация закрыта
Здравствуйте, Посетитель – 344328!
Построив рисунок, легко находим, что точка D имеет координаты (1; -5)
Найдем уравнение прямой, проходящей через точки A и D:
Используем формулу (y-y1)/(y2-y1) = (x-x1)/(x2-x1)
(y+3)/(-5+2) = (x-2)/(1-2) ⇒ y = 2x – 7
Об уравнении прямой y = kx+b, о которой известно, что прямая ⊥ известной y = k1x + b1,
можно сказать, что k = – 1/k1, а b нахотится из условия прохождения через известную точку.
Итак, имеем k1 = 2. Тогда k = -1/2. Т.е. имеем уравнение y = -1/2 x + b
Перпендикуляр проходит через точку B, значит -3 = -1/2 * 6 + b, откуда b = 0
Значит, уравние высоты BE имеет вид y = -1/2 x
Найдем координаты точки пересечения AD (y = 2x – 7) и высоты BE (y = -1/2 x)
2x – 7 = -1/2 x ⇒ x = 14/5, из уравнения y = -1/2 x находим y = -7/5
Т.о. имеем точку E(14/5; -7/5)
Тогда |BE| = √((6-14/5) 2 + (-3+7/5) 2 ) = (8/5)√5 ≈3.58
Уравнение диагонали BD:
(y+3)/(-5+3) = (x-6)/(1-6) ⇒ y = 2/5 x – 27/5
Площадь S = |AD||BE| =(√((1-2) 2 + (-3+5) 2 )) (8/5)√5 = √5 (8/5)√5 = 8
Перед тем, как будем искать угол между диагоналями, найдем уравнение второй диагонали AC
(y+3)/(-5+3) = (x-2)/(5-2) ⇒ y = -2/3 x – 5/3
Имеем тангенсы двух углов tg(α) = 2/5, tg(β) = -2/3
Искомый угол γ равен разности α – β
Воспользуемся формулой tg( α – β ) = (tg( α ) – tg( β )) / (1 + tg( α ) * tg( β ))
tg( γ ) = (2/5 + 2/3)/(1 – 2/5 * 2/3) = 16/11
γ = arctg(16/11) ≈ 55.49°
0 
Отправлять сообщения
модераторам могут
только участники портала.
ВОЙТИ НА ПОРТАЛ »
регистрация »
“>