- Сложение и вычитание
- Умножение
- Что сначала – умножение или сложение?
- Деление
- Скобки
- «Вишенка на торте»
- «Совсем вишня»
- Наблюдение за изменением значения выражения от порядка выполнения арифметических действий
- Порядок выполнения арифметических действий в выражениях без скобок
- Порядок выполнения арифметических действий в выражениях со скобками
- Правило выполнения арифметических действий в выражениях без скобок и со скобками
- Выполнение тренировочных заданий на изученное правило
Вот вам очень простой математический пример:
8 / 2(2 + 2)
Вы удивитесь, но большинство людей не смогут правильно это посчитать. Посчитайте сами и потом смотрите правильный ответ:
В интернете много споров про такие примеры, поэтому мы решили разобраться, какие ошибки совершают чаще всего и почему многие считают неправильно. Для решения нам понадобятся три математических правила:
- То, что в скобках, выполняется в первую очередь. Если скобок несколько, они выполняются слева направо.
- При отсутствии скобок математические действия выполняются слева направо, сначала умножение и деление, потом — сложение и вычитание.
- Между множителем и скобкой (или двумя скобками) может опускаться знак умножения.
Разберём подробнее, что это значит в нашем случае.
1. То, что в скобках, выполняется в первую очередь. То есть в нашем примере, вне зависимости от чего угодно, сначала схлопнутся скобки:
8 / 2(2 + 2) → 8 / 2(4)
2. Между числом и скобкой можно опустить знак умножения. У нас перед скобкой двойка, то есть можно сделать такую замену:
3. Математические действия при отсутствии скобок выполняются слева направо: как при чтении, сначала умножение и деление, потом — сложение и вычитание. Умножение и деление имеют одинаковый приоритет. Нет такого, что сначала всегда делается умножение, затем деление, или наоборот. Со сложением и вычитанием то же самое.
Некоторые считают, что раз множители были написаны близко друг к другу (когда там стояли скобки), то оно выполняется в первую очередь, ссылаясь при этом на разные методические пособия. На самом деле это не так, и нет такого скрытого умножения, которое имеет приоритет над другим умножением или делением. Это такое же умножение, как и остальные, и оно делается в общем порядке — как и принято во всём математическом мире.
Получается, что нам сначала надо сложить 2 + 2 в скобках, потом 8 разделить на 2, и полученный результат умножить на то, что в скобках:
8 / 2 × (2 + 2) = 8 / 2 × 4 = 4 × 4 = 16
Кстати, если на айфоне записать это выражение точно так же, как в условии, телефон тоже даст правильный ответ.
А инженерный калькулятор на Windows 10 так записывать не умеет и пропускает первую двойку-множитель. Попробуйте сами 🙂
Тут в тред врываются математики и с воплями «Шустеф!» поясняют криком:
«В АЛГЕБРЕ ТОТ ЖЕ ПОРЯДОК ДЕЙСТВИЙ, ЧТО И В АРИФМЕТИКЕ, но есть исключение: в алгебре знак умножения связывает компоненты действия сильнее, чем знак деления, поэтому знак умножения опускается. Например, a:b·c= a: (b·c)».
Этот текст из «Методики преподавания алгебры», курс лекций, Шустеф М. Ф., 1967 год. (стр. 43)
Раз в спорном примере знак умножения опущен, то спорный пример алгебраический, а значит, сначала умножаем 2 на 4, а потом 8 делим на 8!
А вот как на это отвечают те, кто действительно в теме и не ленится полностью посмотреть первоисточник:
«Для устранения недоразумений В. Л. Гончаров указывает, что предпочтительнее пользоваться в качестве знака деления чертой и ставить скобки [87]. П. С. Александров и А. Н. Колмогоров [59] предложили изменить порядок действий в арифметике и решать, например, так: 80:20×2=80:40=2 вместо обычного: 80:20×2=4×2=8. Однако это предложение не нашло поддержки».
Если апеллировать к Фриде Максовне Шустеф, то выходит, что:
- В. Л. Гончаров говорит так: «Ребята, используйте черту и ставьте скобки, чтобы ни у кого не было вопросов про приоритет».
- Если у нас всё же битва арифметики и алгебры, то, по П. С. Александрову и А. Н. Колмогорову, пример нужно решать слева направо, как обычно. Они, конечно, предложили решать такое по-другому, но научное сообщество их не поддержало.
Самое интересное, что дальше в примерах Фрида Максовна пользуется как раз правильным порядком действий, объясняя решение. Даже там, где есть умножение на скобку с опущенным знаком, она выполняет действия слева направо.
С самого начала следует напомнить, чтобы потом не путаться: есть цифры – их 10. От 0 до 9. Есть числа, и они состоят их цифр. Чисел бесконечно много. Точно больше, чем звезд на небе.
Математическое выражение − это записанное с помощью математических символов наставление, какие действия нужно произвести с числами, чтобы получить результат. Не «выйти» на искомый результат, как в статистике, а узнать, сколько их точно было. А вот чего и когда было − уже не входит в сферу интересов арифметики. При этом важно не ошибиться в последовательности действий, что сначала – сложение или умножение? Выражение в школе иногда называют «пример».
 Вам будет интересно: Консилиум – это не приговор
Вам будет интересно: Консилиум – это не приговор

Сложение и вычитание
Какие же действия можно произвести с числами? Есть два базовых. Это сложение и вычитание. Все остальные действия построены на этих двух.
Самое простое человеческое действие: взять две кучки камней и смешать их в одну. Это и есть сложение. Для того чтобы получить результат такого действия, можно даже не знать, что такое сложение. Достаточно просто взять кучку камней у Пети и кучку камней у Васи. Сложить все вместе, посчитать все заново. Новый результат последовательного счета камней из новой кучки − это и есть сумма.
 Вам будет интересно: Остеоны или система Гаверсова
Вам будет интересно: Остеоны или система Гаверсова
Точно так же можно не знать, что такое вычитание, просто взять и разделить кучу камней на две части или забрать из кучи какое-то количество камней. Вот и останется в куче то, что называется разностью. Забрать можно только то, что есть в куче. Кредит и прочие экономические термины в данной статье не рассматриваются.
Чтобы не пересчитывать каждый раз камни, ведь бывает, что их много и они тяжелые, придумали математические действия: сложение и вычитание. И для этих действий придумали технику вычислений.

Сумма двух любых цифр тупо заучиваются без всякой техники. 2 плюс 5 равно семь. Посчитать можно на счетных палочках, камнях, рыбьих головах – результат одинаковый. Положить сначала 2 палочки, потом 5, а потом посчитать все вместе. Другого способа нет.
Те, кто поумнее, обычно это кассиры и студенты, заучивают больше, не только сумму двух цифр, но и суммы чисел. Но самое главное, они могут складывать числа в уме, используя разные методики. Это называется навыком устного счета.
 Вам будет интересно: Тореро – это. Значение слова
Вам будет интересно: Тореро – это. Значение слова
Для сложения чисел, состоящих из десятков, сотен, тысяч и еще больших разрядов, используют специальные техники − сложение столбиком или калькулятор. С калькулятором можно не уметь складывать даже цифры, да и читать дальше не нужно.
Сложение столбиком − это метод, который позволяет складывать большие (многоразрядные) числа, выучив только результаты сложения цифр. При сложении столбиком последовательно складываются соответствующие десятичные разряды двух чисел (то есть фактически две цифры), если результат сложения двух цифр превышает 10, то учитывается только последний разряд этой суммы – единицы числа, а к сумме следующих разрядов добавляется 1.
Умножение
Математики любят группировать похожие действия для упрощения расчетов. Так и операция умножения является группировкой одинаковых действий – сложения одинаковых чисел. Любое произведение N x M − есть N операций сложения чисел M. Это всего лишь форма записи сложения одинаковых слагаемых.
Для вычисления произведения используется такой же метод – сначала тупо заучивается таблица умножения цифр друг на друга, а потом применяется метод поразрядного умножения, что называется «в столбик».

Что сначала – умножение или сложение?
Любое математическое выражение – это фактически запись учетчика «с полей» о результатах каких-либо действий. Допустим, сбора урожая помидоров:
- 5 взрослых работников собрали по 500 помидоров каждый и выполнили норму.
- 2 школьников не ходили на уроки математики и помогали взрослым: собрали по 50 помидоров, норму не выполнили, съели 30 помидоров, надкусили и испортили еще 60 помидоров, 70 помидоров было изъято из карманов помощников. Зачем брали с собой их в поле – непонятно.
Все помидоры сдавали учетчику, он укладывал их по кучкам.
Запишем результат «сбора» урожая в виде выражения:
- 500 + 500 + 500 + 500 + 500 – это кучки взрослых работников;
- 50 + 50 – это кучки малолетних работников;
- 70 – изъято из карманов школьников (испорченное и надкусанное в зачет результата не идет).
Получаем пример для школы, запись учетчика результатов работы:
500 + 500 +500 +500 +500 + 50 +50 + 70 =?;
Здесь можно применить группировку: 5 кучек по 500 помидоров − это можно записать через операцию умножения: 5 ∙ 500.
Две кучки по 50 – это тоже можно записать через умножение.
И одна кучка 70 помидоров.
5 ∙ 500 + 2 ∙ 50 + 1 ∙ 70 =?
И что делать в примере сначала − умножение или сложение? Так вот, складывать можно только помидоры. Нельзя сложить 500 помидоров и 2 кучки. Они не складываются. Поэтому сначала нужно всегда все записи привести к базовым операциям сложения, то есть в первую очередь вычислить все операции группировки-умножения. Совсем простыми словами – сначала выполняется умножение, а сложение уже потом. Если умножить 5 кучек по 500 помидоров каждая, то получится 2500 помидоров. А дальше их уже можно складывать с помидорами из других кучек.
2500 + 100 + 70 = 2 670
При изучении ребенком математики нужно донести до него, что это инструмент, используемый в повседневной жизни. Математические выражения являются, по сути (в самом простом варианте начальной школы), складскими записями о количестве товаров, денег (очень легко воспринимается школьниками), других предметов.
Соответственно, любое произведение – это сумма содержимого некоторого количества одинаковых емкостей, ящиков, кучек, содержащих одинаковое количество предметов. И что сначала умножение, а сложение потом, то есть сначала начала вычислить общее количество предметов, а затем уже складывать их между собой.
Деление
Операция деления отдельно не рассматривается, она обратная умножению. Нужно что-то распределить по коробкам, так, чтобы во всех коробках было одинаковое заданное количество предметов. Самый прямой аналог в жизни – это фасовка.

Скобки
Большое значение в решении примеров имеют скобки. Скобки в арифметике – математический знак, используемый для регулирования последовательности вычислений в выражении (примере).
Умножение и деление имеют приоритет выше, чем сложение и вычитание. А скобки имеют приоритет выше, чем умножение и деление.
Все, что записано в скобках, вычисляется в первую очередь. Если скобки вложенные, то сначала вычисляется выражение во внутренних скобках. И это непреложное правило. Как только выражение в скобках вычислено, скобки пропадают, а на их месте возникает число. Варианты раскрытия скобок с неизвестными здесь не рассматриваются. Так делают до тех пор, пока все они не исчезнут из выражения.
- Это как коробочки с конфетами в большом мешке. Сначала нужно раскрыть все коробочки и ссыпать в большой мешок: (25 – 5 ) = 20. Пять конфет из коробочки сразу заслали отличнице Люде, которая приболела и в празднике не участвует. Остальные конфеты − в мешок!
- Потом связать конфеты в пучки по 5 штук: 20 : 5 = 4.
- Потом добавить в мешок еще 2 пучка конфет, чтобы можно было поделить на троих детей без драки. Признаки деления на 3 в данной статье не рассматриваются.
(20 : 5 + 2) : 3 = (4 +2) : 3 = 6 : 3 = 2
Итого: трем детям по два пучка конфет (по пучку в руку), по 5 конфет в пучке.
Если вычислить первые скобки в выражении и переписать все заново, пример станет короче. Метод не быстрый, с большим расходом бумаги, зато удивительно эффективный. Заодно тренирует внимательность при переписывании. Пример приводится к виду, когда остается только один вопрос, сначала умножение или сложение без скобок. То есть к такому виду, когда скобок уже и нет. Но ответ на этот вопрос уже есть, и нет смысла обсуждать, что идет сначала – умножение или сложение.
«Вишенка на торте»
И напоследок. К математическому выражению не применимы правила русского языка – читать и выполнять слева направо:
Это простенький пример может довести до истерики ребенка или испортить вечер его маме. Потому что именной ей придется объяснять второкласснику, что бывают отрицательные числа. Или рушить авторитет «МарьиВановны», которая сказала, что: «Нужно слева направо и по порядку».
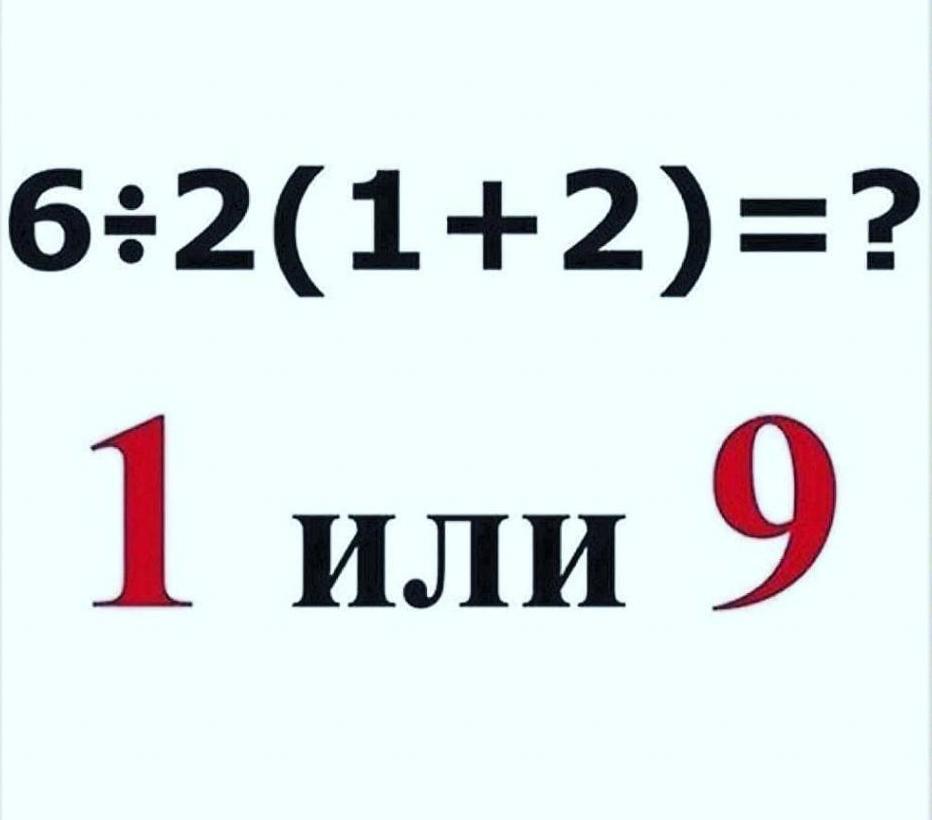
«Совсем вишня»
В Сети гуляет пример, вызывающий затруднения у взрослых дяденек и тетенек. Он не совсем по рассматриваемой теме, что сначала – умножение или сложение. Он вроде как про то, что сначала выполняете действие в скобках.
От перестановки слагаемых сумма не изменяется, от перестановки множителей тоже. Нужно просто записывать выражение так, чтобы не было потом мучительно стыдно.
6 : 2 ∙ (1+2) = 6 ∙ ½ ∙ (1+2) = 6 ∙ ½ ∙ 3 = 3 ∙ 3 = 9
На данном уроке подробно рассмотрен порядок выполнения арифметических действий в выражениях без скобок и со скобками. Учащимся предоставляется возможность в ходе выполнения заданий определить, зависит ли значение выражений от порядка выполнения арифметических действий, узнать отличается ли порядок арифметических действий в выражениях без скобок и со скобками, потренироваться в применении изученного правила, найти и исправить ошибки, допущенные при определении порядка действий.
Наблюдение за изменением значения выражения от порядка выполнения арифметических действий
В жизни мы постоянно выполняем какие-либо действия: гуляем, учимся, читаем, пишем, считаем, улыбаемся, ссоримся и миримся. Эти действия мы выполняем в разном порядке. Иногда их можно поменять местами, а иногда нет. Например, собираясь утром в школу, можно сначала сделать зарядку, затем заправить постель, а можно наоборот. Но нельзя сначала уйти в школу, а потом надеть одежду.
А в математике обязательно ли выполнять арифметические действия в определенном порядке?
Сравним выражения:
8-3+4 и 8-3+4
Видим, что оба выражения совершенно одинаковы.
Выполним действия в одном выражения слева направо, а в другом справа налево. Числами можно проставить порядок выполнения действий (рис. 1).

Рис. 1. Порядок действий
В первом выражении мы сначала выполним действие вычитания, а затем к результату прибавим число 4.
Во втором выражении сначала найдем значение суммы, а потом из 8 вычтем полученный результат 7.
Видим, что значения выражений получаются разные.
Сделаем вывод: порядок выполнения арифметических действий менять нельзя.
Порядок выполнения арифметических действий в выражениях без скобок
Узнаем правило выполнения арифметических действий в выражениях без скобок.
Если в выражение без скобок входят только сложение и вычитание или только умножение и деление, то действия выполняют в том порядке, в каком они написаны.
В этом выражении имеются только действия сложения и вычитания. Эти действия называют действиями первой ступени.
Выполняем действия слева направо по порядку (рис. 2).

Рис. 2. Порядок действий
Рассмотрим второе выражение
В этом выражении имеются только действия умножения и деления – это действия второй ступени.
Выполняем действия слева направо по порядку (рис. 3).

Рис. 3. Порядок действий
В каком порядке выполняются арифметические действия, если в выражении имеются не только действия сложения и вычитания, но и умножения и деления?
Если в выражение без скобок входят не только действия сложения и вычитания, но и умножения и деления, или оба этих действия, то сначала выполняют по порядку (слева направо) умножение и деление, а затем сложение и вычитание.
Рассуждаем так. В этом выражении имеются действия сложения и вычитания, умножения и деления. Действуем по правилу. Сначала выполняем по порядку (слева направо) умножение и деление, а затем сложение и вычитание. Расставим порядок действий.
Вычислим значение выражения.
Порядок выполнения арифметических действий в выражениях со скобками
В каком порядке выполняются арифметические действия, если в выражении имеются скобки?
Если в выражении имеются скобки, то сначала вычисляют значение выражений в скобках.
Мы видим, что в этом выражении имеется действие в скобках, значит, это действие выполним первым, затем по порядку умножение и сложение. Расставим порядок действий.
Вычислим значение выражения.
Правило выполнения арифметических действий в выражениях без скобок и со скобками
Как нужно рассуждать, чтобы правильно установить порядок арифметических действий в числовом выражении?
Прежде чем приступить к вычислениям, надо рассмотреть выражение (выяснить, есть ли в нём скобки, какие действия в нём имеются) и только после этого выполнять действия в следующем порядке:
1. действия, записанные в скобках;
2. умножение и деление;
3. сложение и вычитание.
Схема поможет запомнить это несложное правило (рис. 4).

Рис. 4. Порядок действий
Выполнение тренировочных заданий на изученное правило
Рассмотрим выражения, установим порядок действий и выполним вычисления.
Будем действовать по правилу. В выражении 43 – (20 – 7) +15 имеются действия в скобках, а также действия сложения и вычитания. Установим порядок действий. Первым действием выполним действие в скобках, а затем по порядку слева направо вычитание и сложение.
43 – (20 – 7) +15 =43 – 13 +15 = 30 + 15 = 45
В выражении 32 + 9 * (19 – 16) имеются действия в скобках, а также действия умножения и сложения. По правилу первым выполним действие в скобках, затем умножение (число 9 умножаем на результат, полученный при вычитании) и сложение.
32 + 9 * (19 – 16) =32 + 9 * 3 = 32 + 27 = 59
В выражении 2*9-18:3 отсутствуют скобки, зато имеются действия умножения, деления и вычитания. Действуем по правилу. Сначала выполним слева направо умножение и деление, а затем от результата, полученного при умножении, вычтем результат, полученный при делении. То есть первое действие – умножение, второе – деление, третье – вычитание.
Узнаем, правильно ли определен порядок действий в следующих выражениях.
В этом выражении скобки отсутствуют, значит, сначала выполняем слева направо умножение или деление, затем сложение или вычитание. В данном выражении первое действие – деление, второе – умножение. Третье действие должно быть сложение, четвертое – вычитание. Вывод: порядок действий определен верно.
Найдем значение данного выражения.
Во втором выражении имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – деление, третье – сложение. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
В этом выражении также имеются скобки, значит, сначала выполняем действие в скобках, затем слева направо умножение или деление, сложение или вычитание. Проверяем: первое действие – в скобках, второе – умножение, третье – вычитание. Вывод: порядок действий определен неверно. Исправим ошибки, найдем значение выражения.
Расставим порядок действий в выражении, используя изученное правило (рис. 5).

Рис. 5. Порядок действий
Мы не видим числовых значений, поэтому не сможем найти значение выражений, однако потренируемся применять изученное правило.
Действуем по алгоритму.
В первом выражении имеются скобки, значит, первое действие в скобках. Затем слева направо умножение и деление, потом слева направо вычитание и сложение.
Во втором выражении также имеются скобки, значит, первое действие выполняем в скобках. После этого слева направо умножение и деление, после этого – вычитание.
Проверим себя (рис. 6).

Рис. 6. Порядок действий
Сегодня на уроке мы познакомились с правилом порядка выполнения действий в выражениях без скобок и со скобками.
Список литературы
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 1. – М.: «Просвещение», 2012.
- М.И. Моро, М.А. Бантова и др. Математика: Учебник. 3 класс: в 2-х частях, часть 2. – М.: «Просвещение», 2012.
- М.И. Моро. Уроки математики: Методические рекомендации для учителя. 3 класс. – М.: Просвещение, 2012.
- Нормативно-правовой документ. Контроль и оценка результатов обучения. – М.: «Просвещение», 2011.
- «Школа России»: Программы для начальной школы. – М.: «Просвещение», 2011.
- С.И. Волкова. Математика: Проверочные работы. 3 класс. – М.: Просвещение, 2012.
- В.Н. Рудницкая. Тесты. – М.: «Экзамен», 2012.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
Домашнее задание
1. Определи порядок действий в данных выражениях. Найди значение выражений.
2. Определи, в каком выражении такой порядок выполнения действий:
1. умножение; 2. деление;. 3. сложение; 4. вычитание; 5. сложение. Найди значение данного выражения.
3. Составь три выражения, в которых такой порядок выполнения действий:
1. умножение; 2. сложение; 3. вычитание
1. сложение; 2. вычитание; 3. сложение
1. умножение; 2. деление; 3. сложение
Найди значение этих выражений.
Если вы нашли ошибку или неработающую ссылку, пожалуйста, сообщите нам – сделайте свой вклад в развитие проекта. 

